图论与算法(5)图的广度优先遍历应用
1. 广度优先遍历
1.1 树的广度优先遍历
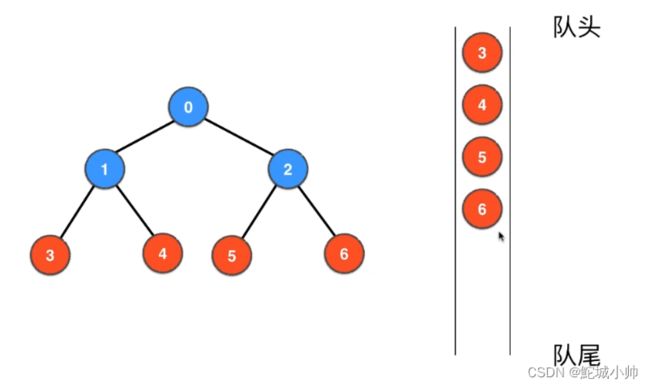
树的广度优先遍历(Breadth-First Traversal),也称为层次遍历,是一种按层次顺序逐级访问树节点的遍历方式。在广度优先遍历中,先访问树的根节点,然后按照从上到下、从左到右的顺序逐层访问树的节点。
首先将树的根节点入队列,然后循环执行以下操作:出队列一个节点,对该节点进行处理,然后将该节点的所有子节点按顺序入队列。通过不断出队列和入队列的操作,可以按照层次顺序逐级遍历树的节点,直到队列为空。
广度优先遍历保证了在访问某一层节点之前,先访问上一层的所有节点。这种遍历方式通常适用于需要按层次分析树结构的情况,比如求解最短路径、最小生成树等问题。
值得注意的是,广度优先遍历仅适用于无向树或有向无环图。对于有向有环图,由于存在环路,可能导致遍历陷入死循环。
1.2 图的广度优先遍历
图的广度优先遍历(Breadth-First Traversal),也称为宽度优先搜索(BFS),是一种遍历图的算法。在广度优先遍历中,从图中的某个起始节点开始,逐层遍历图的节点,先访问当前节点的所有邻接节点,然后再按顺序访问邻接节点的邻接节点,以此类推,直到遍历完图中所有可达节点。
下面是图的广度优先遍历的代码:
package BFS;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
/**
* 图的广度优先遍历(BFS)
* @author wushaopei
* @create 2023-06-05 10:04
*/
public class GraphBFS {
private Graph G; // 图对象
private boolean[] visited; // 记录顶点是否访问过
private List order; // 记录顶点的遍历顺序
public GraphBFS(Graph G) {
this.G = G;
visited = new boolean[G.V()];
order = new ArrayList<>(G.V());
for (int v = 0; v < G.V(); v++) {
if (!visited[v]) {
bfs(v); // 对未访问过的顶点进行BFS
}
}
}
private void bfs(int s) {
Queue queue = new LinkedList<>(); // 创建队列用于存储待访问顶点
queue.add(s); // 将起始顶点入队
visited[s] = true; // 标记起始顶点为已访问
while (!queue.isEmpty()) { // 当队列不为空时,继续遍历
int v = queue.remove(); // 出队一个顶点v
order.add(v); // 将v添加到遍历顺序中
for (int w : G.adj(v)) { // 遍历v的邻接顶点w
if (!visited[w]) { // 如果w未被访问过
visited[w] = true; // 标记w为已访问
order.add(w); // 将w入队
}
}
}
}
public Iterable order() {
return order; // 返回顶点的遍历顺序
}
public static void main(String[] args) {
Graph graph = new Graph("cc.txt");
GraphBFS graphBFS = new GraphBFS(graph);
System.out.println(graphBFS.order());
}
}
在上述代码中,使用了一个队列来辅助实现广度优先遍历。首先将起始节点入队列,然后循环执行以下操作:出队列一个节点,对该节点进行处理,并将其标记为已访问,然后将该节点的未访问过的邻接节点按顺序入队列。通过不断出队列和入队列的操作,可以按照广度优先的顺序遍历图中的节点。
广度优先遍历的特点是从起始节点开始逐层向外扩展,先访问离起始节点最近的节点,再访问稍远的节点,直到遍历到图中所有可达节点。这种遍历方式可以用于求解最短路径、连通性问题等。
值得注意的是,在处理图的广度优先遍历时,需要使用额外的数据结构来记录已访问的节点,以防止重复访问和陷入循环。常用的数据结构有集合(Set)或标记数组等。
2. 路径问题
路径问题
如果两个顶点在同一个联通分量中,那么它们之间一定存在路径。联通分量是指图中的一组顶点,这些顶点之间可以相互连通,通过边进行路径的传递。
单源路径问题是指在给定的图中,找到从单个源顶点到其他所有顶点的路径。下面是使用广度优先搜索(DFS)来解决单源路径问题的步骤:
package BFS;
/**
* @author wushaopei
* @create 2023-06-05 10:35
*/
import java.util.*;
/**
* 图的广度优先遍历(BFS)
* @author wushaopei
* @create 2023-06-05 10:04
*/
/**
* 图的单源路径问题,使用广度优先遍历(BFS)求解
*/
public class SingleSourcePath {
private Graph G; // 图对象
private boolean[] visited; // 记录顶点是否访问过
private int s; // 源顶点
private int[] pre; // 记录顶点在路径中的前一个顶点
public SingleSourcePath(Graph G, int s) {
this.G = G;
this.s = s;
visited = new boolean[G.V()]; // 初始化visited数组,默认所有顶点未访问
pre = new int[G.V()]; // 初始化pre数组,默认所有顶点前一个顶点为-1
for (int v = 0; v < G.V(); v++) {
pre[v] = -1;
}
bfs(s); // 从源顶点s开始进行BFS遍历
}
private void bfs(int s) {
Queue queue = new LinkedList<>(); // 创建队列用于存储待访问顶点
queue.add(s); // 将源顶点s入队
visited[s] = true; // 标记源顶点s为已访问
while (!queue.isEmpty()) { // 当队列不为空时,继续遍历
int v = queue.poll(); // 出队一个顶点v
for (int w : G.adj(v)) { // 遍历顶点v的邻接顶点w
if (!visited[w]) { // 如果w未被访问过
queue.add(w); // 将w入队
visited[w] = true; // 标记w为已访问
pre[w] = v; // 设置w在路径中的前一个顶点为v
}
}
}
}
public boolean isConnectedTo(int t) {
G.validateVertex(t); // 验证目标顶点t是否合法
return visited[t]; // 返回目标顶点t是否与源顶点s相连
}
public Iterable path(int t) {
List res = new ArrayList<>();
if (!isConnectedTo(t)) return res; // 若目标顶点t与源顶点s不相连,则返回空路径
int cur = t;
while (cur != s) {
res.add(cur); // 将当前顶点加入路径中
cur = pre[cur]; // 更新当前顶点为其前一个顶点
}
res.add(s); // 将源顶点s加入路径中
Collections.reverse(res); // 反转路径列表,得到从源顶点s到目标顶点t的路径
return res; // 返回路径列表
}
public static void main(String[] args) {
Graph graph = new Graph("cc.txt");
SingleSourcePath singleSourcePath = new SingleSourcePath(graph, 0);
System.out.println(singleSourcePath.path(6)); // 打印从源顶点0到顶点6的路径
}
}
通过广度优先遍历算法,从源顶点s开始逐层遍历图中的顶点,通过队列的先进先出特性,保证了路径的最短性。在遍历过程中,记录每个顶点的前驱顶点,最终可以通过回溯路径找到从源顶点到目标顶点的路径。
3. 深度优先遍历与广度优先遍历对比
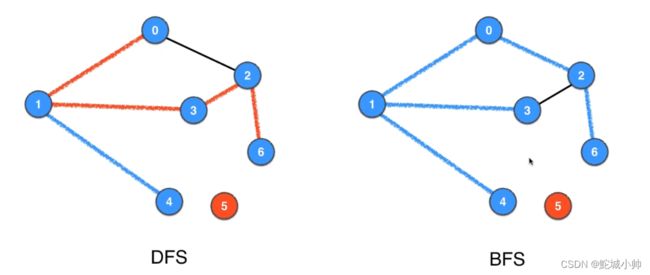
深度优先遍历:
- 从顶点0开始,递归地深度优先遍历子顶点。
- 遍历路径为0->1->3->2->6。
- 当到达顶点1时,发现顶点3已经被访问过,因此回溯到顶点1的父节点0。
- 继续遍历顶点2,然后到达顶点6。
- 最终,遍历了顶点0、1、3、2、6。
广度优先遍历:
- 从顶点0开始,通过队列进行广度优先遍历。
- 遍历路径为0->1->2->3->4->6。
- 首先遍历顶点0,然后遍历子顶点1和2。
- 在遍历顶点1时,遍历其子顶点3和4。
- 在遍历顶点2时,由于顶点3已经被访问过,因此跳过它。
- 最后,遍历顶点4和6。
- 最终,遍历了顶点0、1、2、3、4、6。
路径比较:
- 深度优先遍历的路径为0->1->3->2->6,包含了顶点0、1、3、2、6,共计5个顶点。
- 广度优先遍历的路径为0->2->6,包含了顶点0、2、6,共计3个顶点。
综上所述,广度优先遍历具有以下优势:
- 广度优先遍历是一种最短路径算法,可以找到从起始顶点到目标顶点的最短路径。
- 在示例中,广度优先遍历找到了从顶点0到顶点6的最短路径,而深度优先遍历的路径长度更长。
- 广度优先遍历通过逐层遍历子顶点,可以保证找到的路径是最短的。
4. 最短路径长度
package BFS;
/**
* @author wushaopei
* @create 2023-06-05 10:35
*/
import java.util.*;
/**
* 图的广度优先遍历(BFS)
* @author wushaopei
* @create 2023-06-05 10:04
*/
/**
* 图的单源路径问题,使用广度优先遍历(BFS)求解
*/
public class USSSPath {
private Graph G; // 图对象
private boolean[] visited; // 记录顶点是否访问过
private int s; // 源顶点
private int[] pre; // 记录顶点在路径中的前一个顶点
private int[] dis;
public USSSPath(Graph G, int s) {
this.G = G;
this.s = s;
visited = new boolean[G.V()]; // 初始化visited数组,默认所有顶点未访问
pre = new int[G.V()]; // 初始化pre数组,默认所有顶点前一个顶点为-1
dis = new int[G.V()];
for (int v = 0; v < G.V(); v++) {
pre[v] = -1;
}
bfs(s,dis); // 从源顶点s开始进行BFS遍历
}
private void bfs(int s, int[] dis) {
Queue queue = new LinkedList<>(); // 创建队列用于存储待访问顶点
queue.add(s); // 将源顶点s入队
visited[s] = true; // 标记源顶点s为已访问
dis[s] = 0;
while (!queue.isEmpty()) { // 当队列不为空时,继续遍历
int v = queue.poll(); // 出队一个顶点v
for (int w : G.adj(v)) { // 遍历顶点v的邻接顶点w
if (!visited[w]) { // 如果w未被访问过
queue.add(w); // 将w入队
visited[w] = true; // 标记w为已访问
pre[w] = v; // 设置w在路径中的前一个顶点为v
dis[w] = dis[v] + 1;
}
}
}
}
public boolean isConnectedTo(int t) {
G.validateVertex(t); // 验证目标顶点t是否合法
return visited[t]; // 返回目标顶点t是否与源顶点s相连
}
public Iterable path(int t) {
List res = new ArrayList<>();
if (!isConnectedTo(t)) return res; // 若目标顶点t与源顶点s不相连,则返回空路径
int cur = t;
while (cur != s) {
res.add(cur); // 将当前顶点加入路径中
cur = pre[cur]; // 更新当前顶点为其前一个顶点
}
res.add(s); // 将源顶点s加入路径中
Collections.reverse(res); // 反转路径列表,得到从源顶点s到目标顶点t的路径
return res; // 返回路径列表
}
public int dis(int s){
G.validateVertex(s);
return dis[s];
}
public static void main(String[] args) {
Graph graph = new Graph("g.txt");
USSSPath usssPath = new USSSPath(graph, 0);
System.out.println(usssPath.path(6)); // 打印从源顶点0到顶点6的路径
System.out.println(usssPath.dis(3)); // 打印源到顶点的路径长度
}
}
该代码实现了使用广度优先遍历求解图的单源路径问题,并提供了打印路径和计算最短距离的功能。在主方法中,通过创建图对象和USSSPath对象,可以对图进行处理并输出结果。