Matlab下实现支持向量机算法libsvm

虽然matlab中有自带的svm算法但是效果没有台湾教授的libsvm效果好。

注意：libsvm只能实现正数的预测

下面介绍一下如何在matlab上实现libsvm。

工具箱下载：GitHub - cjlin1/libsvm: LIBSVM -- A Library for Support Vector Machines

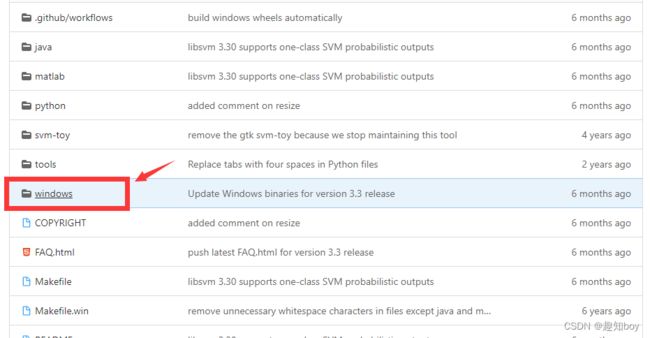
首先下载：

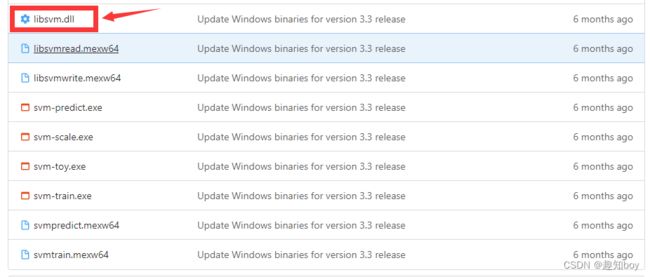
 然后点进去

 

 

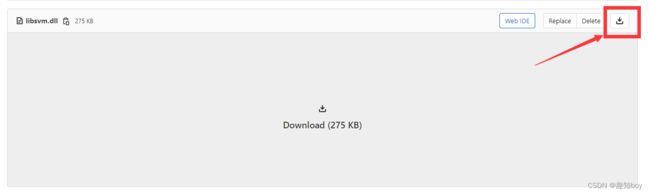
 然后保存在一个文件夹下，注意：1.windows_   要删除

2.下载下来后svmpredict.mexw64改为libsvmpredict.mexw64

svmtrain.mexw64改为libsvmtrain.mexw64

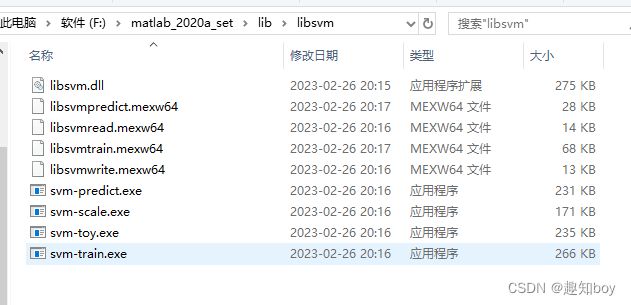
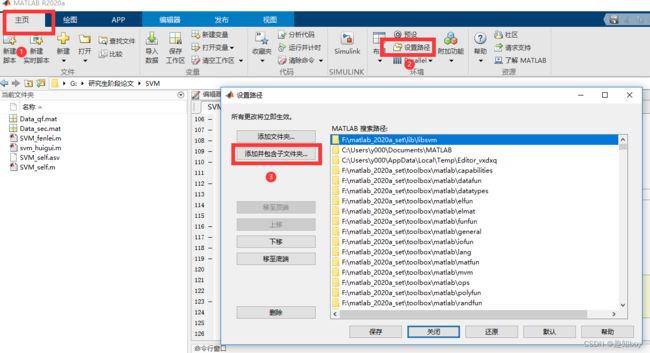
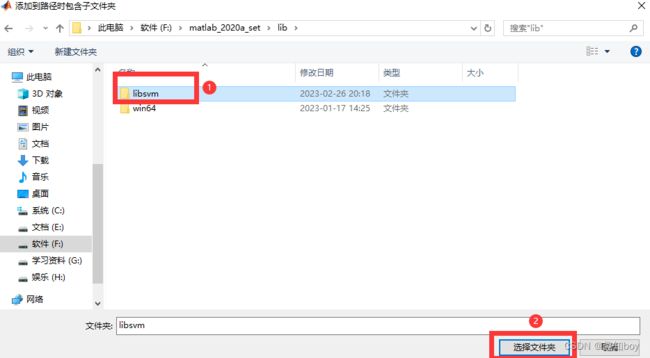
 将所有的文件放在matlab的一个安装目录下，位置都可以。

 然后在路径中添加这个文件夹的位置就可以了。

 然后给一个测试的代码

%% I. 清空环境变量
clear all
clc
%% II. 导入数据
load concrete_data.mat
 
%%
% 1. 随机产生训练集和测试集
n = randperm(size(attributes,2));
 
%%
% 2. 训练集――80个样本
p_train = attributes(:,n(1:65))';
t_train = strength(:,n(1:65))';
 
%%
% 3. 测试集――23个样本
p_test = attributes(:,n(81:end))';
t_test = strength(:,n(81:end))';
 
%% III. 数据归一化
%%
% 1. 训练集
[pn_train,inputps] = mapminmax(p_train');
pn_train = pn_train';
pn_test = mapminmax('apply',p_test',inputps);
pn_test = pn_test';
 
%%
% 2. 测试集
[tn_train,outputps] = mapminmax(t_train');
tn_train = tn_train';
tn_test = mapminmax('apply',t_test',outputps);
tn_test = tn_test';
 
%% IV. SVM模型创建/训练
%%
% 1. 寻找最佳c参数/g参数
[c,g] = meshgrid(-10:0.5:10,-10:0.5:10);
[m,n] = size(c);
cg = zeros(m,n);
eps = 10^(-4);
v = 5;
bestc = 0;
bestg = 0;
error = Inf;
for i = 1:m
    for j = 1:n
        cmd = ['-v ',num2str(v),' -t 2',' -c ',num2str(2^c(i,j)),' -g ',num2str(2^g(i,j) ),' -s 3 -p 0.1'];
        cg(i,j) = libsvmtrain(tn_train,pn_train,cmd);
        if cg(i,j) < error
            error = cg(i,j);
            bestc = 2^c(i,j);
            bestg = 2^g(i,j);
        end
        if abs(cg(i,j) - error) <= eps && bestc > 2^c(i,j)
            error = cg(i,j);
            bestc = 2^c(i,j);
            bestg = 2^g(i,j);
        end
    end
end
 
%%
% 2. 创建/训练SVM  
cmd = [' -t 2',' -c ',num2str(bestc),' -g ',num2str(bestg),' -s 3 -p 0.01'];
model = libsvmtrain(tn_train,pn_train,cmd);
 
%% V. SVM仿真预测
[Predict_1,error_1,decision_values1] = libsvmpredict(tn_train,pn_train,model); 
[Predict_2,error_2,decision_values2] = libsvmpredict(tn_test,pn_test,model);
%%
% 1. 反归一化
predict_1 = mapminmax('reverse',Predict_1,outputps);
predict_2 = mapminmax('reverse',Predict_2,outputps);
 
%%
% 2. 结果对比
result_1 = [t_train predict_1];
result_2 = [t_test predict_2];
 
%% VI. 绘图
figure(1)
plot(1:length(t_train),t_train,'r-*',1:length(t_train),predict_1,'b:o')
grid on
legend('真实值','预测值')
xlabel('样本编号')
ylabel('耐压强度')
string_1 = {'训练集预测结果对比';
           ['mse = ' num2str(error_1(2)) ' R^2 = ' num2str(error_1(3))]};
title(string_1)
figure(2)
plot(1:length(t_test),t_test,'r-*',1:length(t_test),predict_2,'b:o')
grid on
legend('真实值','预测值')
xlabel('样本编号')
ylabel('耐压强度')
string_2 = {'测试集预测结果对比';
           ['mse = ' num2str(error_2(2)) ' R^2 = ' num2str(error_2(3))]};
title(string_2)
%% VII. BP神经网络
%%
% 1. 数据转置
pn_train = pn_train';
tn_train = tn_train';
pn_test = pn_test';
tn_test = tn_test';
 
%%
% 2. 创建BP神经网络
net = newff(pn_train,tn_train,10);
 
%%
% 3. 设置训练参数
net.trainParam.epochs = 1000;
net.trainParam.goal = 1e-3;
net.trainParam.show = 10;
net.trainParam.lr = 0.1;
 
%%
% 4. 训练网络
net = train(net,pn_train,tn_train);
 
%%
% 5. 仿真测试
tn_sim = sim(net,pn_test);
 
%%
% 6. 均方误差
E = mse(tn_sim - tn_test);
 
%%
% 7. 决定系数
N = size(t_test,1);
R2=(N*sum(tn_sim.*tn_test)-sum(tn_sim)*sum(tn_test))^2/((N*sum((tn_sim).^2)-(sum(tn_sim))^2)*(N*sum((tn_test).^2)-(sum(tn_test))^2)); 
 
%%
% 8. 反归一化
t_sim = mapminmax('reverse',tn_sim,outputps);
 
%%
% 9. 绘图
figure(3)
plot(1:length(t_test),t_test,'r-*',1:length(t_test),t_sim,'b:o')
grid on
legend('真实值','预测值')
xlabel('样本编号')
ylabel('耐压强度')
string_3 = {'测试集预测结果对比(BP神经网络)';
           ['mse = ' num2str(E) ' R^2 = ' num2str(R2)]};
title(string_3)
% ————————————————
% 版权声明：本文为CSDN博主「奔跑的Yancy」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
% 原文链接：https://blog.csdn.net/lyxleft/article/details/82880860