C语言学习笔记(浙大翁恺版)第八周(数组部分)
8.1.1 初试数组
在循环中我们有一个例子:计算用户输入的整数平均数,以-1结尾。
当时的方法是:读入用户输入的每个数字,统计输入的个数,然后用输入的数字之和除以个数。
我们用累加的方法得到最后的和,不需要记录每个数字是多少。
那么问题做些更改,又该怎么做?
容易知道,我们需要记录每个数字,那么如何记录很多数?
- int num1,num2....?
我们需要一种新的手段:数组
int number[100];
scanf("%d",&number[i]);定义了一个变量叫number,这个变量是一个数组,这个数组的每个单元都是一个int,数组的大小是100(可以放100个int)
#include
int main()
{
int x;
double sum = 0;
int cnt = 0;
int number [100] ;//定义数组
scanf("%d", &x);
while(x!=-1){
number [cnt] = x;//对数组里的元素赋值
sum+=X;
cnt ++ ;
scanf("%d", &x);
}
if(cnt>0){
printf ("%f\n", sum/cnt);
int i;
for ( i=0; i sum/cnt )//使用数组元素
{
printf("%d\n",number[i]);//遍历数组
}
}
}
return 0;
}
PS:遍历就是将数组里的每个元素都过一遍或者规定的范围内过一遍
这个程序利用了数组来完成计算平均值并且输出比平均值大的数字,然而这个程序中存在安全隐患——数组的大小从一开始就固定,这个问题我们下节再说
8.1.2 数组的使用
定义数组
上一节我们定义了一个数组,它的格式是这样的:
- <类型>变量名称[元素数量]
- 如int grades[100]
- double weight [20]
- 需要注意的是:元素数量必须是整数
- C99之前元素数量必须在编译时确定,C99之后可以用变量来定义数组大小
数组的含义
- 是一种容器(放东西的东西) ,有一些特点:
- 所有的元素都是同一类型,在定义数组时就定义好了
- 一旦创建就不能改变其大小
- 在计算机内部内存中数组中的元素是按照顺序排列的
编程语言可提供容器能力的大小和语言能力大小相挂钩
如:
int a[10];a[2]=a[1]+2;- 像这样,数组单元可以出现在赋值号的左边或右边,左边称左值,右边称右值
数组的单元
在上面我们初步了解了数组单元,知道了每个单元都是和数组类型相同的变量,还有一点令人困惑,数组定义时候括号里是10,怎么数组单元的最大值变成了9呢?
我们将使用数组时放在[]中的数字叫做下标或索引,下标从0开始计数
为什么从0开始?因为C在创建之时希望将编译器尽量简化,从0开始计数可以节省资源,十分方便。在之后的语言就依此建立标准。
因此因为其广泛性,我们需要适应这个并不算合理的事情,数组单元从0开始,最大下标是数组大小减一。
下标范围
然而C语言编译器和运行环境都不会检查数组下标是否越界,所以当程序执行,对越界后的数组访问会造成许多问题,可能导致程序崩溃。当然有可能运气好,没造成严重后果,但程序可不是抽奖。
因此程序员必须保证只使用有效的下标值:[0,数组大小-1]
那么还记得上节课的例子吗?我们定义了一个大小为100的数组,但是输入的数据是有可能超过100的。所以说有安全隐患
那么如何解决?
1. 加限定条件为当输入了100个数字之后停止读入
2. C99,先输入要输入数字的个数,用此个数作为变量确定数组大小。同样的,确定之后无法更改大小。
是否能创建一个长度为0的数组?
可以,但没必要:),当定义一个长度为0的数组如a[0],其下标最大为-1,可以编译,但没有任何用处(也许可以浪费一点内存空间)
8.1.3 数组例子:统计个数
需要记录每个数字吗?当然不需要,只需要记录每个数字出现的次数。
#include
int main(void)
{
int x;
const int NUMBER = 10;//定义数组大小
int count[NUMBER];//定义数组
int i;
for(i=0;i=0&&x<=9)
{
count[x]++;//数组参与运算
}
scanf("%d",&x);
}
for(i=0;i
8.2.1 数组运算
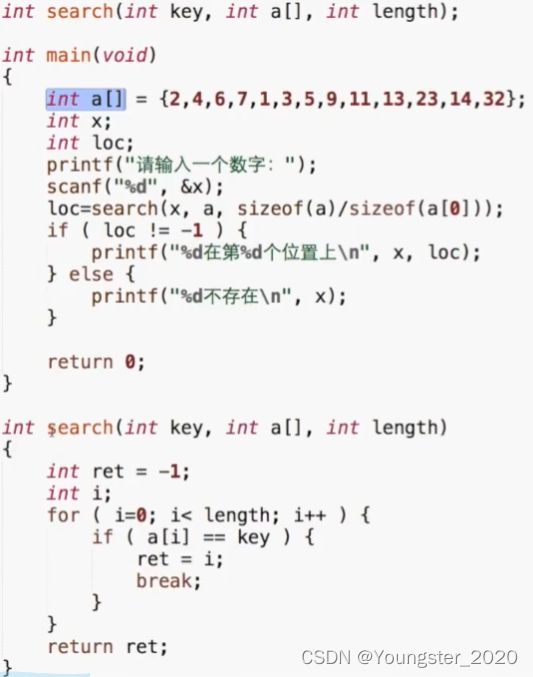
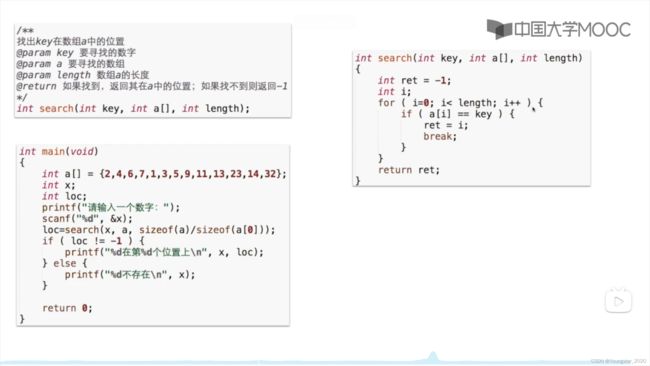
搜索,是通过用户输入的数据来确定拥有的数据中是否有相对应的。那么在一组给定的数据中,如何找出某个数据是否存在?
在这个程序中,有一条语句:
int a[] = {2,4,6,7,1,3,5,9,11,13,23,14,32};
其中没有给出数组大小,直接用大括号给出了数组的所有元素的初始值,这种定义方法不需要给出数组的大小,让编译器替你数数填入。
相反的,如果定义了数组的大小,在大括号内录入了少于数组大小-1的数据,则编译器会替你将剩余的单元填上0.
而在之前的例子中,数组初始化可以改为:
int main(void)
{
int x;
const int NUMBER = 10;//定义数组大小
int count[NUMBER]={0};//定义数组并初始化
int i;
//for(i=0;i上述代码的含义为:a[0]=2,a[2]=3,a[3]=6,其余为0.
编译器可以代替我们数出数组大小,如何得知这个值?
- sizeof:可以给出整个数组占据的内容大小,单位是字节。然后除以类型的字节单位(可以用数组单个元素大小代替),就可以得到数组大小
- sizeof(a)/sizeof(a[0])
- 这个代码的好处是当我们修改数组中初始数据时,不需要改动遍历代码
数组的赋值
int a[]={2,4,6,8,10};
int b[]=a;可以这样将数组a赋值给b数组吗?
完全不能~因为数组是特殊的变量(实际上是const)
要想将一个数组的元素赋值给另一个数组,必须采用遍历
遍历数组
通常我们使用for循环遍历数组,当设置循环变量 i>0&&i<数组长度,这样的话循环体内最大的i正好是数组最大的有效下标
常见错误:
- 循环条件错误设置为:<=数组长度
- 离开循环之后用i值做数组元素下标
search函数中,数组作为函数参数时候,因为
- 不能在[]中给出数组的大小
- 不能利用sizeof计算数组元素个数
所以需要用另一个参数来传入数组大小。而且在函数头中输入数组大小也是没有意义的
int search(int key,int a[10])
//这样的定义是没有意义的
8.2.2 数组例子:素数
我们判断素数的程序已经迭代了几次,最近的一次是用一个函数来集成功能,那这个例子和数组又有什么关系呢?
回顾一下要求:输入一个x值,判断是否为素数。函数部分用是否能找到小于自己且除了自己和1以外的值整除来判断是否是素数。
int isPrime(int x)
{
int ret=1;
int i;
if(x==1)
ret=0;
for(i=2;i这样的循环,要循环很多遍来判定是否是素数,当n很大时需要n遍,重复执行相同的代码
因此有改良版1:除2以外,偶数都不是素数,因此可以排除偶数,用从3开始的奇数判断,每次加2,将这些数进行判断,此时当样本很大时只需要循环n/2遍。
改良版2.不需要走到x-1,只需要sqrt(x)->x的平方根,此时只需要循环sqrt(x)遍。调用sqrt(x)只需要包含
改良版3.用比x小的素数来测试x是否为素数。
那么我们需要一张已有素数的表,因为素数比起全体数字来说是稀有的。如果要构造这样一张表,假如是100个素数的表,程序如下
#include
int isPrime(int x, int knownPrimes[], int numberofKnownPrimes);
int main()
{
const int NUMBER = 10;//定义数组大小10
int prime[NUMBER] = { 2 };//初始化为2,为第一个素数
int count = 1;//计数变量为1,已经有一个素数2了
int i = 3;//从3开始测试
while (count 前几种方案都是不断遍历数字,判断是否是素数。那么思考一下如果我们是直接构造一张表,最后留下来的数都是素数。算法如下:
这种方法是遍历倍数。简单来说,第一个数是2,是素数,删去2的倍数。然后下一个数字是3,是素数,删去3的倍数。下一个是5,是素数,删去5的倍数。然后是7,删去7的倍数。然后是11...依次类推,最后留在这个表里的数字就都是素数了。
伪代码如图:(n以内素数)
代码如图:
具体做法是刚开始将所有数字都赋值1,然后从2开始判断素数,将素数倍数的下标赋值0(也就意味着不是素数),并且作为筛选的条件,所以当其不作为素数时不会计数。在最后的循环会遍历输出全部素数。
PS:算法不一定和人的思考方式相同~
8.2.3 二维数组
int a[3][5] :可以理解为3行5列的矩阵。仅仅是倾向于将第一个数字作为行数,而且与线性代数中的定义合拍。
二维数组的遍历
与一维数组不同,此遍历需要用到两重循环
- a[i][j]是一个int型变量
- 表示第i行第j列
- a[i,j]什么意思?
- 逗号运算符右边的作为结果,因此相当于a[j]
二维数组的初始化
(定位就是从半中间开始定义)
二维数组例子:井字棋
#include
int main()
{
const int SIZE = 3;
int board[SIZE][SIZE];
int i,j;
int num0fX;//X
int num0f0;//O
int result = -1;//-1平局 1是X赢 0是O赢
//读入矩阵
for ( i = 0; i < SIZE; i++)
{
for ( j = 0; j < SIZE; j++)
{
scanf("%d", &board[i][j]);
}
}
//检查行
for ( i = 0; i < SIZE; i++)
{
num0f0 = num0fX = 0;
for ( j = 0; j < SIZE; j++)
{
if (board[i][j]==1)
{
num0fX++;
}
else
{
num0f0++;
}
}
if (num0f0==SIZE)
{
result = 0;
}
else if (num0fX == SIZE) {
result = 1;
}
}
//检查列
for (j = 0; j < SIZE; j++)
{
num0f0 = num0fX = 0;
for (i = 0; i < SIZE; i++)
{
if (board[i][j] == 1)
{
num0fX++;
}
else
{
num0f0++;
}
}
if (num0f0 == SIZE)
{
result = 0;
}
else if (num0fX == SIZE) {
result = 1;
}
}
//正对角线
num0f0 = num0fX = 0;
for (i = 0; i < SIZE; i++)
{
if (board[i][i] == 1)//a11 a22 a33
{
num0fX++;
}
else
{
num0f0++;
}
}
if (num0f0 == SIZE)
{
result = 0;
}
else if (num0fX == SIZE) {
result = 1;
}
}
//副对角线
num0f0 = num0fX = 0;
for (i = 0; i < SIZE; i++)
{
if (board[i][SIZE-i-1] == 1)
{
num0fX++;
}
else
{
num0f0++;
}
}
return 0;
}