算法与数据结构(四)
一、哈希表
1、哈希表在使用层面上可以理解为一种集合结构
2、如果只有key,没有伴随数据value,可以使用HashSet结构(C++中叫UnOrderedSet)
3、如果既有key,又有伴随数据value,可以使用HashMap结构(C++中叫UnOrderedMap)
4、有无伴随数据,是HashMap和HashSet唯一的区别,底层的实际结构是一回事
5、使用哈希表增(put)、删(remove)、改(put)和查(get)的操作,可以认为时间复杂度为o(1),但是常数时间比较大
6、放入哈希表的东西,如果是基础类型,内部按值传递,内存占用就是这个东西的大小
7、放入哈希表的东西,如果不是基础类型,内部按引用传递,内存占用是这个东西内存地址的大小(都是八字节)。
二、有序表
1、有序表在使用层面上可以理解为一种集合结构
2、如果只有key,没有伴随数据value,可以使用TreeSet结构(C++中叫OrderedSet)
3、如果既有key,又有伴随数据value,可以使用TreeMap结构(C++中叫OrderedMap)
4、有无伴随数据,是TreeSet和TreeMap唯一的区别,底层的实际结构是一回事
5、有序表和哈希表的区别是,有序表把key按照顺序组织起来,而哈希表完全不组织
5、红黑树、AWL树、size-balance-tree和跳表等都属于有序表结枸,只是底层具体实现不同
6、放入有序表的东西。如果是基础类型,内部按值传递。内存占用就是这个东西的大小。
7、放入有序表的东西,如果不是基础类型,必须提供比较器,内部按引用传递,内存占用是这个东西内存地址的大小。
8、不管是什么底层具体实现,只要是有序表,都有以下固定的基本功能和固定的时间复杂度。
三、链表
单链表的节点结构:
class Node {
public:
int data;
Node *next;
Node(int da = 0, Node *p = NULL) {
this->data = da;
this->next = p;
}
};
由以上结构的节点依次连接起来所形成的链叫单链表结构。
双链表的节点结构:
Class Node<V> {
v value ;
Node next;
Node last;
}
由以上结构的节点依次连接起来所形成的链叫双链表结构。
单链表和双链表结构只需要给定一个头部节点head,就可以找到剩下的所有的节点。
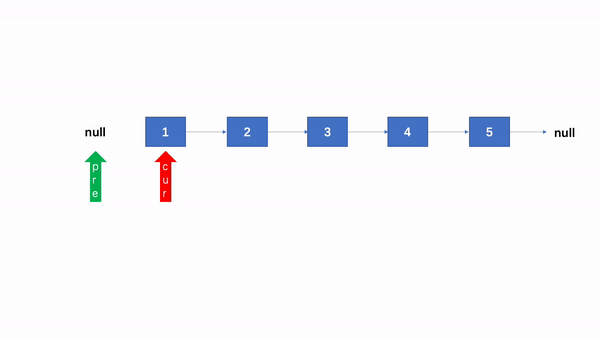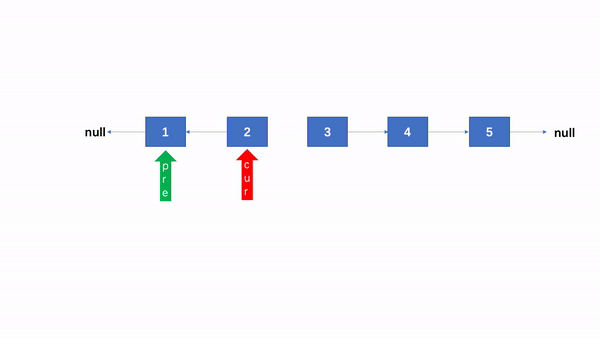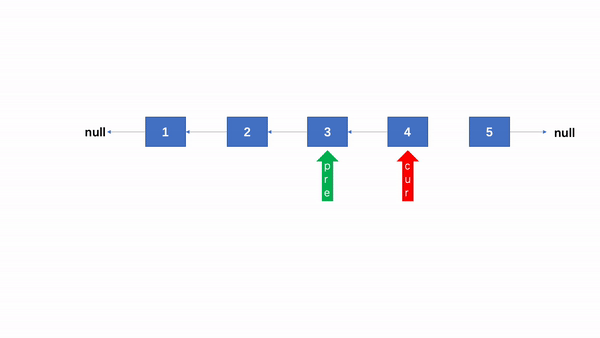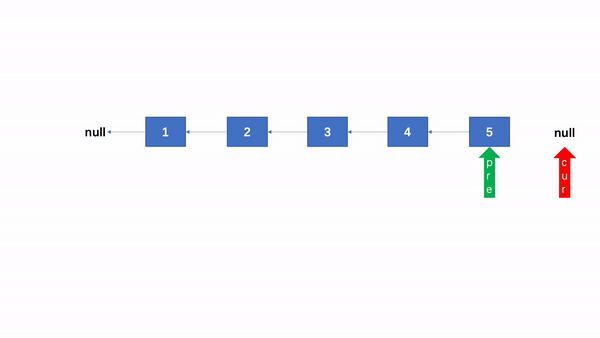
四、单链表反转
class Solution {
public ListNode reverseList(ListNode head) {
if (head == null || head.next == null) {
return head;
}
ListNode pre = null, cur = head;
while (cur != null) {
ListNode node = cur.next;
cur.next = pre;
pre = cur;
cur = node;
}
return pre;
}
}
五、面试时链表解题的方法论
1)对于笔试,不用太在乎空间复杂度,一切为了时间复杂度
2)对于面试,时间复杂度依然放在第一位,但是一定要找到空间最省的方法
重要技巧:
1)额外数据结构记录(哈希表等)
2)快慢指针
判断一个链表是否为回文结构
【题目】给定一个单链表的头节点head,请判断该链表是否为回文结构。
【例子】1->2->1,返回true;1->2->2->1,返回true;15->6->15,返回true;1->2->3,返回false。
该题如果不考虑空间复杂度的话,解决方法可以用栈的数据结构来解决如上问题,首先将链表里所有的数据全部入栈,然后再进行出站操作,如果出栈的第一个数与链表中第一个数相同,则继续出栈,如果有中途有一个数据没有对上,则非回文,如果所有数据均出栈晚上,且所有数据都一致,则为回文。
我们也可以只将链表的后半部分入栈,然后再挨个出栈与链表的第一个数及其后面的数据进行对比,规则同上。
但是链表是一个未知长度的数据结构,我们怎么才能知道链表的中间值呢,这时候我们就需要快慢指针的操作,也就是快指针每次走两个节点,慢指针一次走一个节点,当快指针到达链表的结尾时,慢指针也就指向了链表的终点。
代码如下:
#include【例子】如果链表长度为N,时间复杂度达到O(N),额外空间复杂度达到O(1)。
但如果限制额外空间复杂度达到O(1)时,我们就可以利用快慢指针的操作了,当慢指针找到了终点时,需要将慢指针之后的链表进行反转,反转完成后再设置两个指针,一个指针从链表开始与一个指针从链表结尾开始,一一进行对比,对比机制同上,当返回true或者fales之后我们再将后半部分的链表恢复到之前的状态,完成操作。
// 链表长这样
struct ListNode {
int val;
ListNode *next;
ListNode() : val(0), next(nullptr) {}
ListNode(int x) : val(x), next(nullptr) {}
ListNode(int x, ListNode *next) : val(x), next(next) {}
};
class Solution {
public:
bool isPalindrome(ListNode* head) {
//如果传进来的是空指针或者只有一个值 直接返回true
if(head->next == nullptr||head == nullptr)
return true;
//定义快慢指针
struct ListNode *slow = head;
struct ListNode *fast = head;
//通过快慢指针找出右半边链表的头
while(fast->next != nullptr && fast->next->next != nullptr){
slow = slow->next;
fast = fast->next->next;
}
fast = slow->next; //此时fast为右半链表的头地址
slow->next = NULL; //在左边结束的节点之后设置一个空值
//下面是实现右半链表的反转
struct ListNode *store = NULL;
while(fast != nullptr){
//记录左边第一个节点的地址
store = fast->next;
//将右边头结点的指针域指向左边的尾部
fast->next = slow;
//两个辅助指针右移
slow = fast;
fast= store;
}
//右边最后一个节点的指针
store = slow;
//记录左边第一个指针
fast = head.next;
bool res = true;
//最终就是从头到尾开始比较各结点的值 如果出现不相等的则return false
while(slow != nullptr && fast != nullptr){
if(slow->val != fast->val)
{
res = false;
break;
}
//两个指针同时移动
rhead = slow->next;
fast = fast->next;
}
//将右半部分的链表再逆序回去
//记录右边第一个节点的地址
slow = store.next;
store.next = NULL;
while(slow != NULL)
{
fast = slow.next;
slow.next = store;
store = slow;
slow = fast;
}
return res;
}
};
六、将单向链表按某值划分成左边小、中间相等、右边大的形式
【题目】给定一个单链表的头节点head,节点的值类型是整型,再给定一个整数pivot。实现一个调整链表的函数,将链表调整为左部分都是值小于pivot的节点,中间部分都是值等于pivot的节点,右部分都是值大于pivot的节点。
【进阶】在实现原问题功能的基础上增加如下的要求
【要求】调整后所有小于pivot的节点之间的相对顺序和调整前一样
【要求】调整后所有等于pivot的节点之间的相对顺序和调整前一样
【要求】调整后所有大于pivot的节点之间的相对顺序和调整前一样
【要求】时间复杂度请达到O(N),额外空间复杂度请达到O(1)。
//将链表分成三个部分:
//分别为小于p、等于p、大于p
//分别用一串链表连接起来,最终,连接成一个链表
ListNode* listPartition2(ListNode* head, int num) {
ListNode* sH = NULL;
ListNode* sT = NULL;
ListNode* eH = NULL;
ListNode* eT = NULL;
ListNode* bH = NULL;
ListNode* bT = NULL;
ListNode* next = NULL;
while (head != NULL) {
next = head->next;
head->next = NULL;
if (head->val < num) {
if (sH == NULL) {
sT = head;
sH = head;
}
else {
sT->next = head;
sT = head;
}
}
else if (head->val > num) {
if (bH == NULL) {
bH = head;
bT = head;
}
else {
bT->next = head;
bT = head;
}
}
else{
if (eH == NULL) {
eH = head;
eT = head;
}
else {
eT->next = head;
eT = head;
}
}
head = next;
}
if (sT != NULL) {
sT->next = eH;
eT = eT == NULL ? sT : eT;
}
if (eT != NULL) {
eT->next = bH;
}
return sH != NULL ? sH : (eH != NULL ? eH : bH);
}
七、复制含有随机指针节点的链表
【题目】一种特殊的单链表节点类描述如下
class Node
{
int value;
Node next;
Node rand;
Node(int val){
value = val;
}
}
rand指针是单链表节点结构中新增的指针,rand可能指向链表中的任意一个节点,也可能指向null。给定一个由Node节点类型组成的无环单链表的头节点head,请实现一个函数完成这个链表的复制,并返回复制的新链表的头节点。
【要求】时间复杂度0(N),额外空间复杂度0(1)
ListNode* copyListWithRand(ListNode* head) {
if (head == NULL) {
return NULL;
}
ListNode* cur = head;
1->1'->2
while (cur != NULL) {
//克隆出一个新的节点
ListNode* node = new ListNode(cur->val);
//将当前节点的指针指向赋值给克隆出新节点的指向
node->next = cur->next;
//将当前节点指向新的节点
cur->next = node;
//向下移动
cur = node->next;
}
cur = head;
while (cur != NULL) {
//找到克隆节点
ListNode* node = cur->next;
//将原节点的rand赋给克隆节点的rand
node->random = cur->random == NULL ? NULL : cur->random->next;
//指针向下移动
cur = node->next;
}
//开始分离原结点和克隆节点
cur = head;
//设置克隆节点的头
ListNode* cloneHead = head->next;
while (cur->next != NULL){ //注意边界处理,不然容易溢出
//克隆结点
ListNode* node = cur->next;
//将克隆结点的指针指向赋值给原结点的指针域
cur->next = node->next;
//指针移动
cur = node;
}
return cloneHead;
}
八、两个单链表相交的一系列问题
单链表可能有环,也可能无环。给定两个单链表的头节点 head1和head2,这两个链表可能相交,也可能不相交。请实现一个函数, 如果两个链表相交,请返回相交的第一个节点;如果不相交,返回null 即可。
【要求】如果两个链表长度之和为N,时间复杂度请达到0(N),额外空间复杂度请达到O(1)。
思路:
1、首先判断两个链表是不是有环,采用快慢指针的方法,慢指针从链表第二个元素开始出发,快指针从链表第三个元素开始出发。如果链表有环,则两个指针必定会在环内相遇,如果快指针首先到达了NULL,则无环。然后快指针返回到链表的初始结点,慢指针不动,两个指针同时开始移动一个元素。则两个指针会在入环结点相遇。
2、判断完有环无环后则需要分情况进行讨论了。
**首先是两个链表都无环:**记录两个链表的长度,并且判断两个链表的最后一个结点的地是否一致,如果一致,则一定相交。然后长链表指针的初始值设定在两个链表长度插值处,短链表指针从头开始,两个指针相遇的第一个结点则是相交的第一个结点。
**两个都有环:**首先判断两个链表的入环结点是否一致,如果一致,返回到上一个两个都无环的链表相交问题,唯一的区别就是这两种情况在计数时的终止结点不一致,上面那种是两个指针都指向NULL结束,而此种情况是到第一个入环结点结束。而下图的一、三的情况判断是一致的,如果两个入环结点不一致,则使用其中的一个入环结点继续往下走,如果在走的过程中与另外一个入环结点相等,则为三情况,否则为1情况。如果为情况一,则没有相交结点,如果为情况三,两个入环结点的第一个相交点为两个其中任意一个都可以。
**一个有环一个无环的情况:**这种情况并不会相交。
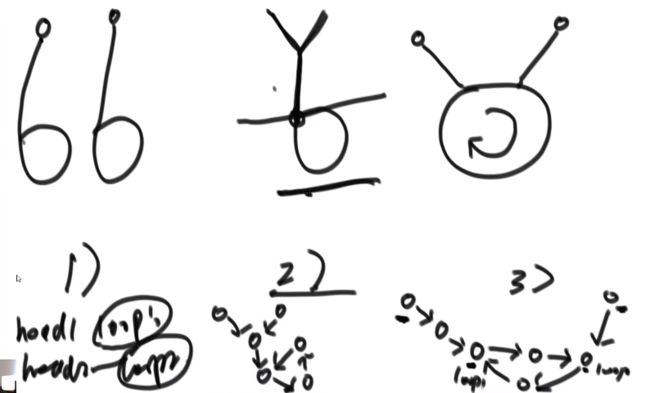
/*
这个问题要考虑几种情况:
1. 两个链表都是单链表,判断入环节点
2. 两个链表都有环,判断入环节点
3. 一个链表有环,一个链表无环,则一定不想交。因为它们都是单链表。
*/
ListNode* findFirst(ListNode* head1, ListNode* head2){
//判断两个结点是否有环
ListNode* loop1 = isLoop(head1);
ListNode* loop2 = isLoop(head2);
//如果都无环
ListNode* firstNode = NULL;
if (loop1 == NULL && loop2 == NULL) {
firstNode = noLoop(head1, head2);
}
//如果都有环
else if (loop1 != NULL && loop2 != NULL) {
firstNode = bothLoop(head1, head2, loop1, loop2);
}
//如果一个有环一个无环
else {
firstNode = NULL;
}
return firstNode;
}
//判断一个链表是否有环
//返回入环的节点
ListNode* isLoop(ListNode* head) {
if (head == NULL || head->next == NULL || head->next->next == NULL) {
return NULL;
}
//设置快慢指针的初始位置
ListNode* slow = head->next;
ListNode* fast = head->next->next;
//如果快指针或者慢指针到了NULL,则返回
while (slow != fast) {
if (fast->next == NULL || fast->next->next == NULL) {
return NULL;
}
slow = slow->next;
fast = fast->next->next;
}
//将快指针设置为头结点
fast = head;
//两个指针开始同时只移动一步
while (slow != fast) {
slow = slow->next;
fast = fast->next;
}
//返回遇到的第一个结点
return slow;
}
//都无环的情况
ListNode* noLoop(ListNode* head1, ListNode* head2) {
if (head1 == NULL || head2 == NULL) {
return NULL;
}
//设置暂存链表长度的变量n
int n = 0;
ListNode* cur1 = head1;
ListNode* cur2 = head2;
//记录第一个链表的长度
while (cur1->next != NULL) {
n++;
cur1 = cur1->next;
}
//记录第二个链表与第一个链表的插值
while (cur2->next != NULL){
n--;
cur2 = cur2->next;
}
//如果两个链表最后一个结点不相等,则不相交
if (cur1 != cur2) {
return NULL;
}
//如果第一个链表长,则将第一个头结点赋值给变量cur1,否则将第二个头结点赋值给变量cur1
cur1 = n > 0 ? head1 : head2;
//将其余一个链表的头节点赋值给变量cur2
cur2 = cur1 == head1 ? head2 : head1;
//对n进行取绝对值操作
n = abs(n);
//将较长链表的指针设定在两个链表长度差大小的结点处
while (n != 0) {
n--;
cur1 = cur1->next;
}
//两个指针同时移动
while (cur1 != cur2) {
cur1 = cur1->next;
cur2 = cur2->next;
}
//返回第一个相交的结点
return cur1;
}
//都有环的情况
ListNode* bothLoop(ListNode* head1, ListNode* head2, ListNode* loop1, ListNode* loop2) {
ListNode* cur1 = NULL;
ListNode* cur2 = NULL;
//首先如果符合上图中的情况二
if (loop1 == loop2) {
int n = 0;
cur1 = head1;
cur2 = head2;
//记录链表一的长度
while (cur1 != loop1) {
n++;
cur1 = cur1->next;
}
//记录链表一与链表二的长度
while (cur2 != loop2) {
n--;
cur2 = cur2->next;
}
//与上一个情况一致
cur1 = n > 0 ? head1 : head2;
cur2 = cur1 == head1 ? head2 : head1;
n = abs(n);
while (n != 0){
n--;
cur1 = cur1->next;
}
while (cur1 != cur2){
cur1 = cur1->next;
cur2 = cur2->next;
}
return cur1;
}
//判断情况一三
else {
cur1 = loop1->next;
//判断是否符合情况三
while (cur1 != loop1){
if (cur1 == loop2) {
return loop1;
}
cur1 = cur1->next;
}
return NULL;
}
}