原地顺时针旋转矩阵(leetcode 48.选择图像)
本题目在leetcode上有原题48. 旋转图像
详细讲解
顺时针旋转90°,横变竖,竖变横。按圈分解,一圈圈的单独转,由外圈到内圈,不断分解。
每一圈转到位了,整个矩阵就旋转好了。
那么,问题来了,如何实现原地旋转一个圈 ?
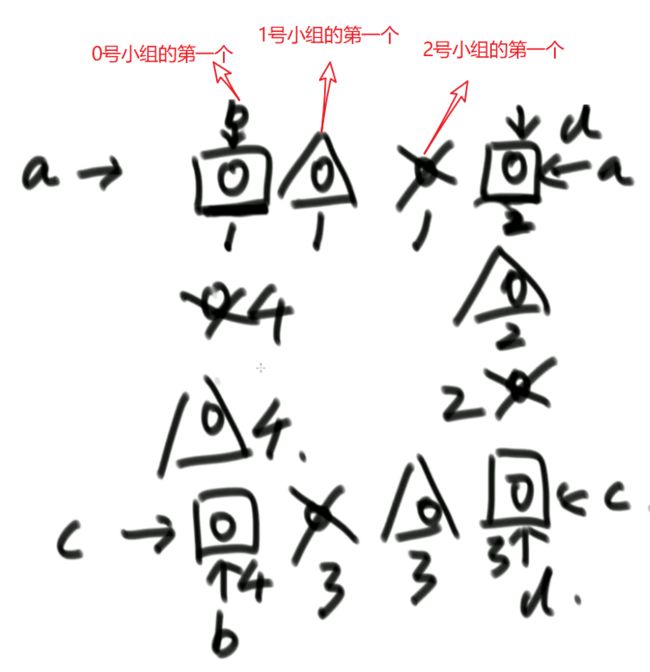
还是分解,我们把矩阵的一圈分解成多个部分,如下图所示:
你发现了吗,口、△、X,口、△、X,口、△、X,口、△、X,顺时针循环的。
外圈是4*4 ,分成3个组,lowR - topR = 3
所以,小组数 = lowR - topR (或lowC-topC)
topR,topC就是左上角,对应图中的a,b
lowR,lowC就是右下角,对应图中的c,d
不管一共分成了几个组,每个组自己旋转交换位置时 只用了4个位置,因为只有4个边
下面这句话很重要:
所以,每个小组的第一个位置是:matrix[topR][topC+i] // i为小组号. 行固定,都在这个行上
topR,topC就是左上角,对应图中的a,b
lowR,lowC就是右下角,对应图中的c,d下面这句话很重要:
所以,每个小组的第二个点(位置)是:matrix[topR+i][lowC] //i为小组号。 列固定,都在这个列上
同理,
每个小组的第三个点(位置)是:matrix[lowR][lowC-i]
每个小组的第四个点(位置)是:matrix[lowR-i][topC]
每个小组只需要用4个位置,就能旋转好,因为只有4条边。
//旋转矩阵
public class Code06_RotateMatrix {
public static void rotate(int[][] matrix) {
//左上角和右下角
int topR = 0;
int topC = 0;
int lowR = matrix.length - 1;
int lowC = matrix[0].length - 1;
//往中间内聚,即左上角往右下方移动;右下角往左上方移动。其实就是不断换圈,指定圈的左上角和右下角即可
//因为 左上角和右下角可以确定一个矩阵圈
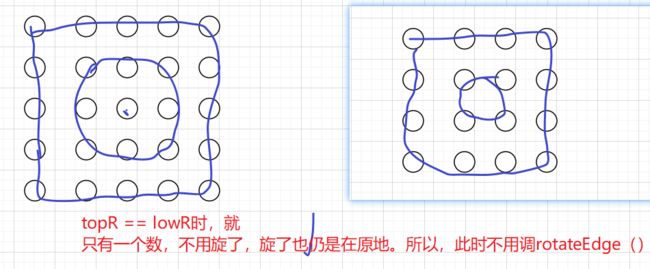
while (topR != lowR+1) {//因为是方阵。所以行不越界就够了。等效于topR < lowR
rotateEdge(matrix, topR++, topC++, lowR--, lowC--);
}
}
//旋转一个圈。只用有限几个变量,不用额外空间,空间复杂度O(1)
//topR,topC 左上角
//lowR,lowC 右下角
public static void rotateEdge(int[][] m, int topR, int topC, int lowR, int lowC) {
int tmp = 0;
//一个圈被分成了不同的组,一圈共有lowC-topC个组(或写成lowR - topR). 只要每个组能旋转正确,整个圈就能旋转正确。
for (int i = 0; i < lowR - topR; i++) {//i代表组号。从0开始
//写代码的时候,并不是按照1->2,2->3。。的顺序.不要简单死背套用两数交换的代码,是错的。要理解实质才会写对
tmp = m[topR][topC + i];//m[topR][topC + i]是当前组的第1个。每个组第1个都在第一行,即与左上角同行。
//因为1位置的数备份了,相当于腾出了一个位置1,所以,让4过来
m[topR][topC + i] = m[lowR-i][topC];//m[lowR-i][topC]当前组的第4个
//因为4已经转移到1了,已经弄好了,所以让3过来
m[lowR-i][topC] = m[lowR][lowC-i];//m[lowR][lowC-i] 当前组的第3个
//3弄好了,让2过来
m[lowR][lowC-i] = m[topR+i][lowC];//m[topR+i][lowC]当前组的第2个
//2弄好了,从备份里把1拿出来,让1过去
m[topR+i][lowC] = tmp;
}
}
public static void printMatrix(int[][] matrix) {
for (int i = 0; i != matrix.length; i++) {
for (int j = 0; j != matrix[0].length; j++) {
System.out.print(matrix[i][j] + " ");
}
System.out.println();
}
}
public static void main(String[] args) {
int[][] matrix = { { 1, 2, 3, 4 }, { 5, 6, 7, 8 }, { 9, 10, 11, 12 }, { 13, 14, 15, 16 } };
printMatrix(matrix);
rotate(matrix);
System.out.println("=========");
printMatrix(matrix);
/* 1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
=========
13 9 5 1
14 10 6 2
15 11 7 3
16 12 8 4*/
}
}
简洁注释版
在leetcode上直接通过,100%
class Solution {
public void rotate(int[][] matrix) {
// 左上角、右下角
int topR = 0;
int topC = 0;
int lowR = matrix.length -1;
int lowC = matrix[0].length -1;
while(topR < lowR){
rotateEdge(matrix,topR++,topC++,lowR--,lowC--);
}
}
public void rotateEdge(int[][] m,int topR,int topC,int lowR,int lowC){
for(int i = 0 ; i < lowC - topC;i++){
//每组的1号暂存. 腾出位置了,让需要过来的过来即可
int temp = m[topR][topC+i];
//4-->1 。 m[lowR-i][topC]就是每组的4号
m[topR][topC+i] = m[lowR-i][topC];
//3-->4
m[lowR-i][topC] = m[lowR][lowC-i];
//2-->3
m[lowR][lowC-i] = m[topR+i][lowC];
//从缓存里拿出1,放到2,1-->2
m[topR+i][lowC] = temp;
}
}
}