2023年度第四届全国大学生算法设计与编程挑战赛(春季赛)
目录
- 2023年度第四届全国大学生算法设计与编程挑战赛(春季赛)
-
- 1、A
- 2、Bx
- 3、Cut
- 4、Diff
- 5、EchoN
- 6、Farmer
- 7、GcdGame
- 8、HouseSub
- 9、IMissYou!
- 10、Jargonless
2023年度第四届全国大学生算法设计与编程挑战赛(春季赛)
1、A
题目描述
有一个长为n(1≤n≤1000) 的序列,序列上的元素两两不同。你需要用最少的操作步数翻转这个序列。
每次操作你需要给出三个数 i,j,k(1≤i≤j<k≤n),交换序列中下标属于 [[i,j] 的元素与下标属于[j+1,k] 的元素。例如:对于长为 7 的序列 1,2,3,4,5,6,7,进行操作i=2,j=4,k=6 后序列会变为 1,5,6,2,3,4,7。
给定 n,你需要输出最少的操作步数,并输出每一步的具体操作。保证对于所有输入的 n,均存在至少一个有限步内的合法操作。
输入
一行,一个整数 n。
3
输出
2
1 1 3
1 1 2
第一行一个非负整数 m,表示最少的操作步数。
接下来 m 行,每行三个整数 i,j,k,表示进行题目中描述的操作。
要求 1≤i,j,k≤n,i≤j<k。
你的输出必须保证从上到下执行这 m* 次操作后,整个序列被翻转。
代码
#todo
2、Bx
题目描述
你有一个长度为 n (2≤n≤106) 的 01 序列,你可以执行如下操作若干遍:
每次操作可以选择一个正整数 i,满足 1≤i≤n−k+1,然后选中[i,i+k−1] 这个长度为k (2≤k≤n) 的区间,设这个区间当前的数的最大值为 x*,然后将这个区间中所有的数变成 x。
一个操作序列 i1,i2,⋯,im 是好的当且仅当依次进行这些操作后,整个序列的数都变成 1。
你需要给出一个好的操作序列,使得这个操作序列的长度最小,且满足此情况下,操作序列的字典序最小。
输入
第一行一个整数 T(1≤T≤105),表示数据组数。
对于每组数据:第一行两个整数n,k。
第二行一个长度为 n 的01字符串,表示这个序列。数据保证序列中至少有一个 1和一个 0。
数据保证 ∑n≤106。
2
5 3
00010
6 4
100001
输出
2
3 1
2
1 2
对于每组数据,输出两行:第一行一个整数 m,表示最短的操作次数。
第二行 m 个整数,表示这个操作序列,中间用空格分隔开。
代码
#todo
3、Cut
题目描述
我们可以对数字进行一些有趣的游戏,比如,把数字全部切开又能变成多少?
你现在随意地写下了一个数字n (1≤n<1010),你现在可以任意多次从任意位置切开这个数字,随后将切开的数字加起来,得到一个结果。
你现在想知道所有可能的切法结果的和是多少。
输入
输入一行一个整数 n,表示一开始写下的数字。
125
输出
176
对于样例给出的数字 125,有以下几种切法的可能:
- 125
- 1+25=26
- 12+5=17
- 1+2+5=8
故算式结果的和为 125+26+17+8=176。
代码
s = input()
li = []
lis = []
#简单的回溯
def dfs(s):
if len(s) < 1:
lis.append(li.copy())
return
if len(s) == 1:
li.append(s)
lis.append(li.copy())
li.pop()
return
for i in range(1, len(s)+1):
li.append(s[0:i])
dfs(s[i:len(s)])
li.pop()
dfs(s)
res = 0
for i in lis:
for j in i:
res += int(j)
print(res)
4、Diff
题目描述
作为一个居家小能手,你深知收纳之道。
至少,同一种东西不要放在一起,因为同样的东西放在一起容易分不出来……。
现在有n (1≤n≤1000) 个盒子,你现在有 k (2≤k≤1000) 种物品,每种物品的数量有无限个。你现在要在每个盒子里都放一个物品,同时,你不想相邻的位置上摆同样的东西。
想请问有多少种摆放方式可以满足你的要求。
输入
输入一行两个整数 n、k,表示盒子的数量和物品种类的数量。
3 2
输出
2
输出一行一个整数,表示方案数,数据保证答案在 int 范围内。
代码
n, m = map(int, input().split())
#简单的数学问题
res = 1
res *= m
for i in range(n-1):
res *= (m-1)
print(res)
5、EchoN
题目描述
人类的本质是复读机,就是说,人类,人类的本质,是一些东西……人类的本质是什么?人类的本质是复读,人类的本质是复读机。
给定一个字符串 S (∣S∣⩽106),如果其中某一个子串是 S 的前缀,那么我们就说存在一次复读。
想请问一共有多少次复读。
输入
一行一个字符串 S。
aaba
输出
6
一行一个整数,表示复读次数。
代码
s = input()
res = len(s)
for i in range(1, len(s)):
start = 0
while i<=len(s)-1 and s[i] == s[start]:
res += 1
i += 1
start += 1
print(res)
6、Farmer
题目描述
不同的人对于不同的教育方法的接受程度是不一样的,不同的树对于不同的肥料的吸收程度也是不一样的。路边现在种着一排的树,作为新时代新青年的你当然有义务来做些什么,你的手里提着各式各样的化肥。“怎么样才能够成为一个优秀的农民呢?”年纪轻轻的你已经立下了成为农民的远大志向。“这些树,要好好施肥才能茁壮成长啊。”
路边有 n (2⩽n⩽5×103) 棵树,编号从 1 到 n,其中第 i 棵树和第 i+1 棵树之间的距离是 Ai (1⩽Ai⩽109)。现在手上有 m (1⩽m⩽200) 袋肥料,对第 i棵树使用第 j 袋肥料可以获得 Bi,j(1⩽ Bi,j⩽109) 的收益。每一袋肥料只能用在一棵树上,但是一棵树可以用很多袋肥料。
现在定义满意度为得到的收益减去走过的距离,即 ∑B−∑A,如果你可以从任何一棵树开始走,请问你能得到的最大满意度为多少?
需要注意:
1. 你可以按照任意顺序使用化肥,可以先某棵树使用第1、3、5袋化肥,再前往另一棵树使用第2、4袋化肥
2. 你可以在树与树之间任意走动,即可任意往返
输入
第一行两个整数 n、m,表示树的数量和肥料的数量。
接下来一行n−1 个整数 A1,A2,…An−1,表示树之间的距离。
接下来 n行,每行 m 个整数Bij,表示每袋肥料的收益。
3 4
1 4
2 2 5 1
1 3 3 2
2 2 5 1
输出
11
输出一行一个整数,表示最大满意度。
代码
#todo
7、GcdGame
题目描述
有一个长为n (1≤n≤105)的正整数序列,第i个数为ai (2≤ai≤108)。你在这个序列上进行q (1≤q≤105)轮单人游戏,每轮游戏之间相互独立。
在一轮游戏中,你有两个棋子,初始放在序列的第x个位置和第y个位置(1≤x,y≤n);棋子有权值,初始分别为ax和ay。你的目标是让这两个棋子上的权值不互质。每一步,你可以选择一枚棋子,将其移动到序列上相邻的一个位置,即从第i个位置移动到第i−1或第i+1个位置,同时这个棋子上的权值会乘上ai−1或ai+1。注意,第1个位置只能移动到第2个位置,第n个位置只能移动到第n−1个位置。
对于这q轮游戏,请输出每轮游戏达成目标的最小操作步数。
输入
第一行,两个正整数n,q,分别表示序列长度和询问次数。
第二行,n个正整数,第i个数表示ai的值。
接下来q行,每行两个正整数x,y,表示一轮游戏的初始状态。
6 4
2 9 5 7 4 3
4 1
2 6
3 4
5 2
输出
1
0
1
1
q行,每行一个整数,第i行的整数表示第i次询问的答案。
代码
#todo
8、HouseSub
题目描述
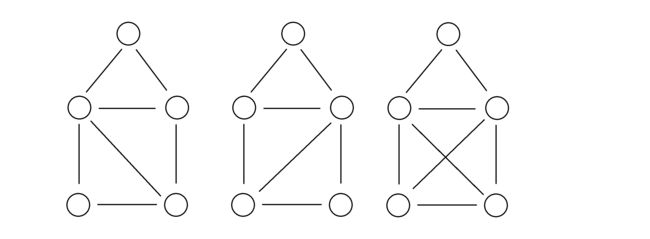
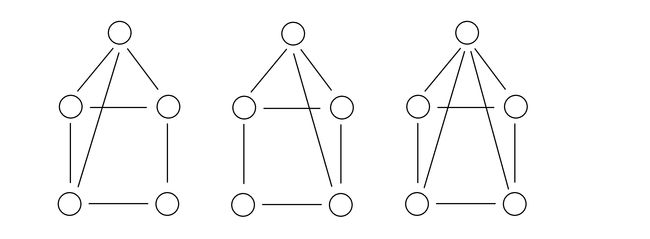
一个图称之为“房子”当且仅当这个图是这样的:
有一个 n (5≤n≤105) 个点 m (5≤m≤105) 条边的无向图,小L想找到 5 个不同的点,并满足这 5 个点能构成一个房子。但对于这 5 个点,下方的四元环必须是“纯四元环”。也就是说,不能出现以下几种情况:
需要注意的是,以下情况是合法的,因为下方的四元环不相邻的两个点对间没有边相连:
具体地,设这 5 个互不相同的点为u1,u2,u3,u4,u5,小L 想找到满足 u1<u2 且(u1,u2),(u1,u3),(u2,u3),(u1,u4),(u4,u5),(u5,u2) 间有边相连,但 (u1,u5) 和(u2,u4) 间不存在边相连的,(u1,u2,u3,u4,u5) 五元组的方案数。
输入
第一行一个整数 T,表示数据组数。
对于每组数据:第一行两个整数n,m ,表示无向图的点数和边数。
第2∼(m+1) 行,每行两个整数 x,y(1≤x,y≤n,x!=y),表示无向图中的一条边。
保证无向图不存在重边或自环。保证 1≤∑n,∑m≤105。
5 6
1 2
1 3
2 3
1 4
4 5
2 5
输出
1
一行一个整数,表示方案数对 998244353998244353 取模后的结果。
代码
#todo
9、IMissYou!
题目描述
作为一个离家千里的大学生,夜深时你总会思念你的家人。
为了科学研究深夜思念的规律,你记录了这一周内每天的思念值ai (∣ai∣≤100),你想知道这一周内你有多思念家人。如果你的思念值之和严格大于0,则代表思念家人,反之则不思念。
在思念时请输出’IMissYou!‘,并给出总思念值,反之则单独输出’OvO’。(输出时均不包含单引号)。
输入
第一行七个正整数 ai,意义如上所述。
5 5 5 5 5 -2 -2
输出
IMissYou!
21
一行或两行,表示答案。
代码
li = input().split()
sum1 = 0
for i in li:
sum1 += int(i)
if sum1 > 0:
print('IMissYou!')
print(sum1)
else:
print('OvO')
10、Jargonless
题目描述
很多人一些话翻来覆去说得没有任何营养,有用信息就一点点……如果可以不用废话文学,请不要使用废话文学。
给定一个原始文本字符串 S (∣S∣≤3×105) 和一个有用信息字符串 T (∣T∣≤200),现在可以对 S 进行精简操作,具体来说,就是可以将 S 的开头和结尾分别去掉一段,使得剩下的字符串 ′S′ 中包含有有用信息 T*。
请问有多少种精简 S 的方式?
注意:′S′包含T指的是T*是′S′的子序列,如’aacbac’包含’abc’。
输入
第一行一个字符串 S*,表示原始的文本。
第二行一个字符串 T*,表示有用的信息。
abcabcabc
cba
输出
9
输出一行一个整数,表示精简 S 的方案数。
代码
s = input()
t = input()
def conTains(s, t):
index1 = 0
for i in s:
if index1 <len(t) and t[index1] == i:
index1 += 1
if index1 == len(t):
return True
else:
return False
res = 0
l = 0
r = 0
while conTains(s[l:], t):
r = 1
res += 1
while conTains(s[l:len(s) - r], t):
# print(f'left:{l}, right:{r}')
res += 1
r += 1
l += 1
print(res)