机器学习的一些常见算法介绍【线性回归，岭回归，套索回归，弹性网络】

系列优秀文章目录

在vmbox里面安装Ubuntu16.04并且配置jdk以及Hadoop配置的教程【附带操作步骤】_张小鱼༒的博客-CSDN博客

centos7配置静态网络常见问题归纳_张小鱼༒的博客-CSDN博客

jupyter notebook第八章pyecharts库的一些案例分析加相关函数的解析_jupyter安装pyecharts_张小鱼༒的博客-CSDN博客

python当中的第三方wxPython库的安装解答_pip install wx_张小鱼༒的博客-CSDN博客

文章目录

目录

系列优秀文章目录

前言

一、机器学习概述

1.1、概述

1.2、理性认识

1.3、机器学习、数据分析、数据挖掘区别与联系

二、一些案例介绍

1.基于一元线性回归公式和向量形式计算线性权重和偏置值

2.梯度下降法的使用

3、批量梯度下降法

4、多项式线性回归

 5、使用四种线性回归对波斯顿房价进行分析

总结

---

前言

本篇主要介绍机器学习的一些算法，例如一元线性回归，岭回归，套索回归，弹性网络回归，逻辑斯蒂回归，knn算法等等

---

提示：以下是本篇文章正文内容，下面案例可供参考

一、机器学习概述

1.1、概述

1. 机器学习是一门从数据中研究算法的科学学科。
2. 机器学习直白来讲，是根据已有的数据，进行算法选择，并基于算法和数据构建模型，最终对未来进行预测。
3. 通过数据训练出一个模型->预测未知属性。

1.2、理性认识

输入： x ∈ X（属性值）
输出： y ∈ Y(目标值 )
获得一个目标函数(target function):
f : X ∈ Y(理想的公式)
输入数据:D = {(x1,y1),(x2,y2),…,(xn,yn)}(历史信息)
最终具有最优性能的假设公式：
g : X → Y(学习得到的最终公式 )
{(Xn,Yn)} from f → ML → g
目标函数f未知（无法得到）
假设函数g类似函数f，但是可能和函数f不同
机器学习中是无法找到一个完美的函数f
机器学习
从数据中获得一个假设的函数g，使其非常接近目标函数f的效果
概念
拟合：构建的算法符合给定数据的特征
x(i) :表示第i个样本的x向量
xi: x向量的第i维度的值

1. 鲁棒性：也就是健壮性、稳健性、强健性,是系统的健壮性；当存在异常数据的时候，算法也会拟合数据过拟合和欠拟合显示
2. 过拟合：算法太符合样本数据的特征，对于实际生产中的数据特征无法拟合–模型在这个数据集展示的特别好
3. 欠拟合：算法不太符合样本的数据特征–训练集不好（不存在函数或者假设不对）

1.3、机器学习、数据分析、数据挖掘区别与联系

• 数据分析：数据分析是指用适当的统计分析方法对收集的大量数据进行分析，并提取有用的信息，以及形成结论，从而对据进行详细的研究和概括过程。在实际工作中，数据分析可帮助人们做出判断；数据分析一般而言可以分为统计分析、探索性数据分析和验证性数据分析三大类。
• 数据挖掘：一般指从大量的数据中通过算法搜索隐藏于其中的信息的过程。通常通过统计、检索、机器学习、模式匹配等诸多方法来实现这个过程。
• 机器学习：是数据分析和数据挖掘的一种比较常用、比较好的手段
   

二、一些案例介绍

1.基于一元线性回归公式和向量形式计算线性权重和偏置值

代码如下（示例）：

#定义numpy数组数据，分别基于一元线性回归公式和向量形式计算线性权重和偏置值；
#计算结果与ScikitLearn中提供的线性回归函数计算结果进行比较。
import numpy as np
import matplotlib.pyplot as plt
data = np.array([
                 [10.95, 11.18],               #使用array函数创建二维数组
                 [12.14, 10.43],
                 [13.22, 12.36],
                 [13.87, 14.15],
                 [15.06, 15.73],
                 [16.30, 16.40],
                 [17.01, 18.86],
                 [17.93, 16.13],
                 [19.01, 18.21],
                 [20.01, 18.37],
                 [21.04, 22.61],
                 [22.10, 19.83],
                 [23.17, 22.67],
                 [24.07, 22.70],
                 [25.00, 25.16],
                 [25.95, 25.55],
                 [27.10, 28.21],
                 [28.01, 28.12],
                 [29.06, 28.32],
                 [30.05, 29.18]
    ])
x = data[:,0]         #第一列数据为自变量x，一维数组
y = data[:,1]         #第二列数据为因变量y，一维数组
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.figure()
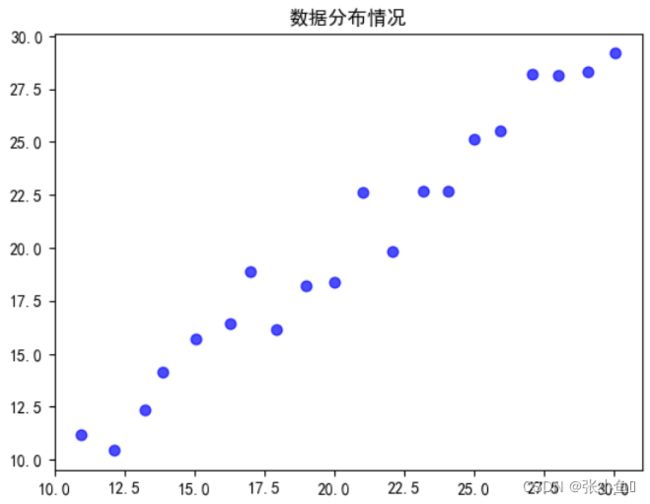
plt.scatter(x,y,s = 40,c = 'b',marker = 'o',alpha = 0.7)
plt.title('数据分布情况')
plt.show()

#第一种方法：按照一元线性回归公式进行计算
temp1_sum = 0.0
temp2_sum = 0.0
for i in range(0,20):
    temp1_sum+=x[i]
    temp2_sum+=y[i]
x_avg = temp1_sum/20
y_avg = temp2_sum/20
temp1_sum = 0
temp2_sum = 0
for i in range(0,20):
    temp_var = x[i]-x_avg
    temp1_sum=+temp_var*(y[i]-y_avg)
    temp2_sum=+temp_var**2
w = temp1_sum/temp2_sum
b = y_avg - w*x_avg
print('按照一元线性回归公式进行计算')
print('w = ',w)
print('b = ',b)

#在散点图的基础之上增加线性回归值线
x_lim = np.array([0,32])
y_pred = w * x_lim + b
plt.figure()
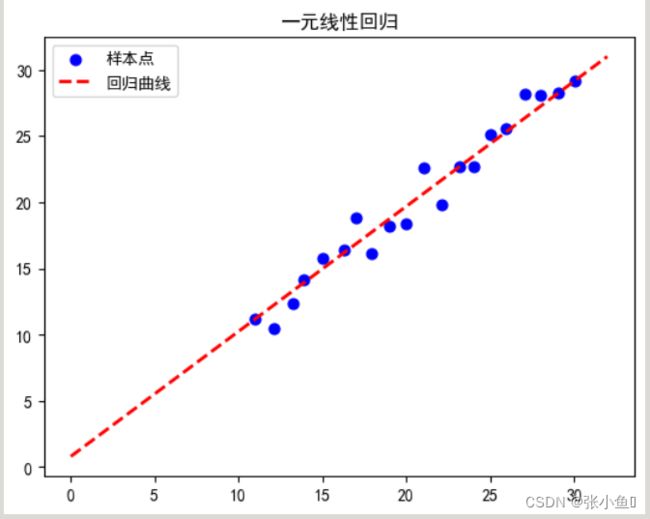
plt.scatter(x,y,s = 40,c = 'b',marker = 'o',label = '样本点')
plt.plot(x_lim,y_pred,ls = '--',lw = 2,color = 'r',label = '回归曲线')
plt.title('一元线性回归')
plt.legend()
plt.show()

#第二种方法：按照线性回归的向量形式进行计算
x_append = np.ones((20,2))
for i in range(0,20):
    x_append[i,0] = x[i]
temp1 = np.dot(x_append.T,x_append)
temp2 = np.linalg.inv(temp1)
temp3 = np.dot(temp2,x_append.T)
wb = np.dot(temp3,y)
print("使用向量形式计算的结果:",wb)

#第三种方法：采用scikit_learn中提供的标准回归函数进行计算
from sklearn import linear_model
#定义一个线性回归对象
lnr = linear_model.LinearRegression()
#训练模型
lnr.fit(x_append,y)#必须是二维数组
print('机器学习库函数计算结果：w:%s,b:%.6f'%(lnr.coef_,lnr.intercept_))

按照一元线性回归公式进行计算
w =  0.9446170044748614
b =  0.7942590155304146

使用向量形式计算的结果: [ 0.99397832 -0.22023935]
机器学习库函数计算结果：w:[0.99397832 0.        ],b:-0.220239

2.梯度下降法的使用

代码如下（示例）：

import numpy as np 
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
def costFunc(x):
    return 0.25*(x**4) - 2.167*(x**3)+6.25*x*x - 7*x
def gradFunc(x):
    return x**3 - 6.5*x**2 + 12.5*x -7
x = np.linspace(0,4.5,91)

#仅学习率的梯度下降法
step = 10
xPoint = np.empty(1,)
yPoint = np.empty(1,)
grad = np.empty(1,)
eta = 0.06
initPoint = 0.1
xPoint[0] = initPoint
yPoint[0] = costFunc(initPoint)
grad[0] = gradFunc(initPoint)
plt.figure(figsize = (4.5,4.5))
plt.plot(x,costFunc(x),'b',label = '代价函数')
for i in range(step):
    newPoint = xPoint[i] - eta * grad[i]
    xPoint = np.append(xPoint,newPoint)
    yPoint = np.append(yPoint,costFunc(newPoint))
    grad = np.append(grad,gradFunc(newPoint))
    xx = [xPoint[i],newPoint]
    yy = [yPoint[i],costFunc(newPoint)]
    plt.plot(xx,yy,color = 'r',linewidth = 1,linestyle = '--')
colors = ['green','c','b','k','g','pink','r','0.3','0.2','0.1','0.0']
plt.scatter(xPoint,yPoint,s = 40,color = colors,marker = 'o',label = '学习率$\\eta$={:.2f}'.format(eta))
plt.title("梯度下降法示意图",fontsize = 10)
plt.legend(loc = 'upper center',fontsize = 8)
plt.show()

3、批量梯度下降法

代码如下：

import numpy as np
import matplotlib.pyplot as plt
import time
start = time.time()
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
x=np.array([[10.0,1.0],[11,1],[12,1],[13,1],[14,1]])
y=np.array([20.0,23,25,27,26])
weight=np.empty((2,),float)
print('*******批量梯度下降法********')
def Loss(real,predict):
    return 0.5*np.power(np.dot(real-predict,real-predict),2)
def Cal(x,w):
    return np.matmul(x,w)
weight=np.random.random(np.shape(weight))
weight=[1.0,1.0]
loss_arr=np.empty([])
plt.scatter(x[:,0],y,s=20,marker='*')
eta=0.002
STEP=4
for step in range(STEP):
    if(step%1==0):
        plt.plot([9.5,14.5],[9.5*weight[0]+weight[1],14.5*weight[0]+weight[1]],label='第%d次'%(step))
        print('第%d次迭代'%(step+1))
        pred=Cal(x,weight)
        loss=Loss(y.T,pred)
        print('损失函数值为:%2f'%loss)
        loss_arr=np.append(loss_arr,loss)
        delta_w=eta*np.matmul((pred-y),x)
        weight-=delta_w
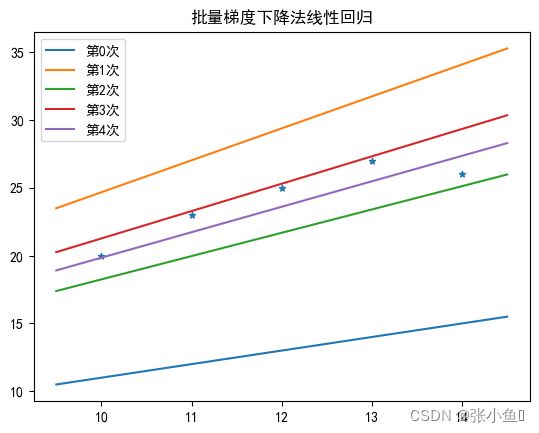
plt.plot([9.5,14.5],[9.5*weight[0]+weight[1],14.5*weight[0]+weight[1]],label='第%d次'%(STEP))
plt.title('批量梯度下降法线性回归')
plt.legend(loc='upper left')
plt.show()

*******批量梯度下降法********
第1次迭代
损失函数值为:202248.000000
第2次迭代
损失函数值为:10553.813310
第3次迭代
损失函数值为:682.582831
第4次迭代
损失函数值为:84.893686

4、多项式线性回归

代码如下：

#生成符合二次多项式特征的数据，并使用多项式回归进行拟合
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
from sklearn.linear_model import  LinearRegression
from sklearn.preprocessing import PolynomialFeatures#导入多项式特征模块
x = np.random.uniform(-3,3,size = 200)
X = x.reshape(-1,1)#转换为二维数据，与PolynomialFeatures匹配
y = 1.3*x**2 + 0.9*x + 4 +np.random.normal(0,0.8,size = 200)#生成y数据
plt.scatter(x,y,label = '含噪声样本')
degree = 2
poly = PolynomialFeatures(degree,include_bias = True)#定义多项式特征对象
#poly.fit(X,y)#计算多项式输出特征
#X2 = poly.transform(X)#转换多项式特征
X2 = poly.fit_transform(X,y)#与上面的一样
lr = LinearRegression()#定义线性回归对象
lr.fit(X2,y)#用转换后的多项式特征数据训练线性模型
y_predict = lr.predict(X2)
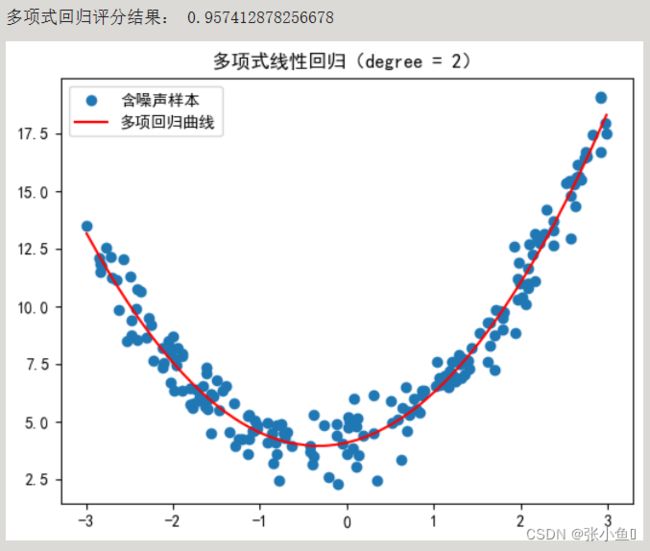
print('多项式回归评分结果：',lr.score(X2,y))
plt.plot(np.sort(x),y_predict[np.argsort(x)],'r',label = '多项回归曲线')
plt.title('多项式线性回归（degree = %d）'%degree)
plt.legend()
#np.sort(x)#返回x排序后的结果
#np.argsort(x)#返回x排序后的序号结果
plt.show()

 5、使用四种线性回归对波斯顿房价进行分析

波斯顿房价数据的属性说明：

CRIM--城镇人均犯罪率                                                              ------【城镇人均犯罪率】
ZN - 占地面积超过25,000平方英尺的住宅用地比例。               ------【住宅用地所占比例】
INDUS - 每个城镇非零售业务的比例。                                      ------【城镇中非商业用地占比例】
CHAS - Charles River虚拟变量（如果是河道，则为1;否则为0  ------【查尔斯河虚拟变量，用于回归分析】
NOX - 一氧化氮浓度（每千万份）                                             ------【环保指标】
RM - 每间住宅的平均房间数                                                      ------【每栋住宅房间数】
AGE - 1940年以前建造的自住单位比例                                     ------【1940年以前建造的自住单位比例 】
DIS -波士顿的五个就业中心加权距离                                        ------【与波士顿的五个就业中心加权距离】
RAD - 径向高速公路的可达性指数                                             ------【距离高速公路的便利指数】
TAX - 每10,000美元的全额物业税率                                          ------【每一万美元的不动产税率】
PTRATIO - 城镇的学生与教师比例                                             ------【城镇中教师学生比例】
B - 1000（Bk - 0.63）^ 2其中Bk是城镇黑人的比例                   ------【城镇中黑人比例】
LSTAT - 人口状况下降％                                                            ------【房东属于低等收入阶层比例】
MEDV - 自有住房的中位数报价, 单位1000美元                         ------【自住房屋房价中位数】

代码如下：

#使用四种线性回归对波斯顿房价做出分析
import numpy as np
np.set_printoptions(precision = 2)#设定输出为数组格式
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
import warnings
warnings.filterwarnings('ignore')
from sklearn import datasets
#导入sklearn中的线性模型与模型验证类
from sklearn import linear_model
from sklearn import model_selection
#加载房价数据
boston = datasets.load_boston()
#采用留出法划分数据集：测试集为30%
x_train,x_test,y_train,y_test = model_selection.train_test_split(boston.data,boston.target,test_size = 0.3,random_state =1)
lnr = linear_model.LinearRegression()#定义线性回归对象
rdr = linear_model.Ridge(alpha = 0.5#岭回归对象
lsr = linear_model.Lasso(alpha = 0.5)#定义套索回归对象,tol = le-5,max_iter = 10000
enet = linear_model.ElasticNet(alpha = 1.0,l1_ratio = 0.5)#定义弹性网络回归对象
#使用线性回归模型
lnr.fit(x_train,y_train)
w1 = lnr.coef_
b1 = lnr.intercept_
print("线性回归权重值：",w1)
print("线性回归偏置值：%.2f"%b1)
y_pred1 = lnr.predict(x_test)
var1 = np.mean((y_pred1-y_test)**2)
print("线性回归模型在测试集上的均方误差：%.2f"%(var1))
score1 = lnr.score(x_test,y_test)
print("线性回归模型在测试集上的评价得分：%.2f\n"%(score1))
#使用岭回归模型
rdr.fit(x_train,y_train)
w2 = lnr.coef_
b2 = lnr.intercept_
print("岭回归权重值：",w2)
print("岭回归偏置值：%.2f"%b2)
y_pred2 = rdr.predict(x_test)
var2 = np.mean((y_pred2-y_test)**2)
print("岭回归模型在测试集上的均方误差：%.2f"%(var2))
score2 = rdr.score(x_test,y_test)
print("岭回归模型在测试集上的评价得分：%.2f\n"%(score2))
#使用套索回归模型
lsr.fit(x_train,y_train)
print("套索回归权重值：",lsr.coef_)
print("套索回归偏置值：%.2f"%lsr.intercept_)
print("套索回归迭代步数：",lsr.n_iter_)
print("套索回归模型在测试集上的均方误差：%.2f"%(lsr.score(x_train,y_train)))
print("套索回归模型在测试集上的评价得分：%.2f\n"%(lsr.score(x_test,y_test)))
#使用zip函数分别对以上四个模型进行打包压缩
models = [lnr,rdr,lsr,enet]
names = ["线性回归","岭回归","套索回归","弹性网络"]
for model,name in zip(models,names):
    model.fit(x_train,y_train)
    print("权值为：{}".format(model.coef_))
    print("%s偏置值：%.2f"%(name,model.intercept_))
    y_pred = model.predict(x_test)
    var = np.mean((y_pred-y_test)**2)
    print("%s在测试集上的均方误差：{}"%(name).format(var))
    score = model.score(x_test,y_test)
    print("%s模型在测试集上的评价得分:%.2f\n"%(name,score))
#测试alpha在不同取值下的回归效果
scores = []
alphas = [0.0001,0.0005,0.001,0.005,0.01,0.05,0.1,0.5,1,5,10,50]
for index,model in enumerate(models):
    scores.append([])
    for alpha in alphas:
        if index>0:
            model.alpha = alpha
        model.fit(x_train,y_train)
        scores[index].append(model.score(x_test,y_test))
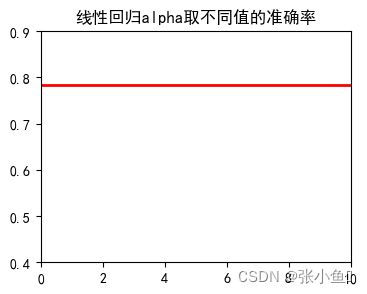
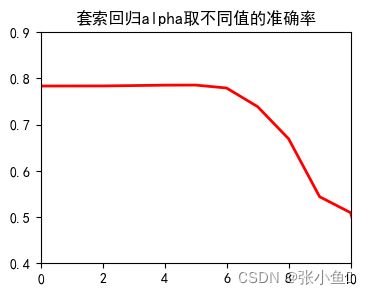
#以四种不同的图显示alpha1取值不同的准确率变化曲线
for i,name in enumerate(names):
    fig = plt.figure(i+1,figsize = (4,3))
    plt.xlim([0,10])
    plt.ylim([0.4,0.9])
    plt.plot(range(len(alphas)),scores[i],color = 'r',linewidth = 2)
    plt.title(name+'alpha取不同值的准确率')
    print("%s的准确率最大值：%.2f"%(name,max(scores[i])))
    plt.show()
#以子图显示alpha1取值不同的准确率变化曲线
fig = plt.figure(figsize=(10,7))
for i,name in enumerate(names):
    plt.subplot(2,2,i+1)
    plt.xlim([0,10])
    plt.ylim([0.4,0.9])
    plt.plot(range(len(alphas)),scores[i])
    plt.title(name+'alpha取不同值的准确率')
    print("%s的准确率最大值：%.2f"%(name,max(scores[i])))
plt.show()

线性回归权重值： [-9.85e-02  6.08e-02  5.92e-02  2.44e+00 -2.15e+01  2.80e+00  3.57e-03
 -1.52e+00  3.08e-01 -1.13e-02 -1.01e+00  6.45e-03 -5.69e-01]
线性回归偏置值：46.40
线性回归模型在测试集上的均方误差：19.83
线性回归模型在测试集上的评价得分：0.78

岭回归权重值： [-9.85e-02  6.08e-02  5.92e-02  2.44e+00 -2.15e+01  2.80e+00  3.57e-03
 -1.52e+00  3.08e-01 -1.13e-02 -1.01e+00  6.45e-03 -5.69e-01]
岭回归偏置值：46.40
岭回归模型在测试集上的均方误差：19.43
岭回归模型在测试集上的评价得分：0.79

套索回归权重值： [-0.07  0.06 -0.    0.   -0.    1.57  0.   -0.9   0.26 -0.01 -0.75  0.01
 -0.7 ]
套索回归偏置值：38.77
套索回归迭代步数： 50
套索回归模型在测试集上的均方误差：0.68
套索回归模型在测试集上的评价得分：0.74

权值为：[-9.85e-02  6.08e-02  5.92e-02  2.44e+00 -2.15e+01  2.80e+00  3.57e-03
 -1.52e+00  3.08e-01 -1.13e-02 -1.01e+00  6.45e-03 -5.69e-01]
线性回归偏置值：46.40
线性回归在测试集上的均方误差：{}
线性回归模型在测试集上的评价得分:0.78

权值为：[-9.28e-02  6.16e-02  2.83e-02  2.32e+00 -1.48e+01  2.87e+00 -1.97e-03
 -1.42e+00  2.92e-01 -1.19e-02 -9.26e-01  6.88e-03 -5.76e-01]
岭回归偏置值：41.48
岭回归在测试集上的均方误差：{}
岭回归模型在测试集上的评价得分:0.79

权值为：[-0.07  0.06 -0.    0.   -0.    1.57  0.   -0.9   0.26 -0.01 -0.75  0.01
 -0.7 ]
套索回归偏置值：38.77
套索回归在测试集上的均方误差：{}
套索回归模型在测试集上的评价得分:0.74

权值为：[-0.07  0.06 -0.    0.   -0.    0.61  0.02 -0.69  0.27 -0.01 -0.72  0.01
 -0.75]
弹性网络偏置值：43.50
弹性网络在测试集上的均方误差：{}
弹性网络模型在测试集上的评价得分:0.70

线性回归的准确率最大值：0.78 

岭回归的准确率最大值：0.79

套索回归的准确率最大值：0.79

弹性网络的准确率最大值：0.79

线性回归的准确率最大值：0.78
岭回归的准确率最大值：0.79
套索回归的准确率最大值：0.79
弹性网络的准确率最大值：0.79

 6、迭代算法

代码如下；

import sklearn.datasets as datasets
import numpy as np
from sklearn.linear_model import LogisticRegression as LR, LogisticRegression


class LogisticRegression():
    def __init__(self,alpha=0.01,epochs=3):
        self.W = None
        self.b = None
        self.alpha = alpha
        self.epochs = epochs

    def fit(self,X,y):
        self.W = np.random.normal(size=(X.shape[1]))
        self.b = 0
        for epoch in range(self.epochs):
            if epoch%100 == 1:
                print("********第%s次迭代********"%epoch)
                print("当前权值:",self.W)
                print("当前偏置值",self.b)
            w_derivate = np.zeros_like(self.W)
            b_derivate = 0
            for i in range(len(y)):
                w_derivate+=(y[i] -1/(1+np.exp(-np.dot(X[i],self.W.T)-self.b)))*X[i]
                b_derivate+=(y[i] -1/(1+np.exp(-np.dot(X[i],self.W.T)-self.b)))

            self.W = self.W + self.alpha*np.mean(w_derivate,axis=0)
            self.b = self.b + self.alpha*np.mean(b_derivate)
        return self

    def predict(self,X):
        p_1 = 1/(1+np.exp(-np.dot(X,self.W)-self.b))
        return np.where(p_1>0.5,1,0)

def accuracy(pred, true):
    count = 0
    for i in range(len(pred)):
        if (pred[i] == true[i]):
            count += 1
    return count / len(pred)

def normalize(x):
    return (x - np.min(x)) / (np.max(x) - np.min(x))

digits = datasets.load_breast_cancer()
X = digits.data
y = digits.target

print('数据集规模：', np.shape(X))
X_norm = normalize(X)
X_train = X_norm[:int(len(X_norm) * 0.7)]
X_test = X_norm[int(len(X_norm) * 0.7):]

y_train = y[:int(len(X_norm) * 0.7)]
y_test = y[int(len(X_norm) * 0.7):]

lr_self = LogisticRegression(epochs=500, alpha=0.03)
lr_self.fit(X_train, y_train)
y_pred = lr_self.predict(X_test)
print("自编逻辑斯蒂回归模型准确率：", accuracy(y_pred, y_test))

clf_lr = LR()
clf_lr.fit(X_train, y_train)
y_pred2 = clf_lr.predict(X_test)

print("机器学习库逻辑斯蒂回归模型准确率：", accuracy(y_pred2, y_test))

数据集规模： (569, 30)
********第1次迭代********
当前权值: [ 1.73956066 -0.01156931 -1.15917199  0.45711651  0.46040207 -0.01313549
  1.23924975  0.22666179  1.70779234 -0.49281854 -0.50133985  0.29592582
 -0.39109388 -2.17097176 -1.37779733 -0.5740774   0.05305788 -1.97634564
 -2.06258227  2.07302302 -0.85252618 -0.77235803 -0.19870169  0.04144355
 -0.54630171 -0.37447985 -0.50281008 -1.03194826 -0.43102844  0.42670525]
当前偏置值 0.6656184693726089
********第101次迭代********
当前权值: [-1.36236283 -3.1134928  -4.26109548 -2.64480697 -2.64152142 -3.11505898
 -1.86267374 -2.87526169 -1.39413115 -3.59474203 -3.60326334 -2.80599767
 -3.49301737 -5.27289525 -4.47972081 -3.67600089 -3.0488656  -5.07826912
 -5.16450575 -1.02890047 -3.95444967 -3.87428152 -3.30062518 -3.06047994
 -3.6482252  -3.47640334 -3.60473357 -4.13387175 -3.53295192 -2.67521824]
当前偏置值 4.2264662880627215
********第201次迭代********
当前权值: [-3.64541622 -5.39654619 -6.54414888 -4.92786037 -4.92457482 -5.39811237
 -4.14572713 -5.15831509 -3.67718455 -5.87779542 -5.88631674 -5.08905107
 -5.77607076 -7.55594865 -6.76277421 -5.95905428 -5.331919   -7.36132252
 -7.44755915 -3.31195387 -6.23750307 -6.15733491 -5.58367858 -5.34353333
 -5.93127859 -5.75945674 -5.88778696 -6.41692514 -5.81600532 -4.95827163]
当前偏置值 4.450665474290417
********第301次迭代********
当前权值: [-5.05721197 -6.80834194 -7.95594463 -6.33965612 -6.33637057 -6.80990812
 -5.55752288 -6.57011084 -5.0889803  -7.28959117 -7.29811248 -6.50084682
 -7.18786651 -8.96774439 -8.17456996 -7.37085003 -6.74371475 -8.77311827
 -8.8593549  -4.72374962 -7.64929882 -7.56913066 -6.99547433 -6.75532908
 -7.34307434 -7.17125249 -7.29958271 -7.82872089 -7.22780107 -6.37006738]
当前偏置值 4.041335598886869
********第401次迭代********
当前权值: [-5.95660858 -7.70773855 -8.85534123 -7.23905273 -7.23576717 -7.70930473
 -6.45691949 -7.46950745 -5.9883769  -8.18898778 -8.19750909 -7.40024343
 -8.08726312 -9.867141   -9.07396657 -8.27024664 -7.64311136 -9.67251488
 -9.75875151 -5.62314622 -8.54869542 -8.46852727 -7.89487094 -7.65472569
 -8.24247095 -8.0706491  -8.19897932 -8.7281175  -8.12719768 -7.26946399]
当前偏置值 3.5836074309001096
自编逻辑斯蒂回归模型准确率： 0.9532163742690059
机器学习库逻辑斯蒂回归模型准确率： 0.935672514619883

---

总结

以上就是今天要讲的内容，本文仅仅简单介绍了机器学习当中几种基本算法，希望对初学者的你有所帮助。

最后欢迎大家点赞，收藏⭐，转发，
如有问题、建议，请您在评论区留言哦。