【算法】最直接的算法——穷举法详解

第三章 穷举法

一、基本概念

穷举法又称为枚举法或者蛮力法，是一种简单直接解决问题的方法，常常是基于问题的直接描述去编写程序，比如说求n的阶乘，那么就直接一个循环n次的for循环。

穷举法依赖的基本技术是遍历，也就是采用一定策略依次处理待求解问题的所有元素。对于穷举法自身的优化，一般只能减少其执行的系数，但是数量级不会改变。由于穷举法需要遍历所有元素，因此他的时间性能往往是最低的，指数级的时间开销往往都是采用穷举带来的，但是它依旧是很重要的算法设计思想，因为：

• 理论上，穷举法可以解决许多计算领域的问题（只要机器性能足够或者时间开销可承受）。并且在一些较为基本的问题的求解中运用十分广泛，比如求n个数的和。
• 穷举法可以用于解决一些规模较小的问题，因为其时间规模在可承受范围内
• 对于某方面的问题（比如排序、查找、串匹配），可以基于穷举法设计出一些优化算法，这些优化算法是可用并且具有实用价值的，比如说KMP算法就是基于穷举法优化的串匹配算法
• 穷举可以作为某类问题的时间性能下界，来衡量同样问题其他算法是否具有更高效率。

下列是一个经典穷举问题：

我们知道，假设有i张10元，j张5元，k张1元，那么满足兑换方案的方程应该是$i+j+k=50$并且$i\ast 10+j\ast 5+k=100$。而10元最多5张，5元最多10张，1元最多50张。按照上述编程可得：

class Main {
    public static void main(String[] args) {
        int sum = 0;
        for (int i = 0; i < 10; i++) {
            for (int j = 0; j < 20; j++) {
                for (int k = 0; k < 100; k++) {
                    if (i * 10 + j * 5 + k == 100 && i + j + k == 50){
                        System.out.printf("%d %d %d\n", i, j, k);
                        sum++;
                    }
                }
            }
        }
        System.out.println(sum);
    }
}

二、查找中的穷举法

查找是穷举法应用十分重要的一个领域，虽然穷举十分笨拙，但是只要规模不大，还是可行的

2.1 顺序匹配

顺序查找是基于穷举的查找法。在一个有n个元素的一维的顺序表中，从第0个元素开始逐个向下查找，如果找到目标值则直接返回目标值的下标；否则继续查找下一个元素，直到n个元素均被遍历完。分析时间开销：最好的情况，也就是需要查找的元素刚好是0号元素，时间开销为O(1)；最坏情况，也就是顺序表中没有目标值，需要遍历n个元素，时间开销O(n)；平均需要遍历n/2个元素，时间开销还是O(n)

2.2 串匹配问题

简单的模式匹配算法

子串的定位操作称为串的模式匹配，其中简单的模式匹配算法是一种不依赖其他串操作的暴力匹配算法。其算法思想是，将主串中和模式串等长的子串全部提取出来，并且依次对比。

暴力模式匹配算法的最坏时间复杂度为O(nm),最好的时间复杂度为O(m)，其中n，m分别为主串和模式串的长度。

改进的模式匹配算法——KMP算法

在暴力匹配算法中，每次匹配失败都是后移一位再从头开始比较，但是比如：

在 a b a b c a b c a c 中查找abcac

这会导致一定的重复比较，从而导致效率下降（展开说）

1.字符串的前缀、后缀和部分匹配值

前缀指的是出最后一个字符外所有的头部子串，后缀指的是除第一个字符外字符串的所有尾部子串；部分匹配值为字符串的前缀和后缀的最长相等前后缀长度。

在对比到第k个字符时，如果发生了串不匹配，可以寻找已匹配的串的最大公共前后缀，从而使得不需要重复对比。

在一个有n个字符的串中，可能存在n种匹配失败的情景，对应的是n种部分匹配串。每一种部分匹配串的最大前后缀是固定的，因此可以提前计算出对比到k个字符错配时主串需要前进的步数，并且将其存储在next数组中。这样在KMP算法执行时，可以直接使用

重点：next数组的计算

最长相等前后缀长度可以使得主串不需要回退，故KMP算法可以在O(n+m)的时间数量级上完成串的模式匹配操作，提高了模式匹配效率。其中，O(m)的时间复杂度是在求next数组时产生的，O(n)的时间复杂度是在执行KMP算法时产生的。

总的来说，相对于朴素模式匹配算法，KMP算法能够避免主串指针频繁回溯，从而提高了效率

2.KMP算法的原理是什么

当子串与扫描到的主串不匹配的时候，首先计算出已匹配的子串的前缀和后缀的最大公共子集。然后可以将子串向后移动，将共有前缀移动到原子集的共有后缀处，从而避免重复查找，使得子串不需要回退。

右移位数 = 已匹配的字符数 - 对应的部分字符值

3.KMP算法的进一步优化
KMP算法在对比诸如"aaaab"这类串的时候，还是会出现重复匹配的问题，为了解决而需要在next数组的基础上再进一步处理得到nextval数组。

三、排序问题中的穷举法

排序问题指的是如何将乱序的序列排列成元素有序的序列

3.1 选择排序

选择排序的基本思想是：每一趟在后面n-i+1个待排序元素中选取关键字最小的元素，作为有序子序列的第i个元素，直到第n-1趟做完，待排元素只剩下一个，就不用再选了。

假设排序表为L[1…n]，第i趟从L[i…n]中选择关键字最小的元素与L(i)交换，每趟排序可以确定一个元素的最终位置，这样经过n-1趟排序就可以使得整个排序表。

具体步骤如下：

1. 将整个顺序表划分为有序区和无序区，初始时有序区为空，无序区含有所有元素
2. 在无序区查找值最小的元素，将它和无序区的第一个元素交换，使得有序区扩展一个元素，无序区减少一个元素
3. 不断重复上述步骤，直到计生一个记录为止

空间效率：只使用常数个辅助单元，空间效率为O(1)

时间效率：简单选择排序中，元素移动操作次数很少，不会超过3(n-1)次，最好情况是移动0次。但是元素间比较次数和序列初始状态无关，都是n(n-1)次，因此时间复杂度为O(n²)

该算法不稳定，可用顺序表和链表表示

3.2 冒泡排序

从后往前两两比较元素的值，如果逆序则交换两个元素的值，每一趟排序都可以将一个元素移动到最终位置，已经确定好位置的元素无需对比。如果在某一趟中没有发生交换，那么证明剩余序列已经有序，可以提前结束了。

// 冒泡排序
void swap(int &a, int &b){
    int temp = a;
    a = b;
    b = temp;
}

void bubbleSort(int a[], int n){
    for (int i = 0; i < n - 1; ++i) {
        bool flag = false; // 是否发生交换的标志
        for (int j=n-1; j>i; j--){ // 一趟冒泡的
            if (a[j-1]>a[j]){   // 如果是逆序
                swap(a[j-1], a[j]);
                flag = true;
            }
        }
        if (!flag)
            return;
    }
}

性能：
空间复杂度：O(1)
时间复杂度:
最好情况是有序的，为O(n)；最坏情况为逆序，需要交换$\frac{n(n-1)}{2}$为O(n²)；平均的复杂度也是O(n²)
冒泡排序是稳定的，适用于链表。

四、组合问题中的穷举法

01背包问题

问题：给定n个重量为{w1,w2,…wn}，价值为{v1,v2,…vn}的物品和一个容量为C的背包，如何装入物品使得背包中的物品价值最大。

思想：穷举法解决01背包其实就是遍历n个物品集合的所有组合，找出总重量不超过背包的组合集中价值最大的组合。比如有3个物品的所有组合有{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}

开销：对于有n个物品的01背包问题，采用穷举法需要消耗O(n²)的时间，虽然可以采用一定的剪枝措施，比如如果发现放入{1,2}就已经超重了，那么凡事含有{1,2}的集合都会超重（比如说{1,2,3})，这些集合就不需要再进行遍历。但是这只能减少它的执行系数，但是数量级不会改变，仍然是O(n²)。

任务分配问题

问题描述：
任务分配问题中，会有n个任务和m个人，每个任务只分配给一个人，每个人只执行一个任务，第i个人执行第j个任务分配的开销为C_ij。任务分配问题的目标是找出开销最小的分配序列。

分析：
根据描述，可以使用一个n*m的二维数组存储信息，第i行第j列表示第i个人执行第j个任务所需的花销。而任务分配问题就是选择n行中的一个元素，代表选出n个人并且给他们分配一个任务。这些被分配到任务的人可以组成一个n个元素的顺序表alloc，其中alloc[i]表示第i个人被分配到了第alloc[i]个任务。比如说{2,1,3}表示第一个人被分配到第2个任务，第二个人被分配到第1个任务，第三个人被分配到了第三个任务。穷举法其实就是遍历alloc表的所有组合，从中选取开销最小的组合。这类似于找到组合的全排列

开销：任务分配问题的全排列的时间开销为n!，这意味着除非问题规模很小，否则时间开销都是难以承受的。

五、图问题中的穷举法

哈密顿回路问题

哈密顿回路问题中，有n座城市，要求从某一个城市出发，只经过每个城市一次，然后回到出发的城市。如果存在这种路径则称之为哈密顿回路。

分析：
n个城市可以看作一个有n个结点的无向图G，而城市之间的路径就是图中的边。穷举法求哈密顿回路的基本思路是，对于无向图G，依次将图中所有顶点进行全排列，满足以下两个条件的全排列构成的回路就是哈密顿回路：

• 相邻顶点之间存在边
• 最后一个顶点和第一个顶点之间存在边

开销：
哈密顿算法只需要找到一条符合的边就可以结束算法， 可能并不需要遍历所有全排列，但是最坏情况是不存在哈密顿回路，这种情况必须遍历所有全排列，时间复杂度为O(n!)

TSP问题

TSP问题又称为旅行家问题，旅行家要去n个城市旅游，然后返回处罚的城市，要求各个城市只经过一次并且所走的路径最短。

分析：
n个城市可以看作一个有n个结点的无向图G，和哈密顿回路不同的是，哈密顿中的图并非为有权图。穷举法找最短路径，首先是找出所有顶点的全排列，然后找出所有路径汇总的哈密顿回路。对比各个哈密顿回路，选出其中最短的哈密顿回路。其求解方法其实和哈密顿回路较为相似

开销：
任何情况下都需要遍历全排列，因此时间开销固定为O(n!)

六、几何问题中的穷举法

最近点对问题

在一个二维平面上有n个点，需要找出这n个点中距离最近的一对点

分析：
穷举法都很暴力，遍历所有的点对，并且使用$\sqrt{x^2+y^2}$求出距离，然后最终得出最短距离。其时间复杂度为O(n^2)

凸包问题

定义1:
对于平面上一个点的有限集合，如果集合中任意的两个点P和Q连成的线段上的所有点都位于集合内，则称该集合为凸集合。比如：

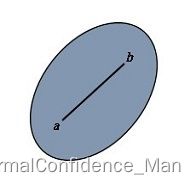
很显然，圆形和正方形都是凸集合，而下列图形则显然不是凸集合

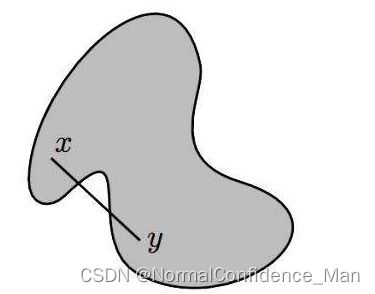
一个点集S的凸包是包含S的最小凸集合，其中最小是指S的凸包一定是所有包含S的凸集合的子集