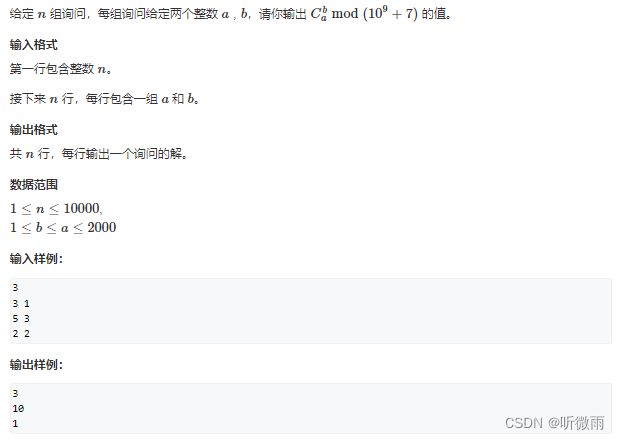
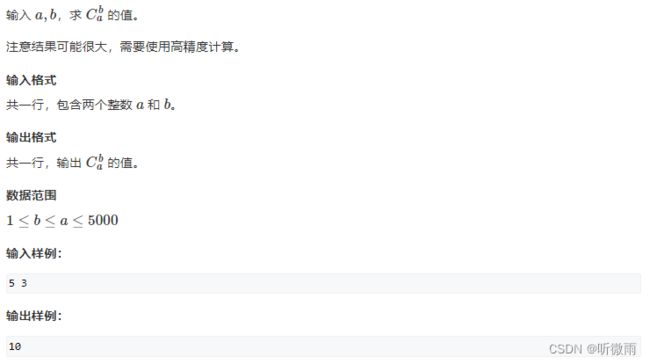
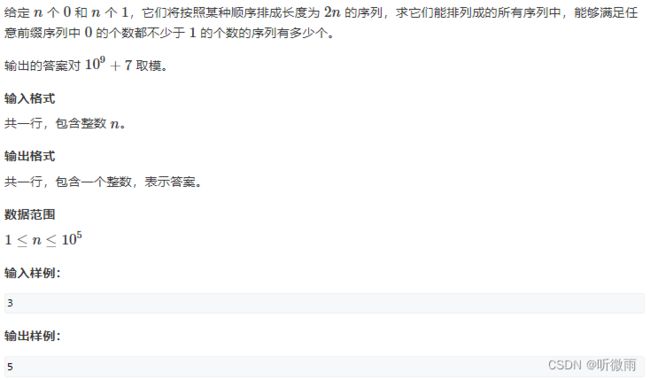
求组合数（数论）

求组合数Ⅰ

题解

基于数据范围，我们可以先把相应数据初始化出来。
存在如下公式：
$C_a^b=C_{a-1}^b+C_{a-1}^{b-1}$
从$a$个人中选$b$个人出来，可以分为包含小明和不包含小明的情况。
包含小明：$C_{a-1}^{b-1}$；不包含小明：$C_{a-1}^b$
相当于Dp状态转移的过程

import java.io.*;

public class Main{
    static int N=2010;
    static int mod=(int)(1e9+7);
    static int[][] c=new int[N][N];
    public static void main(String[] args)throws IOException{
        BufferedReader in=new BufferedReader(new InputStreamReader(System.in));
        int n=Integer.parseInt(in.readLine());
        init();
        String[] strs;
        for(int i=0;i<n;i++){
            strs=in.readLine().split(" ");
            int a=Integer.parseInt(strs[0]);
            int b=Integer.parseInt(strs[1]);
            System.out.println(c[a][b]);
        }
    }
    static void init(){
        for(int i=0;i<N;i++){
            for(int j=0;j<=i;j++){
                if(j==0)c[i][j]=1; //从i个中选0个有1种方案
                else c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
            }
        }
    }
}

求组合数Ⅱ

题解

基于本题$a,b$的数据范围，$1\le b\le a\le 10^5$，我们可以先把相应数据初始化出来。
用如下公式将数据提前初始化：
$C_a^b=\frac{a!}{(b-a)!b!}$
因为$a!modp=1modp\times 2modp\times 3modp\times ...\times (a-1)modp\times amodp$
但是$\frac{a!modp}{b!modp}\ne \frac{a!}{b!}modp$
这里可以用逆元来解决这个问题
$\frac{a!}{b!}modp=a!b{!}^{-1}modp$

逆元也存在以下情况：
$b{!}^{-1}modp=1^{-1}modp\times 2^{-1}modp\times 3^{-1}modp\times ...\times (b-1{)}^{-1}modp\times b^{-1}modp$
证明，假设$a$是$x$的逆元，$ax=1$，$b$是$y$的逆元，$by=1$，所以$abxy=1$，所以$ab$是$xy$的逆元
求逆元可看：
https://blog.csdn.net/m0_54136420/article/details/128311218?spm=1001.2014.3001.5502

import java.io.*;

public class Main{
    static int N=100010;
    static long[] fact=new long[N];
    static long[] infact=new long[N];
    static int mod=(int)(1e9+7);
    public static void main(String[] args)throws IOException{
        BufferedReader in=new BufferedReader(new InputStreamReader(System.in));
        
        fact[0]=1;
        infact[0]=1;
        for(int i=1;i<N;i++){
            fact[i]=fact[i-1]*i%mod;
            infact[i]=infact[i-1]*qmi((long)i,mod-2,mod)%mod;
        }
        
        String[] strs=in.readLine().split(" ");
        int n=Integer.parseInt(strs[0]);
        for(int i=1;i<=n;i++){
            strs=in.readLine().split(" ");
            int a=Integer.parseInt(strs[0]);
            int b=Integer.parseInt(strs[1]);
            System.out.println(fact[a]*infact[a-b]%mod*infact[b]%mod);
        }
    }
    static long qmi(long a,int k,int p){
        long res=1;
        while(k!=0){
            if((k&1)==1)res=(res*a)%p;
            k>>=1;
            a=a*a%p;
        }
        return res;
    }
}

求组合数Ⅲ

题解

基于本题的数据范围。可以考虑用卢卡斯定理
卢卡斯定理公式：
$C_a^b\equiv C_{amodp}^{bmodp}\cdot C_{a/p}^{b/p}(modp)$
证明：
令$a=a_k\cdot p^k+a_{k-1}\cdot p^{k-1}+\cdots +a_0\cdot p^0$ ①
$b=b_k\cdot p^k+b_{k-1}\cdot p^{k-1}+\cdots +b_0\cdot p^0$ ②

$(1+x{)}^p=C_p^0\cdot 1+C_p^{1}x+C_p^2{x}^2+\cdots +C_p^p{x}^p$ ③
因为$C_p^1,C_p^2,...,C_p^{p-1}$中分子都含有$p$，所以mod p都等于0
故$(1+x{)}^p=C_p^0\cdot 1+C_p^{1}x+C_p^2{x}^2+\cdots +C_p^p{x}^p\equiv 1+x^p(modp)$

$(1+x{)}^a=(1+x{)}^{a_0}\cdot ((1+x{)}^p{)}^{a_1}\cdot ((1+x{)}^{p^2}{)}^{a_2}\cdots ((1+x{)}^{p^k}{)}^{a_k}$
$\equiv (1+x{)}^{a_0}\cdot (1+x^p{)}^{a_1}\cdot (1+x^{p^2}{)}^{a_2}\cdots (1+x^{p^k}{)}^{a_k}(modp)$

$(1+x{)}^a$中包含$x^b$的常数项为$C_a^b$
根据②和③可得，该$(1+x{)}^{a_0}\cdot (1+x^p{)}^{a_1}\cdot (1+x^{p^2}{)}^{a_2}\cdots (1+x^{p^k}{)}^{a_k}$中包含$x^b$的常数项是$C_{a_k}^{b_k}\cdot C_{a_{k-1}}^{b_{k-1}}\cdots C_{a_0}^{b_0}(modp)$

综上$C_a^b\equiv C_{a_k}^{b_k}\cdot C_{a_{k-1}}^{b_{k-1}}\cdots C_{a_0}^{b_0}(modp)$
即$C_a^b\equiv C_{amodp}^{bmodp}\cdot C_{a/p}^{b/p}(modp)$

不清楚$C_a^b\equiv C_{a_k}^{b_k}\cdot C_{a_{k-1}}^{b_{k-1}}\cdots C_{a_0}^{b_0}(modp)$和$C_a^b\equiv C_{amodp}^{bmodp}\cdot C_{a/p}^{b/p}(modp)$为啥相等的，看下面：
根据①$a=a_k\cdot p^k+a_{k-1}\cdot p^{k-1}+\cdots +a_0\cdot p^0$得，$amodp=a_0$
同理$bmodp=b_0$,所以$C_{amodp}^{bmodp}=C_{a_0}^{b_0}$

然后相当于$C_a^b=C_{a_0}^{b_0}\cdot C_{a/p}^{b/p}(modp)$，$C_{a/p}^{b/p}=C_{a/pmodp}^{b/pmodp}\cdot C_{a/p^2}^{b/p^2}$
根据①得$C_{a/pmodp}^{b/pmodp}=C_{a_1}^{b_1}$,所以$C_a^b=C_{a_0}^{b_0}\cdot C_{a_1}^{b_1}\cdot C_{a/p^2}^{b/p^2}$,不断递归，最后得到：
$C_a^b\equiv C_{a_k}^{b_k}\cdot C_{a_{k-1}}^{b_{k-1}}\cdots C_{a_0}^{b_0}(modp)$

import java.io.*;

public class Main{
    static long p;
    public static void main(String[] args)throws IOException{
        BufferedReader in=new BufferedReader(new InputStreamReader(System.in));
        String[] strs=in.readLine().split(" ");
        int n=Integer.parseInt(strs[0]);
        for(int i=0;i<n;i++){
            strs=in.readLine().split(" ");
            long a=Long.parseLong(strs[0]);
            long b=Long.parseLong(strs[1]);
            p=Long.parseLong(strs[2]);
            System.out.println(lucas(a,b));
        }
    }
    static long lucas(long a,long b){
        if(a<p&&b<p)return C(a,b)%p;
        return (C(a%p,b%p)*lucas(a/p,b/p))%p;
    }
    static long C(long a,long b){
        if(a<b)return 0;
        long res=1;
        for(long i=1,j=a;i<=b;i++,j--){
            res=res*j%p;
            res=res*qmi(i,p-2)%p;
        }
        return res;
    }
    static long qmi(long a,long k){
        long res=1;
        while(k!=0){
            if((k&1)==1)res=res*a%p;
            k>>=1;
            a=a*a%p;
        }
        return res;
    }
}

求组合数Ⅳ

题解

$$\begin{gathered} \begin{array}{rl}{C}_a^b& =\frac{a\times (a-1)\times ...\times (a-b+1)}{b\times (b-1)\times ...\times 1}\\ & =\frac{a\times (a-1)\times ...\times (a-b+1)\times (a-b)!}{b\times (b-1)\times ...\times 1\times (a-b)!}\\ & =\frac{a!}{b!(a-b)!}\end{array} \\ 分解质因数:C_a^b=p_1^{a_1}{p}_2^{a_2}\cdots p_k^{a_k} \\ \begin{array}{rl}求a！分解p的次数sum[p]& =\lfloor \frac{a}{p}\rfloor +\lfloor \frac{a}{p^2}\rfloor +\lfloor \frac{a}{p^3}\rfloor +\cdots \\ & =p的倍数在[1,a]中的个数+p^2的倍数在[1,a]中的个数+...\end{array} \\ 比如求8！=1\times 2\times 3\times 4\times 5\times 6\times 7\times 8中2的个数。 \\ 1到8之间2的一次方有2、4、6、8四个2 \\ 含2的二次方有4、8，但4、8中2的一次方已经记过一次了,所以只加二次方中的两个2 \\ 含2的三次方有8，但8中的一次、二次方都被记过一次了，所以只加二次方中的一个2 \\ 根据消除质因数，C_a^b中p的出现次数为： \\ a！中出现的p的次数-(a-b)！中出现p的次数-b!中p出现的次数 \end{gathered}$$
因为没有$mod$一个大数，所以这里要用高精度相乘，同时还要提前初始化质数。

import java.io.*;
import java.math.BigInteger;

public class Main{
    static int N=5010;
    static boolean[] st=new boolean[N];
    static int[] primes=new int[N];
    static int cnt;
    static int[] sum=new int[N];
    public static void main(String[] args)throws IOException{
        BufferedReader in=new BufferedReader(new InputStreamReader(System.in));
        String[] strs=in.readLine().split(" ");
        int a=Integer.parseInt(strs[0]);
        int b=Integer.parseInt(strs[1]);
        get_primes(a);
        
        for(int i=0;i<cnt;i++){
            int p=primes[i];
            sum[i]=get(a,p)-get(a-b,p)-get(b,p);
        }
        
        BigInteger res=new BigInteger("1");
        for(int i=0;i<cnt;i++){
            int p=primes[i];
            for(int j=0;j<sum[i];j++){
                res=res.multiply(new BigInteger(String.valueOf(p)));
            }
        }
        System.out.println(res);
    }
    static void get_primes(int n){
        for(int i=2;i<=n;i++){
            if(!st[i])primes[cnt++]=i;
            for(int j=0;primes[j]<=n/i;j++){
                st[primes[j]*i]=true;
                if(i%primes[j]==0)break;
            }
        }
    }
    static int get(int n,int p){
        int res=0;
        while(n>0){
            res+=n/p;
            n/=p;
        }
        return res;
    }
}

满足条件的01序列

题解

将 01 序列置于坐标系中，起点定于原点。若 0 表示向右走，11表示向上走，那么任何前缀中 0 的个数不少于 1 的个数就转化为，路径上的任意一点，横坐标大于等于纵坐标。题目所求即为这样的合法路径数量。
下图中，表示从 (0,0) 走到 (n,n) 的路径，在绿线及以下表示合法，若触碰红线即不合法。

由图可知，任何一条不合法的路径（如黑色路径），都对应一条从 (0,0) 走到 (n−1,n+1) 的一条路径（如灰色路径）。而任何一条 (0,0)走到 (n−1,n+1)的路径，也对应了一条从 (0,0)走到 (n,n)的不合法路径。
来源：https://www.acwing.com/solution/content/8907/
卡特兰数：
$$\begin{array}{rl}{C}_{2n}^n-C_{2n}^{n-1}& =\frac{(2n)!}{n!n!}-\frac{(2n)!}{(n-1)!(n+1)!}\\ & =\frac{(2n)!(n+1)-(2n)!n}{(n+1)!n!}\\ & =\frac{(2n)!}{(n+1)!n!}\\ & =\frac{1}{n+1}\frac{(2n)!}{n!n!}\\ & =\frac{1}{n+1}{C}_{2n}^n\end{array}$$

import java.io.*;

public class Main{
    static int mod=(int)(1e9+7);
    public static void main(String[] args)throws IOException{
        BufferedReader in=new BufferedReader(new InputStreamReader(System.in));
        long n=Integer.parseInt(in.readLine());
        long res=1;
        for(long i=2*n,j=1;j<=n;j++,i--){
            res=res*i%mod;
            res=res*get(j,mod-2,mod)%mod;
        }
        System.out.println(res*get(n+1,mod-2,mod)%mod);
    }
    static long get(long a,long k,long p){
        long res=1;
        while(k>0){
            if((k&1)==1)res=res*a%p;
            k>>=1;
            a=a*a%p;
        }
        return res;
    }
}