数据结构与算法
数据结构与算法
数据结构(英语:data structure)是计算机中存储、组织数据的方式。
数据结构是一种具有一定逻辑关系,在计算机中应用某种存储结构,并且封装了相应操作的数据元素集合。它包含三方面的内容,逻辑关系、存储关系及操作。
不同种类的数据结构适合于不同种类的应用,而部分甚至专门用于特定的作业任务。例如,计算机网络依赖于路由表运作,B 树高度适用于数据库的封装。
一、线性表
线性表是最基本、最简单、也是最常用的一种数据结构。线性表(linear
list)是数据结构的一种,一个线性表是n个具有相同特性的数据元素的有限序列。
1、运行结果
2、具体代码
#include 二、顺序栈
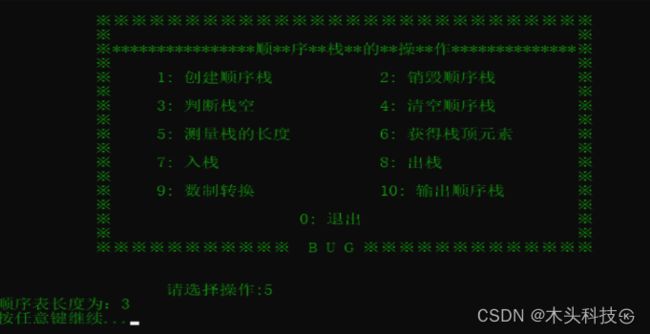
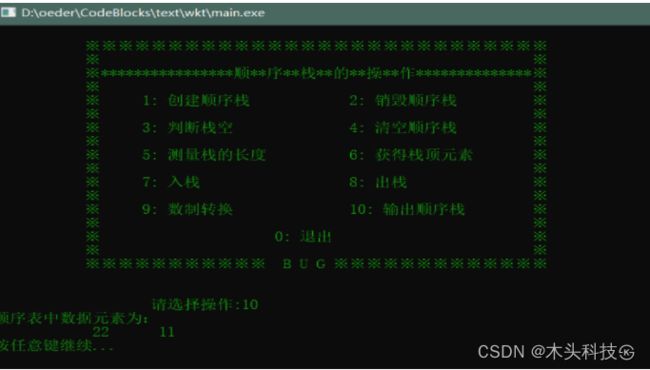
顺序栈是栈的顺序实现。顺序栈是指利用顺序存储结构实现的栈。采用地址连续的存储空间(数组)依次存储栈中数据元素,由于入栈和出栈运算都是在栈顶进行,而栈底位置是固定不变的,可以将栈底位置设置在数组空间的起始处;栈顶位置是随入栈和出栈操作而变化的,故需用一个整型变量top来记录当前栈顶元素在数组中的位置。
1、运行结果
2、具体代码
#include三、链表
链表是一种物理存储单元上非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列结点(链表中每一个元素称为结点)组成,结点可以在运行时动态生成。每个结点包括两个部分:一个是存储数据元素的数据域,另一个是存储下一个结点地址的指针域。
相比于线性表顺序结构,操作复杂。由于不必须按顺序存储,链表在插入的时候可以达到O(1)的复杂度,比另一种线性表顺序表快得多,但是查找一个节点或者访问特定编号的节点则需要O(n)的时间,而线性表和顺序表相应的时间复杂度分别是O(logn)和O(1)。
1、运行结果
2、具体代码
#include "stdio.h"
#include "malloc.h"
typedef int ElemType;
typedef struct LNode{
ElemType data; //数据域
struct LNode *next; //指针域
}LNode,*LinkStack; //栈类型定义
//初始化链栈
void InitStack(LNode *lst){
//申请头结点
lst = (LNode *)malloc(sizeof(LNode));
//指针域置空
lst->next = NULL;
}
//判断链栈是否为空
int IsEmpty(LNode lst){
//判断头结点的指针域是否为空
if(lst.next == NULL){
return 1;
}
else{
return 0;
}
}
//入栈
void push(LNode *lst,ElemType n){
LNode *p;
int i;
//为新的结点申请空间
p = (LNode *)malloc(sizeof(LNode));
for(i = 0;i<n;i++){
//为数据域赋值
scanf("%d",&p->data);
}
//将新插入的结点指向原来的栈顶结点
p->next = lst->next;
//头结点指向新入栈的结点
lst->next = p;
}
//出栈
int pop(LNode *lst,ElemType *x){
//判断链栈是否为空
if(lst->next == NULL){
return 0;
}
LNode *p;
//获取出栈结点
p = lst->next;
//获取出栈结点的数据域
*x = p->data;
//出去栈顶元素
lst->next = p->next;
//释放栈顶元素
free(p);
return 1;
}
//获取栈顶元素
int GetTop(LNode *lst) {
//判断头结点的指针域是否为空
if(lst->next!=NULL){
return lst->next->data;
}
}
int main(){
LNode lst;
int i;
int x;
int j;
//初始化
InitStack(&lst);
printf("\n");
printf("请输入入栈元素的个数:\n");
scanf("%d",&i);
printf("请输入入栈元素:\n");
push(&lst,i);
printf("目前栈顶元素为:");
printf("%d",GetTop(&lst));
printf("\n");
printf("第一个出栈的元素为:");
pop(&lst,&x);
printf("%d",x);
}
四、顺序队列
顺序队列是队列的顺序存储结构,顺序队列实际上是运算受限的顺序表。和顺序表一样,顺序队列用一个向量空间来存放当前队列中的元素。由于队列的队头和队尾的位置是变化的,设置两个指针front和rear分别指示队头元素和队尾元素在向量空间中的位置,它们的初值在队列初始化时均应设置为0。
1、运行结果
2、具体代码
#define MAXQSIZE 100
typedef struct
{ int base[MAXQSIZE];
int front;
int rear;
} Sqqueue;
Sqqueue enqueue(Sqqueue Q,int e)/*队列的入队函数*/
{ if ((Q.rear+1)%MAXQSIZE==Q.front)
printf("ERROR\n");
else
{Q.base[Q.rear]=e;
Q.rear = (Q.rear+1)%MAXQSIZE; //队尾指针+1
}
return Q;
}
Sqqueue dequeue(Sqqueue Q,int *e)/*队列的出队函数*/
{ int x;
if (Q.front==Q.rear)
printf("ERROR\n ");
else
{ e=Q.base[Q.front]; //保存队头元素
Q.front=(Q.front+1)%MAXQSIZE;//对头指针+1
}
return Q;
}
void display(Sqqueue Q)/*队列元素输出函数*/
{ int k,m;
k=Q.front;m=Q.rear;
while(k!=m)
{ printf("%4d",Q.base[k]);
k=(k+1)%MAXQSIZE;}
printf("\n");
}
main()/*主函数*/
{ Sqqueue Q;
int i,n,x,y,e;
Q.rear=Q.front=0; /*初始化顺序队列,使其成为空队列*/
printf("\nplease input the length:");/*请求输入队列的长度*/
scanf("%d",&n);
printf("please input create data:\n ");/*请求输入队列中各个元素*/
for(i=1;i<=n;i++)
{scanf("%d",&x);
Q=enqueue(Q,x);}/*调用队列插入函数*/
printf("the queue is:\n");
display(Q);/*调用队列元素输出函数*/
printf("please input a insert data:");/*请求输入需要插入的元素*/
scanf("%d",&y);
Q=enqueue(Q,y);/*调用队列插入函数*/
printf("the queue after insert is:\n");/*提示显示执行入队操作后的队列*/
display(Q);/*调用队列元素输出函数*/
Q=dequeue(Q,&e);/*调用队列删除函数*/
printf("the delete data queue after delete is:\n");/*提示显示执行出队操作后的队列*/
display(Q);/*调用队列元素输出函数*/
}
五、链式队列
链式队列(linked queue)是2018年公布的计算机科学技术名词,采用链式存储结构的队列。
1、运行结果
2、具体代码
# include六、字符串
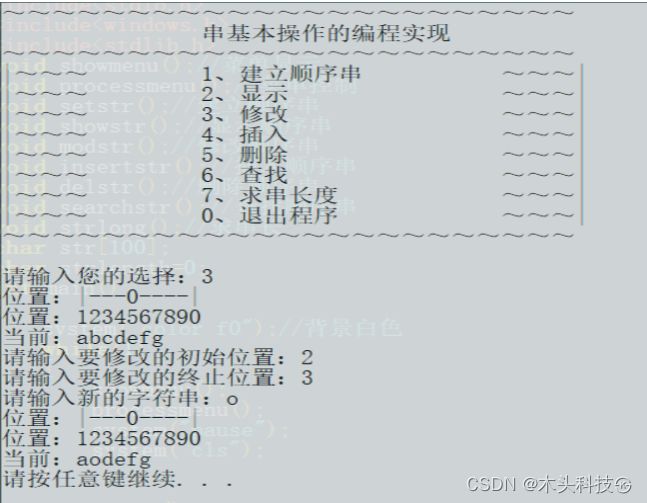
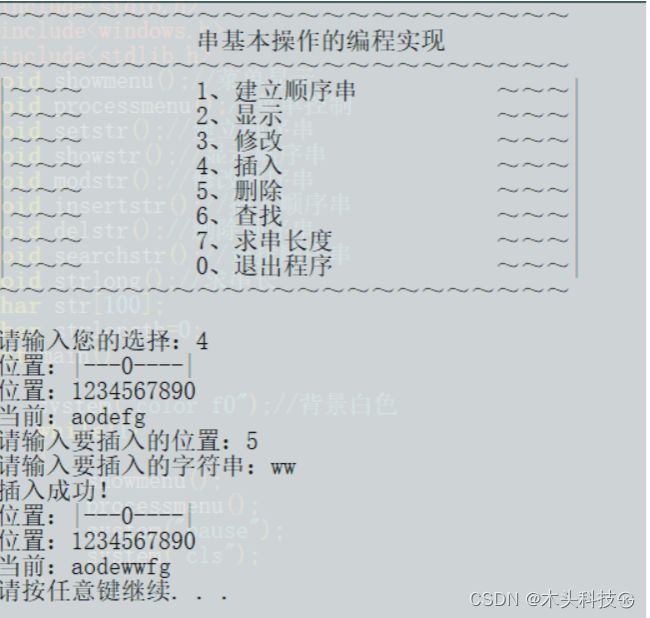
字符串主要用于编程,概念说明、函数解释、用法详述见正文,这里补充一点:字符串在存储上类似字符数组,所以它每一位的单个元素都是可以提取的,如s=“abcdefghij”,则s[1]=“b”,s[9]=“j”,这可以给我们提供很多方便,如高精度运算时每一位都可以转化为数字存入数组。
1、运行结果
2、具体代码
#include<stdio.h>
#include七、二叉树
二叉树(Binary tree)是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式,即使是一般的树也能简单地转换为二叉树,而且二叉树的存储结构及其算法都较为简单,因此二叉树显得特别重要。二叉树特点是每个节点最多只能有两棵子树,且有左右之分。
1、运行结果
2、具体代码
#include