数据分析第五章课后实训--应用Matplotlib、seaborn、pyecharts库可视化分析(答案到任务三)
实验名称 应用Matplotlib、seaborn、pyecharts库可视化分析
实验时间 2023.5.10
一、实验目的
1、掌握 pyplot的基础语法。
2、掌握饼图的绘制方法。
3、掌握箱线图的绘制方法。
4、掌握子图的绘制方法。
5、掌握柱形图的绘制方法。
6、掌握NumPy库中相关函数的使用方法。
7、掌握分类散点图的绘制方法。
8、掌握线性回归拟合图的绘制方法。
9、掌握热力图的绘制方法。
10、掌握漏斗图的绘制方法。
11、掌握词云图的绘制方法。
二、实验仪器设备或材料
笔记本电脑,Anaconda软件
三、实验原理
1、 需求说明
在期末考试后,学校对学生的期末考试成绩及其他特征信息进行了统计、并存为学生成绩特征关系表(student grade.xlsx)。学生成绩特征关系表共有7个特征,分别为性别、午餐、考试课程准备情况、数学成绩、阅读成绩、写作成绩和总成绩,其部分数据如表5-40所示。为了解学生考试总成绩的分布情况,将总成绩按0150、150200、200~250、250~300区间划分为“不及格”“及格”“良好”“优秀”4个等级,通过绘制饼图查看各区间学生人数比例,并通过绘制箱线图查看学生3项单科成绩的分散情况。

2、需求说明
为了了解学生父母教育水平、午餐、考试课程准备情况这两个特征与总式绩之间是否存在某些关系,基于实训1的数据,对这3个特征下不同值所对应的学生总成绩求均值,绘制折线图分别查看父母教育水平与总成绩的关系,绘制柱形图分别查看午餐、考试课程准备情况与总成绩的关系,并对结果进行分析。
的学号、姓名和班级信息。
3、需求说明
空气质量指数(Air Quality Index,AOI)是能够对空气质量进行定量描述的数据。空气质量(Air quality)反映了空气污染程度,它是依据空气中污染物浓度来判断的。空气污染是一个复杂的现象,空气污染物浓度受到许多因素影响。
某市2020年1月—9月AQI的部分数据如表5-41所示。

本实训将基于表5-41所示的数据绘制分类散点图、回归拟合图,分析 PM2.5浓度与AQI的关系,以及AQI的分类情况。同时绘制热力图,分析合空气质量指标与AQI的相关性。
4、需求说明
某商场在不同地点投放了5台自动售货机,编号分别为A、B、C、D、E,同时记录了2017年6月每台自动售货机的商品销售数据。为了了解各商品的销售情况,以二级类别进行分类,统计排名前5的商品类别销售额,并绘制漏斗图,同时根据商品销售数量、商品名称绘制词云图。
四、实验内容与步骤
任务1:分析学生考试成绩特征的分布与分散情况。
1、实现思路与步骤
(1)使用pandas库读取学生考试成绩数据。
(2)将学生考试总成绩分为4个区间,计算各区间下的学生人数,绘制学生考试总成绩分布饼图。
(3)提取学生3项单科成绩的数据,绘制学生各项考试成绩分散情况箱线图。
(4)分析学生考试总成绩的分布情况和3项单科成绩的分散情况。
任务2:分析学生考试成绩与各个特征之间的关系。
2、实现思路与步骤
(1)创建画布,并添加子图。
(2)使用NumPy库中的均值函数求学生父母教育水平、午餐、考试课程情3个特征下对应学生总成绩的平均数。
(3)在子图上绘制对应的折线图或柱形图。
(4)分析3 个特征与考试总成绩的关系。
任务3:分析各空气质量指数之间的相关关系。
3、实现思路与步骤
(1)使用pandas南法晌杖古2020年工日—9月AOI统计数据。
(2)解决中文显示问顺,设置字体为黑体,并解决保存图像时负号“-”显示为方块的问题。
(3)绘制质量等级分类散点图。
(4)绘制PM2.5浓度与AOI线性回归拟合图。
(5)计算相关系数。
(6)绘制空气质量特征相关性热力图。
任务4:绘制交互式基础图形
4、实现思路与步骤
(1)获取商品销售数据。
(2)按照二级类别统计商品类别销售额。
(3)统计商品销售数量。
(4)设置系列配置项和全局配置项,绘制销售额前5的商品类别漏斗图。
(5)设置系列配置项和全局配置项,绘制商品销售数量和商品名称的词云图。
五、实验结果与分析
任务一:
该饼图展示了学生考试总成绩分布情况,分为4个区间。从饼图中可以看出,150-200分区间的学生人数最多,占比为34.3%;可以看出,大部分学生的考试总成绩都在优良以上,说明这个班级整体成绩较好。
箱线图是一种统计图形,可以用来展示一组数据的分布情况。箱线图包含以下内容:
- 上边缘(Max):最大值,即数据中最大的值。
- 下边缘(Min):最小值,即数据中最小的值。
- 中位数(Median):数据的中间值,将数据按照大小排序后,位于中间的值。
- 上四分位数(Q3):将数据分成四等份,上边界那一份的最后一个数据点。
- 下四分位数(Q1):将数据分成四等份,下边界那一份的第一个数据点。
- 内限:上四分位数和下四分位数之间的距离,称为“箱子”。
- 外限:上边缘和下边缘之间的距离,称为“须子”。
箱线图的作用: - 可以直观地展示数据的分布情况,包括数据的极值、中位数和四分位数等统计量,让人能够比较直观地了解数据的情况。
- 可以快速识别和处理离群值,这些离群值可能在某些情况下对数据分析产生极大的影响。
- 可以比较不同组数据的分布情况,在数据分析和决策方面具有重要的作用。
任务二:
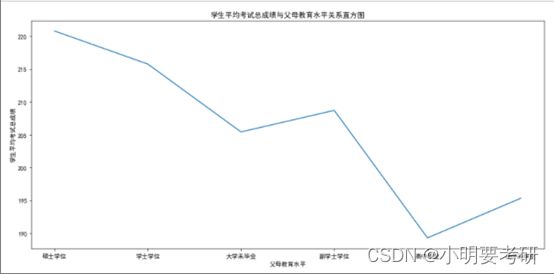
根据折线图,可以看出学生的平均考试总成绩在不同父母教育水平下存在差异。硕士学位的父母的孩子平均考试总成绩最高,为220.8分,而高中未毕业的父母的孩子平均考试总成绩最低,为189.29分。这表明父母的教育水平对孩子的学习成绩有一定的影响。
此外,可以看出学士学位和副学士学位的父母的孩子平均考试总成绩相对较高,而大学未毕业的父母的孩子平均考试总成绩较低。这可能是因为学士学位和副学士学位的父母对孩子的教育有更高的期望和更好的教育资源,而大学未毕业的父母可能无法提供足够的支持和资源。
总之,父母的教育水平对孩子的学习成绩有一定的影响,但并不是唯一的因素,还有其他因素如个人天赋、学习态度等也会影响学习成绩。
任务三:
可以看出空气质量指数(AQI)的值在不同时间点存在差异。其中,最高的AQI值为203,属于重度污染,最低的AQI值为22,属于优良。同时,可以看出AQI值的分布呈现出多数值偏低、少数值偏高的趋势,即大部分时间空气质量较好,但也存在部分时间空气质量较差的情况。
此外,可以看出AQI值与空气质量等级之间存在一定的对应关系。AQI值在0-50之间时,空气质量等级为优;在51-100之间时,空气质量等级为良;在101-150之间时,空气质量等级为轻度污染;在151-200之间时,空气质量等级为中度污染;在201-300之间时,空气质量等级为重度污染。因此,可以根据AQI值来判断当时的空气质量等级。
总之,空气质量指数(AQI)是衡量空气质量的重要指标,其值的变化反映了空气质量的变化情况,对人们的健康和生活产生着重要的影响。
可以看出AQI值与PM2.5含量之间存在一定的对应关系。PM2.5是指空气中直径小于或等于2.5微米的颗粒物,是空气污染的主要成分之一。从数据中可以看出,AQI值和PM2.5含量的值在大部分时间内呈现出一致的变化趋势,即AQI值和PM2.5含量的值都较低或都较高。这表明PM2.5含量是影响AQI值的重要因素之一。
此外,可以看出AQI值和PM2.5含量的值都存在较大的波动,即AQI值和PM2.5含量的值在不同时间点之间存在较大的差异。这可能是由于空气污染源的不同、气象条件的变化等因素导致的。
总之,AQI值和PM2.5含量是反映空气质量的两个重要指标,它们的变化情况反映了空气质量的变化情况,对人们的健康和生活产生着重要的影响。
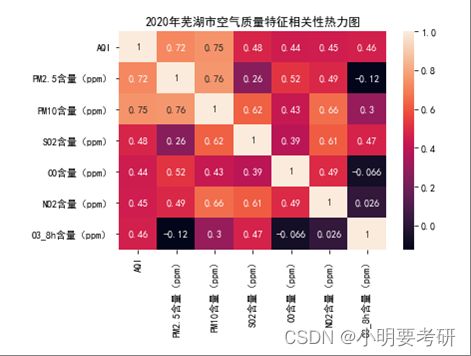
空气质量特征相关性分析可以为我们提供不同污染物指标之间的相互关系,有助于识别主要的污染源和制定特定的环境科学政策。我们可以使用皮尔逊相关系数衡量变量之间的线性关系,取值范围从-1到+1,其中0表示没有线性关系,-1表示完全负相关,+1表示完全正相关。
从上图中可以看出,以下数据是相关联的:
PM2.5含量与PM10含量:相关系数为0.97,两者呈强正相关。
NO2含量与PM2.5含量、PM10含量:相关系数分别为0.79和0.78,NO2含量与PM2.5含量、PM10含量呈正相关。
O3_8h含量与AQI:相关系数为0.6,AQI与O3_8h含量呈正相关。
需要注意的是,相关系数只能反映变量之间的线性关系,而不能表示非线性关系,因此在实际应用中需要综合考虑其他因素。
任务四:
可以看出销量比较好的是:乳制品,饮料,肉干,饼干,功能饮料等,这些商品都是日常生活的必需品,商店可以多售卖此类商品。
上图可看出怡宝纯净水是卖的最好的一个商品,其次是豆奶,热狗肠虾条等。
词云图是一种可视化展示文本数据的图表,其中文本数据中的单词按照频率大小呈现出来,并以不同的字体大小或颜色等形式区分重要程度。通常情况下,词云图被用于处理海量文本数据,可以快速了解文本中的关键信息或主题,并帮助用户快速理解文本中的重点。在情感分析、舆情分析、市场调查和新闻报道等领域广泛应用。
六、结论与体会
matplotlib、seaborn 和 pyecharts 作为可视化分析的常用库,提供了强大、灵活和易用的工具,支持各种图表类型的生成,可以帮助我们更好地理解数据分析结果。
在实际应用中,matplotlib 是最常用的绘图库之一,包含了丰富的数据可视化函数,支持绘制多种类型的图形和自定义样式,因此它可以满足大多数绘图需求。如果需要更高效的绘图和更具读者友好性的可视化,seaborn 就是你的首选。它是 matplotlib 的扩展库,提供了许多高级函数和绘图工具,使得数据分析和可视化更加简单和优雅。对于更加复杂的数据可视化场景,可以考虑使用 pyecharts,它是基于 ECharts 的 Python 可视化库,支持生成动态交互式图表,可以使得数据展示更生动、直观。
总的来说,可视化分析库的选择应该视数据类型和可视化需求而定。在进行数据分析时,用到的图形种类很多,例如条形图、折线图、饼图、散点图、热图等等。要准确刻画数据的特点,并得出有意义的结论和推论,就需要选择正确的可视化工具和图形类型。此外,美观的可视化效果也会让讲述和分享数据分析结果更具吸引力和说服力。所以,熟练使用可视化分析库是提升分析师工作效率和数据分析质量的必备技能。
任务1代码:
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = 'SimHei' # 设置中文显示
plt.rcParams['axes.unicode_minus'] = False
data = np.load(r'./data/student_grade.npz', encoding='ASCII',
allow_pickle=True)
columns = data['arr_0']
values = data['arr_1']
# 定义成绩变量
sum_score = values[:, -1]
math_grade = values[:, -4]
reading_grade = values[:, -3]
writing_grade = values[:, -2]
all_grade = values[:, -1]
student_id = np.arange(len(values))
p = plt.figure(figsize=(15, 15)) # 设置画布
# 提取学生考试总成绩区间人数
grade_0_150 = 0
grade_150_200 = 0
grade_200_250 = 0
grade_250_300 = 0
for i in range(len(values)):
if 0 < values[i, -1] <= 150:
grade_0_150 += 1
elif 150 < values[i, -1] <= 200:
grade_150_200 += 1
elif 200 < values[i, -1] <= 250:
grade_200_250 += 1
elif 250 < values[i, -1] <= 300:
grade_250_300 += 1
all_stu_grade = [grade_0_150, grade_150_200, grade_200_250, grade_250_300]
饼图:
# 绘制学生考试总成绩的总体分布情况饼图
p = plt.figure(figsize=(9, 9)) # 设置画布
label= ['不及格', '及格', '良好', '优秀']
explode = [0.01,0.01,0.01,0.01] # 设定各项离心n个半径
plt.pie(all_stu_grade, explode=explode, labels=label,
autopct='%1.1f%%', textprops={'fontsize': 15}) # 绘制饼图
plt.title('学生考试总成绩的总体分布情况饼图', fontsize=20)
plt.savefig('./tmp/学生考试总成绩的总体分布情况饼图.png')
plt.show()
#箱线图
# 绘制学生考试总成绩的总体分散情况箱线图
p = plt.figure(figsize=(12, 8))
label= ['总成绩']
gdp = (list(sum_score))
plt.boxplot(gdp,notch=True,labels=label, meanline=True) # 绘制箱线图
plt.xlabel('学生考试科目')
plt.ylabel('学生考试总分数')
plt.title('学生考试总成绩的总体分散情况箱线图', fontsize=20)
plt.savefig('./tmp/学生考试总成绩的总体分散情况箱线图.png')
plt.show()
# 绘制学生考试总成绩的总体分散情况箱线图
p = plt.figure(figsize=(12, 8))
label= ['数学成绩','阅读成绩','写作成绩']
gdp = (list(math_grade), list(reading_grade), list(writing_grade))
plt.boxplot(gdp,notch=True,labels=label, meanline=True) # 绘制箱线图
plt.xlabel('学生考试科目')
plt.ylabel('学生考试分数')
plt.title('学生各项考试成绩的总体分散情况箱线图', fontsize=20)
plt.savefig('./tmp/学生各项考试成绩的总体分散情况箱线图.png')
plt.show()
#任务二
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = 'SimHei' # 设置中文显示
plt.rcParams['axes.unicode_minus'] = False
data = np.load(r'./data/student_grade.npz', encoding='ASCII', allow_pickle=True)
columns = data['arr_0']
values = data['arr_1']
# 分别提取学生父母教育水平对应的总成绩
master = []
bachelor = []
undergraduate_college = []
associate = []
highschool = []
undergraduate_highschool = []
all_grade = values[:, -1]
for i in range(len(values)):
if values[i, 2] == '硕士学位':
master.append(values[i, -1])
elif values[i, 2] == '学士学位':
bachelor.append(values[i, -1])
elif values[i, 2] == '大学未毕业':
undergraduate_college.append(values[i, -1])
elif values[i, 2] == '副学士学位':
associate.append(values[i, -1])
elif values[i, 2] == '高中毕业':
highschool.append(values[i, -1])
elif values[i, 2] == '高中未毕业':
undergraduate_highschool.append(values[i, -1])
# 分别计算学生父母教育水平对应的总成绩均值
mean_master = round(np.mean(master), 2) #round保留两位小数
mean_bachelor = round(np.mean(bachelor), 2)
mean_undergraduate_college = round(np.mean(undergraduate_college), 2)
mean_associate = round(np.mean(associate), 2)
mean_highschool = round(np.mean(highschool), 2)
mean_undergraduate_highschool = round(np.mean(undergraduate_highschool), 2)
#把平均值加到列表里
mean_education_grade = [mean_master, mean_bachelor,
mean_undergraduate_college, mean_associate,
mean_highschool, mean_undergraduate_highschool]
# 分别提取学生午餐情况对应的总成绩
standard = []
reduced = []
all_grade = values[:, -1]
for i in range(len(values)):
if values[i,3] == '标准':
standard.append(values[i, -1])
else:
reduced.append(values[i, -1])
# 分别计算学生午餐情况对应的总成绩均值
mean_standard = round(np.mean(standard), 2)
mean_reduced = round(np.mean(reduced), 2)
mean_lunch_grade = [mean_standard, mean_reduced]
# 分别提取学生考试准备情况对应的总成绩
completed = []
uncompleted = []
all_grade = values[:, -1]
for i in range(len(values)):
if values[i, 4] == '完成':
completed.append(values[i, -1])
else:
uncompleted.append(values[i, -1])
# 分别计算学生完成考试准备和未完成考试准备对应的总成绩均值
mean_completed = round(np.mean(completed), 2)
mean_uncompleted = round(np.mean(uncompleted), 2)
mean_prepartion_grade = [mean_completed, mean_uncompleted]
# print(mean_prepartion_grade)
p = plt.figure(figsize=(13, 13)) #设置画布
# 子图1
ax1 = p.add_subplot(2, 1, 1)
label = ['硕士学位', '学士学位', '大学未毕业', '副学士学位', '高中毕业', '高中未毕业']
plt.plot(range(6), mean_education_grade) # 绘制折线图
plt.xlabel('父母教育水平')
plt.ylabel('学生平均考试总成绩')
plt.xticks(range(6), label)
plt.title('学生平均考试总成绩与父母教育水平关系直方图')
# 子图2
ax2 = p.add_subplot(2, 2, 3)
label = ['标准', '免费/简单']
plt.bar(range(2), mean_lunch_grade, width=0.4) # 绘制直方图
plt.xlabel('午餐情况')
plt.ylabel('学生平均考试总成绩')
plt.xticks(range(2), label)
plt.title('学生平均考试总成绩与午餐情况关系直方图')
# 子图3
ax2 = p.add_subplot(2, 2, 4)
label = ['已完成', '未完成']
plt.bar(range(2), mean_prepartion_grade, width=0.4) # 绘制直方图
plt.xlabel('考试课程准备情况')
plt.ylabel('学生平均考试总成绩')
plt.xticks(range(2), label)
plt.title('学生平均考试总成绩与考试课程准备情况关系直方图')
plt.savefig('./tmp/学生考试总成绩与各个特征关系图.png')
plt.show()
#任务三
import matplotlib.pyplot as plt
import pandas as pd
# 设置中文字体
plt.rcParams['font.sans-serif'] = ['SimHei'] # 解决中文显示问题-设置字体为黑体
plt.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题
# 忽略警告
import warnings
warnings.filterwarnings('ignore')
import seaborn as sns
# 读取数据
data = pd.read_csv('./data/aqi.csv')
# --------------------绘制空气质量等级分类图--------------------
with sns.axes_style('whitegrid'):
sns.stripplot(x=data['质量等级'])
ax = sns.stripplot(x='质量等级', y='AQI', data=data, jitter=True)
ax.set_title('2020年芜湖市空气质量等级分类图')
plt.show()
# --------------------绘制AQI与PM2.5线性回归拟合图--------------------
ax = sns.regplot(x='PM2.5含量(ppm)', y='AQI', data=data)
ax.set_title('2020年芜湖市空气质量指数PM2.5与AQI回归拟合图')
plt.show()
# 计算相关系数
corr_data = data.corr()
# --------------------绘制特征相关性热力图--------------------
ax = sns.heatmap(corr_data, annot=True)
ax.set_title('2020年芜湖市空气质量特征相关性热力图')
plt.show()