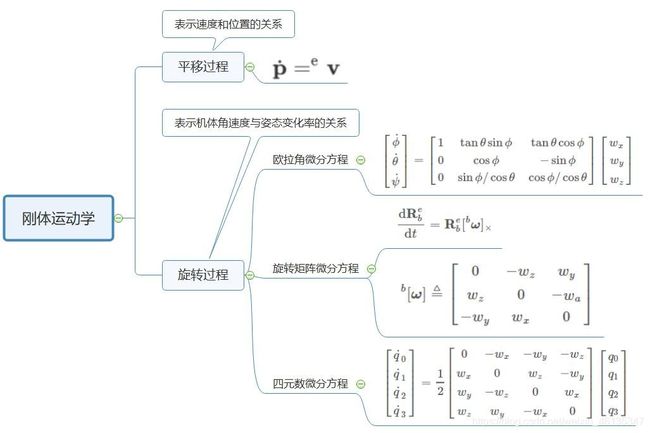
【SLAM学习笔记1】欧拉角之万向锁问题（Gimbal Lock）

---

前言

之前看视觉SLAM14讲时，看到欧拉角的万向锁问题，当时没搞懂，这两天突然又看到这个问题，看了很多帖子和动画，其实大家讲得都不清不楚，很多人没讲明白为什么会有坐标轴平行的情况，我在此尝试把自己理解的记录下来，有什么不妥之处，请多指教。

---

一、欧拉角

1.欧拉角是什么？

对于物体旋转这件事，研究人员慢慢定义和形成了很多种表达方式，其中欧拉角便是其中之一。
欧拉角直观地将旋转描述成3次旋转，其分解旋转的方式有很多种，所以欧拉角存在着许多种定义方式，最常见的是ZYX，当然也可以定义XYZ、ZYZ等旋转方式。即：
物体的任何一种旋转都可分解为分别绕三个轴的旋转，但分解方式不唯一。

如果继续划分，还可以按是否绕固定轴旋转分为动态欧拉角和静态欧拉角：

静态欧拉角：其旋转的旋转轴为静止不动的世界坐标系的坐标轴（笛卡尔坐标系），故称为静态欧拉角。
动态欧拉角：在刚体上建立的坐标系，因而坐标系会随着刚体的旋转而旋转，称其为物体坐标系，所有旋转围绕动态的物体坐标轴进行，故称为动态欧拉角。
在运用上，静态欧拉角相对于动态欧拉角更有意义。

2.使用欧拉角的优缺点

优点：
① 使用便利，可依据需要定义不同的欧拉角；
② 相对于旋转矩阵而言，表达简洁；
③ 任意三个角都是合法的。

缺点：
① 给定方位的表达方式不唯一；
② 两个角度间求插值非常困难。

---

二、万向锁问题的预备知识

1.Gimbal（平衡架）

平衡架（Gimbal）是一个枢转支撑，其允许围绕轴线的对象的旋转。一组三个万向架，一个以正交的枢轴安装在另一个上，可以用来允许安装在最里面的万向架上的物体保持独立于其支撑的旋转。
例如，在船上，陀螺仪，船上指南针，火炉甚至饮料架通常都使用万向架使它们相对于地平线保持直立，即使船在俯仰和滚动时也是如此（维基百科）

2.相关术语

在飞行器的航行中，进行XYZ三个方向旋转的旋转有专业的术语roll-pitch-yaw，如图所示：

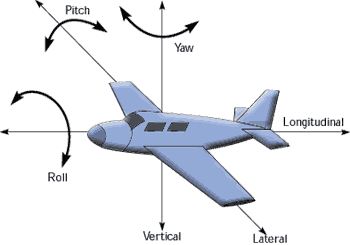
沿着机身右方轴（欧拉角向量的X轴）进行旋转，称为Pitch，中文叫俯仰。
沿着机头上方轴（欧拉角向量的Y轴）进行旋转，称为Yaw，中文叫偏航。
沿着机头前方轴（欧拉角向量的Z轴）进行旋转，称为Roll，中文叫桶滚。

对应着的还有另一组术语，叫heading-pitch-bank，其中的roll对应与bank，yaw对应于heading，它定义了从物体坐标系到惯性坐标系的旋转顺序，其中先heading45°再pitch90°等价于先pitch90°再bank45°（涉及死锁问题）。

注：惯性坐标系：与物体坐标系原点相同，其坐标轴的方向与世界坐标系相同，作用是物体坐标系与世界坐标系变换的媒介，或者叫过渡吧。

三、万向锁问题

1.Gimbal Lock（万向锁问题）的现象

Gimbal Lock，顾名思义一开始是平衡环之间锁死问题，其实也不是锁死，只是当Pitch = ±90°时，绕第三个轴旋转的欧拉角和绕第一个轴旋转的欧拉角效果相同，即系统失去了一个自由度，出现了奇异性。

听我娓娓道来：

用三种颜色定义平衡环的三个环，RGB分别代表坐标系的XYZ轴，平衡环之间会有一个父子关系（这个关系犹如SolidWorks建模的父子关系和C++继承里的父子关系），最先运动的环会带动另外两个环运动，即绕某一轴旋转会改变另外两轴的方向，第二个运动的环会带动下一级环运动，即假设旋转顺序是YXZ，旋转y轴x和z轴都变，旋转x轴只有z轴变化，旋转z轴其它轴不变。。

视频里定义欧拉角的顺序是：YXZ，初始状态如下图所示：

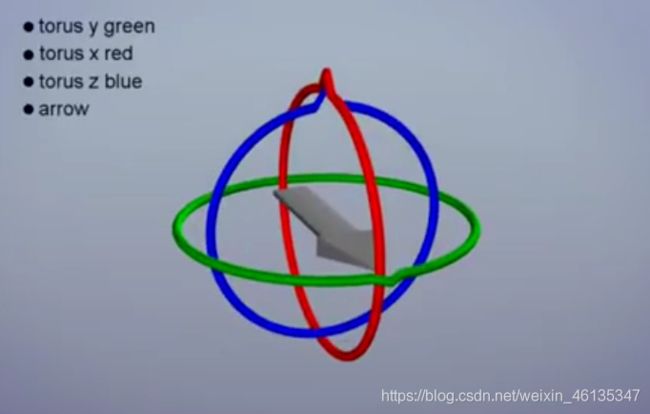
随后开始进行旋转，首先是Y轴，Y轴随便转都不会出现什么问题；其次是绕X轴旋转，正常旋转（Pitch≠±90°）是这样的：

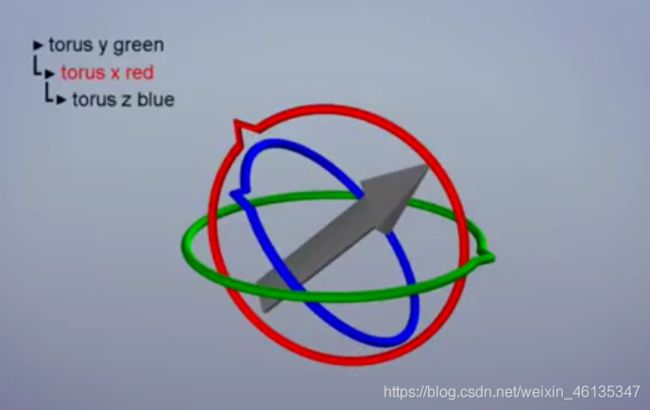
当绕X轴旋转90°时，就会出现两个环平行（如下图所示），接着旋转第三个环，即绕Z轴旋转时，就会产生与第一次旋转（绕Y轴旋转）一样的效果，此时丧失了一个方向的自由度，即出现了奇异性。这便是“Gimbal Lock（万向锁问题）”。

一共有6种情况会产生这种现象，即三个旋转分别围绕XYZ三轴旋转进行，就会产生万向锁现象。

每种情况在第二个旋转时，就会发生万向锁现象。

2.Gimbal Lock（万向锁问题）出现的原因

从物体的空间旋转角度解释：

很多人应该会有疑问：
为什么明明旋转的时候都是一起在旋转，怎么可能会出现两轴平行的情况？
旋转到底是在哪个坐标系上旋转的？

个人认为，万向锁问题最为严谨的说法是@高翔在书里说的：

万向锁问题会导致第三次旋转和第一次旋转的效果相同。

如果非要跟两轴位置扯上关系，就会出现上述的两个问题。好在问题终究是有答案的。

在@创世界— dalao的博文和实践动图中可以得出结论：

假设还是YXZ的旋转顺序，绕y轴的旋转将影响x和z轴，绕y轴的旋转变换是物体在惯性坐标系下的变换，而绕其他轴的旋转变换是在物体坐标系下的变换，当绕x轴旋转90°时，接下来绕z轴旋转，就会产生旋转y轴（惯性坐标系）和旋转z轴（物体坐标系）是一样的效果，只不过方向相反或相同，即万向锁问题。

上述解释其实跟视频里的又有点不一样，视频中所有的旋转都是围绕惯性坐标系旋转，但是还是会出现万向锁问题，归根结底如下：

最终结论：

1、万向锁产生时，两个旋转轴平行（旋转面共面）使模型的旋转失去的一个方向的旋转。

2、最主要的是弄明白旋转是围绕着哪个坐标系做旋转。

3、万向锁问题是其本身定义上的不足而产生的！任意旋转分别绕x,y,z三个轴旋转合成都会造成万向锁问题！

从数学的角度解析：

由上式可知：

只有欧拉角微分方程里，cos pitch 不能为0 ，即pitch≠±90°。

那么，当pitch=±90°，便会产生万向锁问题。

为什么只有欧拉角有死锁问题？

因为只有欧拉角(zyx顺序)描述旋转运动时，其方程中存在约束，pitch不能为±90°，而旋转矩阵微分方程，和四元数微分方程则不存在约束，他们的方程中的元素都是角速度，角速度可以随意选取，方程依然有效。

三种表达各自的特点：

① 欧拉角最直观、最容易理解、存储空间少，但是欧拉角存在万向锁现象、插值速度不均匀等缺点，而且不可以在计算机中直接运算；

② 四元素不存在万向锁问题、利用球面插值可以获得均匀的转速、存储空间也较少，但是不好理解、不直观；

③ 旋转矩阵法是最便于计算机处理的，但不可以直接插值、冗余信息多、费存储空间，同样不直观。

所以，在机器人学中，一般人机交互端会用欧拉角，插值等用四元数，正逆运动学运算中用矩阵表示法。

3.如何避免万向锁问题？

① heading取值范围在（-pi,+pi），pitch取值范围为（-pi/2,+pi/2），或者直接这么理解：尽量将你所设计的物体Pitch置于不需要旋转到pi/2的方向上；

② 在SLAM中尽量不适用欧拉角进行姿态和旋转的表达。

---

四、Reference

博文：
https://blog.csdn.net/fengya1/article/details/50721768
https://blog.csdn.net/icevmj/article/details/80280929
https://blog.csdn.net/caimouse/article/details/55259669
https://blog.csdn.net/weixin_39904268/article/details/112417665

视频：
https://www.bilibili.com/video/BV1YJ41127qe?from=search&seid=9449299655882540853

图源：
上述博文、视频截图及wiki百科。