网络流之最大流算法总结(FF, EK, Dinic)
目录
FF算法:最基础的最大流算法
EK算法:每次BFS寻找増广路
Dinic算法:EK算法的优化
Dinic+链式前向星
这里以POJ1273这道题为例,题目链接:http://poj.org/problem?id=1273
FF算法:最基础的最大流算法
通过DFS増广,直到不能増广为止。
记最大流的流量为F,FF算法最多进行F次DFS,所以其复杂度为O(F|E|),每一次DFS的复杂度不确定,但是最坏的情况几乎是不存在的,所以还是比较快的。
最大流算法的精髓就是加了一条反向边,给了程序有一个后悔的机会,在一次DFS结束之后,每条正向边减去流向汇点的流量,每条反向边加上流向汇点的流量。
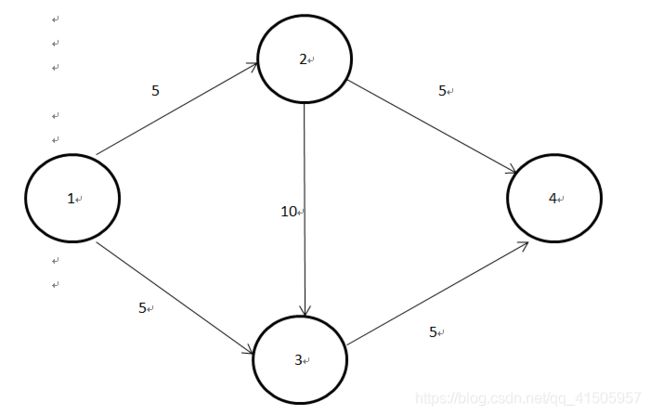
以下面这个图为例,第一次寻找的増广路是1->2->3->4,流量是5,如果没有反向边的话,就已经不能再増广了,但是很明显这不是最佳策略。
在引入反向边后可以发现,有一条新的増广路1->3->2->4,流量为5,最后发现没有増广了,求得最大流为10。
在FF算法中边是用邻接表来存储的,但是每次正向边和反向边的加减是要同时进行,所以在知道正向边的同时,要知道反向边的位置,所以结构体中有一个rev来存储反向边的位置。
#include
#include
#include
#include
#define N 10020
using namespace std;
int n, m, inf=0x7f7f7f;
bool book[N];
struct edge {
int v;
int w;
int rev; //在反向边中存储的位置
};
vectore[N];
void add(int u, int v, int w) //加边
{
e[u].push_back(edge{ v, w, e[v].size() });
e[v].push_back(edge{ u, 0, e[u].size() - 1 });
}
int dfs(int s, int t, int f)
{
if (s == t)
return f; //找到终点
book[s] = true;
for (int i = 0; i < e[s].size(); i++)
{
edge &G = e[s][i];
if (G.w > 0 && book[G.v] == false)
{
int d = dfs(G.v, t, min(f, G.w)); //两者之间流量较小的一个
if (d > 0)
{
G.w -= d; //改变正向边和反向边
e[G.v][G.rev].w += d;
return d;
}
}
}
return 0;
}
int FF(int s, int t)
{
int ans = 0;
while (1)
{
memset(book, false, sizeof(book)); //每次找増广路
int d = dfs(s, t, inf);
if (d == 0) //找不到增广路返回总流量
return ans;
ans += d;
}
}
int main()
{
int u, v, w;
while (scanf("%d%d", &m, &n) != EOF)
{
for (int i = 1; i <= n; i++)
e[i].clear();
for (int i = 0; i < m; i++)
{
scanf("%d%d%d", &u, &v, &w);
add(u, v, w);
}
printf("%d\n", FF(1, n));
}
return 0;
} ![]()
EK算法:每次BFS寻找増广路
EK算法是基于FF算法的,只是边的存储变为邻接矩阵存储,求増广路的过程变为BFS,在正向边和反向边的改变上也有变化,但是总体上的思路是一样的,或者说FF, EK, Dinic这三者的思想是相同的。
EK算法的时间复杂度是O(V*E^2)适合边较少的稀疏图。
因为EK算法图的存储是用邻接矩阵存储,所以每次在输入流量的时候应该加上原有的流量,在这道题上也有体现。
因为EK算法不能像FF算法中递归改变边的流量,所以在EK算法中记录的每一个点的匹配点,通过匹配点来改变边的流量,这一点只要仔细想想应该能明白。
#include
#include
#include
#include
#define N 220
using namespace std;
int n, m, e[N][N], pre[N], flow[N], inf=0x7f7f7f;
int bfs(int s, int t)
{
memset(pre, -1, sizeof(pre));
queueq;
q.push(s);
flow[s] = inf; //最开始流量为无穷
while (!q.empty())
{
int u = q.front();
q.pop();
for (int v = 1; v <= n; v++) //求増广路
{
if (e[u][v] > 0 && v != s && pre[v] == -1) //注意v!=s
{
pre[v] = u;
q.push(v);
flow[v] = min(flow[u], e[u][v]); //现在的流量是流过来的流量和可以流走的量的最小值
}
}
}
if (pre[t] == -1) //如果没有到达终点
return -1;
return flow[t]; //返回流量
}
int EK(int s, int t)
{
int ans = 0;
while (1)
{
int d = bfs(s, t);
if (d == -1) //无法在找増广路
break;
ans += d;
int p = t;
while (p != s) //边的流量发生改变
{
e[pre[p]][p] -= d;
e[p][pre[p]] += d;
p = pre[p];
}
}
return ans;
}
int main()
{
int u, v, w;
while (scanf("%d%d", &m, &n) != EOF)
{
memset(e, 0, sizeof(e));
while (m--)
{
scanf("%d%d%d", &u, &v, &w);
e[u][v] += w; //这里要加上原有的流量
}
printf("%d\n", EK(1, n));
}
return 0;
} ![]()
Dinic算法:EK算法的优化
Dinic算法是EK算法的优化,实际上和FF算法也是很像的, Dinic通过BFS分层,在用DFS求増广路,可以达到多路増广的效果,基本上Dinic算法是比较优秀的算法了。
众所周知,网络流题目会卡FF和EK,但是不会卡Dinic[笑]。
可以看到加边操作是和FF算法是一样的,分层也是一个比较常规的操作。
Dinic算法引入了一个当前弧优化:在一次BFS分层中已经搜索过的边不用再搜。
#include
#include
#include
#include
#include
#define N 220
using namespace std;
struct edge {
int v;
int w;
int rev;
};
vectore[N];
int n, m, inf=99999999, dis[N], iter[N];
bool book[N];
void add(int u, int v, int w) //加边
{
e[u].push_back(edge{ v, w, e[v].size() });
e[v].push_back(edge{ u, 0, e[u].size() - 1 });
}
void bfs(int s) //分层
{
queue q;
memset(dis, -1, sizeof(dis));
dis[s] = 0;
q.push(s);
while (!q.empty())
{
int u = q.front();
q.pop();
for (int v = 0; v < e[u].size(); v++)
{
edge G = e[u][v];
if (dis[G.v] == -1 && G.w) //有流量时才加入
{
dis[G.v] = dis[u] + 1;
q.push(G.v);
}
}
}
}
int dfs(int s, int t, int f)
{
if (s == t)
return f;
for (int &v = iter[s]; v < e[s].size(); v++) //当前弧优化
{
edge &G = e[s][v];
if (dis[G.v] == dis[s] + 1 && G.w) //只有层数是+1时才増广
{
int d = dfs(G.v, t, min(G.w, f));
if (d > 0)
{
G.w -= d;
e[G.v][G.rev].w += d;
return d;
}
}
}
return 0;
}
int Dinic(int s, int t)
{
int ans = 0;
while (1)
{
bfs(s);
if (dis[t] == -1)
return ans;
int d;
memset(iter, 0, sizeof(iter));
while ((d = dfs(s, t, inf)) > 0) //多次dfs
ans += d;
}
return ans;
}
int main()
{
int u, v, w;
while (scanf("%d%d", &m, &n) != EOF)
{
for (int i = 1; i <= n; i++) //初始化
e[i].clear();
while (m--)
{
scanf("%d%d%d", &u, &v, &w);
add(u, v, w);
}
printf("%d\n", Dinic(1, n));
}
return 0;
} ![]()
下面是把 if (dis[G.v] == dis[s] + 1 && G.w)
改为 if (dis[G.v] > dis[s] && G.w) 的结果
![]()
Dinic+链式前向星
与之前存边的方式有所不同, 这种存边是用链式前向星来存图的。
据说这是当前网络流的主流写法。
有时候不用前向星的话,可能会被卡掉,在hdu4292上有所体现。
这种存图的巧妙之处是把正向边和反向边一起存储,这样正向边=反向边^1(异或1),反向边=正向边^1。
可以看到除了存边不同之外,其他的代码几乎一致。
#include
#include
#include
#include
#define N 220
using namespace std;
struct date {
int v;
int w;
int next;
}edge[N*N];
int n, m, cnt, inf=0x3f3f3f, head[N], dis[N], iter[N];
int add(int u, int v, int w)
{
edge[cnt].v = v; edge[cnt].w = w;
edge[cnt].next = head[u]; head[u] = cnt++;
edge[cnt].v = u; edge[cnt].w = 0;
edge[cnt].next = head[v]; head[v] = cnt++;
}
void bfs(int s)
{
memset(dis, -1, sizeof(dis));
queueq;
q.push(s);
dis[s] = 0;
while (!q.empty())
{
int u = q.front();
q.pop();
for (int v = head[u]; v != -1; v = edge[v].next)
{
date G = edge[v];
if (dis[G.v] == -1 && G.w && G.v != s)
{
dis[G.v] = dis[u] + 1;
q.push(G.v);
}
}
}
}
int dfs(int s, int t, int f)
{
if (s == t)
return f;
for (int &v = iter[s]; v != -1; v = edge[v].next)
{
date &G = edge[v];
if (G.w && dis[G.v] == dis[s] + 1)
{
int d = dfs(G.v, t, min(G.w, f));
if (d > 0)
{
edge[v].w -= d;
edge[v ^ 1].w += d;
return d;
}
}
}
return 0;
}
int Dinic(int s, int t)
{
int ans = 0;
while (1)
{
bfs(s);
if (dis[t] == -1)
return ans;
for (int i = 1; i <= n; i++)
iter[i] = head[i];
int d;
while ((d = dfs(s, t, inf)) > 0)
ans += d;
}
}
int main()
{
int u, v, w;
while (scanf("%d%d", &m, &n) != EOF)
{
cnt = 0;
memset(head, -1, sizeof(head));
while (m--)
{
scanf("%d%d%d", &u, &v, &w);
add(u, v, w);
}
printf("%d\n", Dinic(1, n));
}
return 0;
} ![]()
以上就是几种常见的最大流算法,这几种算法都属于増广路算法,也就是不断求增广路来更新最大流,关于最大流的算法还有很多,可以根据图的不同选取想要的算法。