【数据结构】C语言学习二叉树(下)

❤️前言

        大家好！今天这篇文章我们将一起学习在C语言阶段二叉树知识的下半部分内容，包括二叉树的链式存储，二叉树的前序、中序、后序遍历和层序遍历以及二叉树的创建和销毁。

正文

    1.二叉树的链式存储

        二叉树的链式存储是指用链表的方式来存储一棵二叉树，以链表元素之间的联系来表现二叉树节点之间的关系。二叉树的链式结构又分为二叉链和三叉链，下面是二叉链和三叉链元素的定义。

typedef int BTDataType;
// 二叉链
struct BinaryTreeNode
{
    struct BinTreeNode* pLeft; // 指向当前节点左孩子
    struct BinTreeNode* pRight; // 指向当前节点右孩子
    BTDataType data; // 当前节点值域
}

// 三叉链
struct BinaryTreeNode
{
    struct BinTreeNode* pParent; // 指向当前节点的双亲
    struct BinTreeNode* pLeft; // 指向当前节点左孩子
    struct BinTreeNode* pRight; // 指向当前节点右孩子
    BTDataType data; // 当前节点值域
}；

        当前C语言的学习中，我们更多使用二叉链的链式结构，也就是每个节点包含数据域和左右指针域，左右指针表示指向该节点的左右孩子节点的指针。

        我们在刚开始学习二叉树时，需要一颗二叉树来让我们进行研究，但是我们对于二叉树链式结构的了解还不够深，所以我在这里先手动创建一颗二叉树，以便于我们开始了解二叉树。

typedef int BTDatatype;

typedef struct BinaryTreeNode
{
    BTDatatype data;
    struct BinaryTreeNode* left;
    struct BinaryTreeNode* right;
}BTNode;

//生成二叉树节点
BTNode* BuyBTNode(BTDatatype x)
{
    BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
    if (!newnode)
    {
        perror("malloc fail");
        return NULL;
    }
    newnode->data = x;
    newnode->left = NULL;
    newnode->right = NULL;
    return newnode;
}

//创建一颗二叉树，并手动连接节点
//之后我们便可以在这个函数中进行一些操作
void Test1()
{
    BTNode* node1 = BuyBTNode(1);
    BTNode* node2 = BuyBTNode(2);
    BTNode* node3 = BuyBTNode(3);
    BTNode* node4 = BuyBTNode(4);
    BTNode* node5 = BuyBTNode(5);
    BTNode* node6 = BuyBTNode(6);
    BTNode* node7 = BuyBTNode(7);
    BTNode* node8 = BuyBTNode(8);

    node1->left = node2;
    node1->right = node3;
    node2->left = node4;
    node2->right = node5;
    node3->left = node6;
    node3->right = node7;
    node4->left = node8;
}

    2.二叉树的遍历

        二叉树的遍历有四种形式，分别是前序遍历，中序遍历、后序遍历和层序遍历。前三种遍历方式中的前中后指的是遍历时我们访问节点值的时机：

• 前序遍历中，我们先访问当前节点，然后再访问左孩子，最后访问右孩子。
• 中序遍历中，我们先访问左孩子，然后再访问当前节点，最后访问右孩子。
• 后序遍历中，我们先访问左孩子，然后再访问右孩子，最后访问当前节点。

        与这三者不太相同的层序遍历指的是将二叉树以高度分为不同层数，然后从上到下，从左到右进行访问。

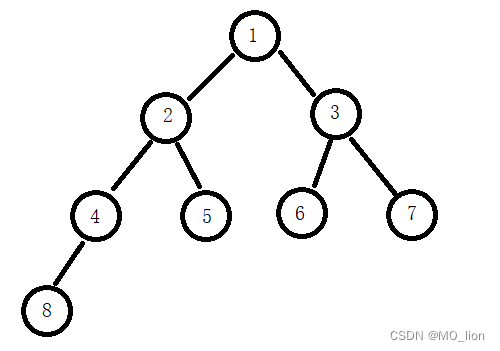
        这里我以上面建立的二叉树模型给出前序遍历的分析思路和代码：

         前序遍历的访问顺序是：节点、左孩子、右孩子，那么我们先访问根节点1，然后访问它的左子树，这时2就成了子树的根节点，那么就访问2，然后接着这个过程分别访问4、8，访问到8时，8的左子树和右子树都为空树，那么就返回到4对右子树的访问，4的右子树也为空树，那么继续返回至2的右子树，2的右子树以5为根节点，即访问5，接着5的左右子树都为空树，返回至2、此时根节点1的左子树就访问完毕，右子树按照相同的规则进行访问，分别按顺序访问了3、6、7这三个节点，也就是说这颗二叉树的前序遍历为12485367，更还原访问顺序的写法是1 2 4 8 NULL NULL NULL 5 NULL NULL 3 6 NULL NULL 7 NULL NULL。

// 二叉树前序遍历 
void BinaryTreePrevOrder(BTNode* root)
{
    if (!root)
    {
        printf("NULL ");
        return;
    }
    printf("%d ", root->data);
    BinaryTreePrevOrder(root->left);
    BinaryTreePrevOrder(root->right);
}

        中序遍历和后序遍历的代码和前序遍历的代码相差不大，大家可以自行编写。

        那么现在根据这个二叉树来了解层序遍历的过程，按照层序遍历的规律，我们对这个二叉树的访问顺序应该是12345678，可以看作是先访问亲代后访问子代的过程，那么我们便可以利用之前学习的队列来进行对二叉树的层序遍历，先让亲代节点的指针进入队列，然后在此节点出队列的同时让它的子代节点指针进入队列，最后队列为空时则层序遍历完成。

// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
    if (!root) return;
    Queue que;
    QueueInit(&que);
    QueuePush(&que, root);
    while (!QueueEmpty(&que))
    {
        BTNode* front = QueuePop(&que);
        printf("%d ", front->data);
        if(front->left) QueuePush(&que,front->left);
        if(front->right) QueuePush(&que, front->right);
    }
    printf("\n");
    QueueDestroy(&que);
}

        这里在层序遍历二叉树时，我没有让空节点进入队列，当然你也可以让空节点也进入队列，当空节点出队列时就打印NULL，并且直接进入下一次的元素出队列。

    3.二叉树的创建与销毁

        我们在创建二叉树时需要知道这个二叉树的节点关系和节点的数据，那么这里就以一道题目作为例子来讲解二叉树的创建和销毁。二叉树遍历_牛客题霸_牛客网 (nowcoder.com)

         题目中我们已经知道了此二叉树的前序遍历(先序遍历)顺序和空树的位置，那么我们便可以以此来创建二叉树，前序遍历的访问顺序是根节点、左子树、右子树，那么我们根据前序遍历创建二叉树时便也是按照根节点，左孩子节点，右孩子节点的顺序进行赋值，而最后的二叉树销毁则是类似于二叉树的后序遍历。

#include 

typedef char BTDatatype;
typedef struct BinaryTreeNode
{
    BTDatatype data;
    struct BinaryTreeNode* left;
    struct BinaryTreeNode* right;
}BTNode;
//根据字符串进行二叉树的创建
BTNode* Createtree(char* a, int* i)
{
    if(a[(*i)] == '#')
    {
        (*i)++;
        return NULL;
    }
    BTNode* root = (BTNode*)malloc(sizeof(BTNode));
    root->data = a[(*i)++];
    root->left = Createtree(a,i);
    root->right = Createtree(a,i);
    return root;
}
//中序遍历
void InOrder(BTNode* tree)
{
    if(!tree) return;
    InOrder(tree->left);
    printf("%c ", tree->data);
    InOrder(tree->right);
}
//二叉树销毁
void TreeDestroy(BTNode* root)
{
    if (root == NULL)
        return;
    TreeDestroy(root->left);
    TreeDestroy(root->right);
    free(root);
}

int main() {
    char in[100];
    scanf("%s", in);
    int i = 0;
    BTNode* tree = Createtree(in,&i);
    InOrder(tree);
    TreeDestroy(tree);
    return 0;
}

结语

        经过这篇文章的学习，在C语言阶段我们对二叉树的讨论就先到此为止啦，期待与大家的下次相见！