机器学习KNN算法原理和应用分析

KNN原理解析

K邻近算法(KNN)，是一种非常简单有效的机器学习算法。KNN是通过计算不同特征值距离作为分类依据，即计算一个待分类对象不同特征值与样本库中每一个样本上对应特征值的差值，将每个维度差值求和也就得到了该组数据与样本之间的距离，一般使用欧式距离进行计算，通过对所有样本求距离，最终得到离待分类对象最近的K个样本，将这K个点作为分类依据。

KNN算法是直接对每个样本进行距离计算，因此要求每个特征必须为数值型数据。由于没有训练过程，KNN也是一种弱训练的机器学习算法，只要我们准备足够多的的样本就可以进行分类。但是带来的问题则是随着样本数量增加，计算所消耗的时间和空间也会不断增加。

假设样本和待分类对象为空间中的一些点，如果特征有n个维度，那么待分类点P(x,y,z...n)与样本点距离可以通过欧式距离公式计算得到。

欧式距离：L=sqrt((x - x1)^2 + (y - y1)^2 + (z - z1)^2+ ...)

另外，为了消除不同特征数值差异造成的权重失衡，需要对每种特征进行内部归一化，假设x的取值范围为1-10，而y的取值范围为100-10000，那么y的变化会对距离计算产生巨大影响，减弱了x的值对距离计算的作用。归一化就是在x和y以及其他维度，将每个维度上的所有值除以该维度内最大值。

K是KNN中唯一的超参数，K的取值可以通过多次测试进行调优。

当K=1时，也就是取离待分类对象距离最近的样本所在类作为分类结果，；

当K>1时，一种方法是计算K个对象中占比最大的类别作为分类结果，另一种方法是采用距离对每种类别占比进行加权，消除粗差。

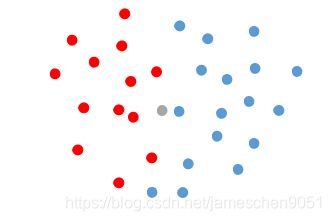
如图：

我们把红色点分为A类，蓝色点分为B类，灰色点作为待分类对象。从距离上看，灰色点距离蓝色点最近，然而有更多的红色点比较靠近灰色点，也就是当K=1时，分类可能出错，因此K的取值对分类结果准确性有比较大的影响。

KNN应用分析

假设我们需要对麻雀，鸽子，老鹰三种鸟成年个体进行分类。由于三种鸟具有明显不同的外形特征，那么可以选择外形作为特征，外形特征则可以选取翼展、体重、身高三个维度生成样本数据。

一组假设的样本数据：

归一化以后：

假设某只鸟属于这三种类别中的一种，其体型特征数据为翼展0.4米，体重0.3公斤，身高0.25米，使用KNN算法计算该鸟最可能的类别，经过归一化，这组数据为(0.2,0.06,0.25)，通过欧式距离计算这只鸟与其他几个样本的距离：

老鹰=sqrt((0.2-1.0)^2 + (0.06-1.0)^2 + (0.25-1.0)^2)≈1.4443

鸽子=sqrt((0.2-0.25)^2 + (0.06-0.1)^2 + (0.25-0.3)^2)≈0.0812

麻雀=sqrt((0.2-0.1)^2 + (0.06-0.01)^2 + (0.25-0.1)^2)≈0.1871

通过距离比对，这只鸟的特征数据与鸽子距离最近，那么最后的分类结果就是鸽子这个类别。当然实际应用中，考虑到超参数K的取值时，计算过程会比这更复杂一些。还是以上面鸟类分类，当样本更多时，输入一组数据，取K=3，假如得到的三个距离为(0.03,0.12,0.15)，三个距离分别对应(麻雀，鸽子，鸽子)。

如果直接采用类别出现最大概率，麻雀占1/3，鸽子占2/3，输出结果即鸽子。

如果采用距离加权进行计算，距离之和为0.3，距离=占比*距离权重，某个类别的距离权重=(总距离-某类总距离)/总距离。

麻雀距离=(1/3)*(0.3-0.03)/0.3=0.3

鸽子距离=(2/3)*(0.3-0.27)/0.3=0.066

通过距离加权后分类结果为麻雀。以上就是KNN算法在分类预测中的应用浅析，其他的应用实现还包括使用KNN进行回归分析等。