数据预处理插补缺失值及比较不同方法的优劣

因为datasets的数据一般都没有空值，所以这里我们人为删除一些数据（随机）

第一步：加载数据并设置空值

import numpy as np
from sklearn.datasets import fetch_california_housing   #加州房价数据集
from sklearn.datasets import load_diabetes  #糖尿病数据集

rng=np.random.RandomState(42)    #生成随机数，RandomState用于获取随机数生成器
X_diabetes,y_diabetes=load_diabetes(return_X_y=True)
X_california,y_california=fetch_california_housing(return_X_y=True)  #获取data
X_california=X_california[:300]  #取前300条目数据
y_california=y_california[:300]
X_diabetes=X_diabetes[:300]
y_diabetes=y_diabetes[:300]

def add_missing_values(X_full,y_full):
    n_samples,n_features=X_full.shape
    #添加所有行的75%（其中，每行只有一个空值）为缺失值？？
    missing_rate=0.75
    n_missing_samples=int(n_samples*missing_rate)  #强制转换为整数（向下取整），设置缺失数据的总数
    missing_samples=np.zeros(n_samples,dtype=bool)
    missing_samples[:n_missing_samples]=True   #将全False数组的前75%赋值为True
    rng.shuffle(missing_samples)    #打乱数据
    missing_features=rng.randint(0,n_features,n_missing_samples)   #返回随机整数型，范围[0,n_features),随机数的尺寸n_missing_samples
    X_missing=X_full.copy()
    X_missing[missing_samples,missing_features]=np.nan    #将X_full的missing_samples为True的行，missing_features列对应的数据赋为空值
    #假设X_full有m行n列
    #那么missing_samples为1*m的由True和False组成的数组（其中75%为True，乱序）
    #missing_features为1*n_missing_samples的0-n_features（列数——特征数）的随机整数数组
    y_missing=y_full.copy()
    return X_missing,y_missing

X_miss_california,y_miss_california=add_missing_values(X_california,y_california)
X_miss_diabetes,y_miss_diabetes=add_missing_values(X_diabetes,y_diabetes)
import pandas as pd
df1=pd.DataFrame(X_miss_california)
print(df1)
df2=pd.DataFrame(y_miss_california)
print(df2)

不难知道，这里缺失值的类型是完全随机缺失（MCAR），所以处理缺失值的方法可以是删除行、和对缺失值进行插补，MCAR可以用的插补方法有很多，这里主要练习比较最近邻插补，均值插补，单变量插补（这里用常数0进行插补），多重插补

第二步：导入需要的模块

rng=np.random.RandomState(0)
from sklearn.ensemble import RandomForestRegressor   #机器学习集成算法——随机森林回归器——用于插值
from sklearn.experimental import enable_iterative_imputer  # noqa   迭代插补
from sklearn.impute import SimpleImputer, KNNImputer, IterativeImputer   #单变量插补，KNN插补，多重插补
from sklearn.model_selection import cross_val_score    #交叉验证评分——选择最优的检查验证方法？
from sklearn.pipeline import make_pipeline           #管道建造，将多个处理步骤合并为单个Scikit-Learn估计器。

N_SPLITS = 4
regressor = RandomForestRegressor(random_state=0)

 第三步：定义函数，后续用于求不同算法下交叉验证的分数

def get_scores_for_imputer(imputer, X_missing, y_missing):   #插值方法，数据
    estimator = make_pipeline(imputer, regressor)    #将插补方法和回归器合并为单个估计器——即下面需要使用交叉验证的算法（对该算法进行交叉验证）
    impute_scores = cross_val_score(
        estimator, X_missing, y_missing, scoring="neg_mean_squared_error", cv=N_SPLITS
    )        #需要使用交叉验证的算法——估计器，数据——含缺失值的数据，评价指标——均方误差（MSE），交叉验证可迭代的次数
    return impute_scores


x_labels = []

mses_california = np.zeros(5)
stds_california = np.zeros(5)
mses_diabetes = np.zeros(5)
stds_diabetes = np.zeros(5)

第四步：估计原始数据的分数

def get_full_score(X_full, y_full):
    full_scores = cross_val_score(
        regressor, X_full, y_full, scoring="neg_mean_squared_error", cv=N_SPLITS
    )        #需要使用交叉验证的算法——估计器，数据——原始数据，评价指标——均方误差（MSE）
    return full_scores.mean(), full_scores.std()


mses_california[0], stds_california[0] = get_full_score(X_california, y_california)
mses_diabetes[0], stds_diabetes[0] = get_full_score(X_diabetes, y_diabetes)
x_labels.append("Full data")

第五步：分别计算不同插补方法下交叉验证的分数

（1）单变量插补（fill_value=0）

 注：add_indicator：boolean，（默认）False，True则会在数据后面加入n列由0和1构成的同样大小的数据，0表示所在位置非缺失值，1表示所在位置为缺失值。

### 将缺失值替换为0——单变量插补

def get_impute_zero_score(X_missing, y_missing):

    imputer = SimpleImputer(
        missing_values=np.nan, add_indicator=True, strategy="constant", fill_value=0   #add_indicator=True——见注释
    )         #插补方法——单变量插补，fill_value=0——将缺失值插补为0
    zero_impute_scores = get_scores_for_imputer(imputer, X_missing, y_missing)  #调用函数，求单变量插补方法下使用交叉验证所得分数
    return zero_impute_scores.mean(), zero_impute_scores.std()

mses_california[1], stds_california[1] = get_impute_zero_score(  #调用函数，求加州房价（处理后含缺失值）在单变量插补（插值为0）下使用交叉验证所得分数
    X_miss_california, y_miss_california
)
mses_diabetes[1], stds_diabetes[1] = get_impute_zero_score(    #糖尿病……分数
    X_miss_diabetes, y_miss_diabetes
)
x_labels.append("Zero imputation")    #添加副标签 

（2）最近邻插补（KNN插补）

### KNN插补求得分
def get_impute_knn_score(X_missing, y_missing):
    imputer = KNNImputer(missing_values=np.nan, add_indicator=True)
    knn_impute_scores = get_scores_for_imputer(imputer, X_missing, y_missing)  #调用函数，求KNN插补方法下使用交叉验证所得分数
    return knn_impute_scores.mean(), knn_impute_scores.std()

mses_california[2], stds_california[2] = get_impute_knn_score(   #调用函数，求加州房价（处理后含缺失值）在KNN插补（插值为0）下使用交叉验证所得分数
    X_miss_california, y_miss_california
)
mses_diabetes[2], stds_diabetes[2] = get_impute_knn_score(
    X_miss_diabetes, y_miss_diabetes
)
x_labels.append("KNN Imputation")   #添加标签

（3）平均值插补

def get_impute_mean(X_missing, y_missing):
    imputer = SimpleImputer(missing_values=np.nan, strategy="mean", add_indicator=True)
    mean_impute_scores = get_scores_for_imputer(imputer, X_missing, y_missing)
    return mean_impute_scores.mean(), mean_impute_scores.std()


mses_california[3], stds_california[3] = get_impute_mean(
    X_miss_california, y_miss_california
)
mses_diabetes[3], stds_diabetes[3] = get_impute_mean(X_miss_diabetes, y_miss_diabetes)
x_labels.append("Mean Imputation")

（4）迭代插补

### 迭代插补得分
def get_impute_iterative(X_missing, y_missing):
    imputer = IterativeImputer(
        missing_values=np.nan,
        add_indicator=True,
        random_state=0,
        n_nearest_features=3,  #用于估计缺失值的其他要素的数量——每个功能列，插补过程中，相邻要素不一定最近，但绘制的概率与每个的相关性成正比插补目标特征。
        max_iter=1,
        sample_posterior=True,  #是否从 （高斯）预测后验中采样 每个插补的拟合估计器。如果用于多次插补则设置，如果设置，则估计器的方法必须支持。
    )
    iterative_impute_scores = get_scores_for_imputer(imputer, X_missing, y_missing)
    return iterative_impute_scores.mean(), iterative_impute_scores.std()

mses_california[4], stds_california[4] = get_impute_iterative(
    X_miss_california, y_miss_california
)
mses_diabetes[4], stds_diabetes[4] = get_impute_iterative(
    X_miss_diabetes, y_miss_diabetes
)
x_labels.append("Iterative Imputation")
#print(type(mses_diabetes))   
mses_diabetes = mses_diabetes * -1   #为什么乘以-1？？？
mses_california = mses_california * -1

# 注：

# 迭代插补是指将每个特征建模为其他特征函数的过程，例如预测缺失值的回归问题。每个特征都是依次输入的，允许在预测后续特征时将先前的输入值用作模型的一部分。

# 这就是迭代的过程，因为这个过程需要重复多次，允许在估计所有特征的丢失值时计算丢失值的不断改进的估计值。

# 这种方法通常被称为完全条件规范（FCS）或链式方程（MICE）的多元插补。

第六步：将结果可视化

### 将结果可视化
import matplotlib.pyplot as plt

n_bars = len(mses_diabetes)   #糖尿病（含缺失数据）插补过后交叉验证分数的均值ndarray数组的长度
xval = np.arange(n_bars)

colors = ["r", "g", "b", "orange", "black"]

# plot diabetes results
plt.figure(figsize=(12, 6))
ax1 = plt.subplot(121)  #将画布分为1行2列，当前位置为1
for j in xval:
    ax1.barh(    #barh表示绘制水平方向的条形图
        j,       #即参数y，表示直方图在y轴上的位置
        mses_diabetes[j],  #即参数width，表示直方图的具体数值，此处即为对应的验证分数的均值
        xerr=stds_diabetes[j],      #xerr指定x轴水平的误差
        color=colors[j],
        alpha=0.6,
        align="center",  #“居中”：将条形图居中放在 y 位置。
    )

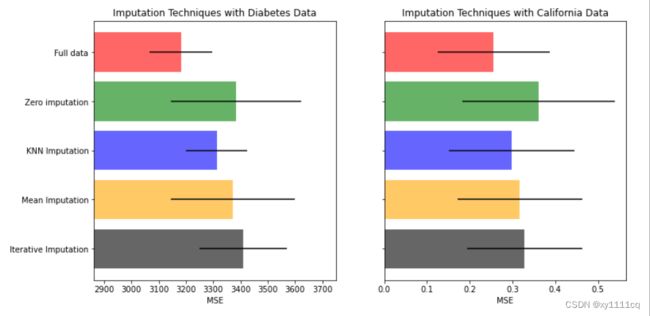
ax1.set_title("Imputation Techniques with Diabetes Data")
ax1.set_xlim(left=np.min(mses_diabetes) * 0.9, right=np.max(mses_diabetes) * 1.1)   #x轴范围最小值为验证分数平均值最小值的0.9倍，最大值为验证分数最大值的1.1倍
ax1.set_yticks(xval)    #设置刻度
ax1.set_xlabel("MSE")   
ax1.invert_yaxis()      #y轴反向
ax1.set_yticklabels(x_labels)   #以x_labels为标签设置刻度（赋值给之前已经设置过的）

# plot california dataset results
ax2 = plt.subplot(122)   #将画布分为1行2列，当前位置为1
for j in xval:
    ax2.barh(
        j,
        mses_california[j],
        xerr=stds_california[j],
        color=colors[j],
        alpha=0.6,
        align="center",
    )

ax2.set_title("Imputation Techniques with California Data")
ax2.set_yticks(xval)
ax2.set_xlabel("MSE")
ax2.invert_yaxis()
ax2.set_yticklabels([""] * n_bars)

plt.show()
​
#注：
#已知：MSE的值越小，说明预测模型描述实验数据具有更好的精确度。¶
#糖尿病数据（除原始数据外），KNN插补交叉验证的MSE的均值与标准差都最小
#加州房价数据（除原始数据外），也是KNN插补交叉验证的MSE的均值与标准差都最小
​