不做调包侠，手撕KNN算法

啥是KNN算法

KNN是最简单的分类算法之一，在给定样本数据和标签的情况下，判定新来的一个数据属于哪一个标签。如何判断呢？关键值在于K，所谓K就是从距离新来数据最近的样本数据中选取K个数据，我们来数一数这K的样本数据对应的标签，哪个标签占比高，那就把该新来的数据归为哪个标签。
基本算法步骤：

1. 设新来数据为x，计算x与所有数据集S中样本的距离。距离是欧式距离，哈密顿距离，根据具体业务而不同。
2. 找出距离最近的K个样本，并查看对应的标签
3. 看哪个标签在K中占比高，则把x记为哪个标签。

手撕KNN算法代码

初始化样本

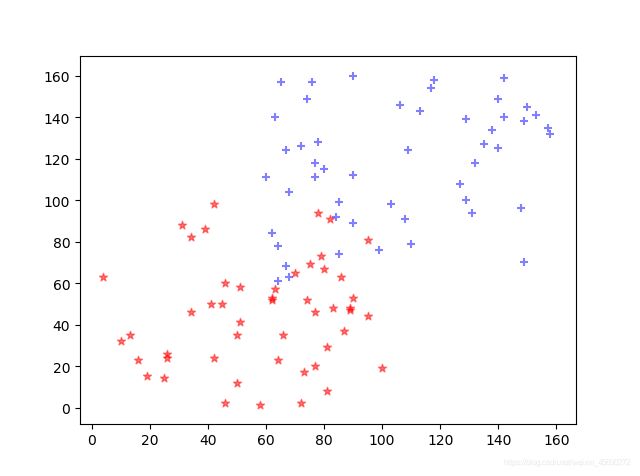
构建一组样本数据，样本格式为[point,label,distance],分别存放点坐标，标签和距离。初始化数据。samples0和samples1分别对应标签为0和1的数据集。samples=samples0+samples1为总体数据。

import random
import matplotlib.pyplot as plt
import math
samplesNum=50
samples=[]
samples0=[]
samples1=[]
for i in range(samplesNum):
    point = [random.randint(0, 100), random.randint(0, 100)]
    samples0.append([point, 0, 0])
for i in range(samplesNum):
    point = [random.randint(60, 160), random.randint(60, 160)]
    samples1.append([point, 1, 0])
samples=samples0+samples1

样本数据大概长这样

KNN算法

我们用KNN算法返回inputTest这个点位的标签。

def distEclud(A,B):
    return math.sqrt(math.pow(A[0]-B[0],2)+math.pow(A[1]-B[1],2))

def classfiyKNN(inputTest,dataSet,K):
    labelsList=[]
    for i in range(len(dataSet)):
        dataSet[i][2]=distEclud(inputTest,dataSet[i][0])
    dataSet.sort(key=lambda samp: samp[2],reverse=False)
    labelsList=[0,1]
    labelsNum=[0,0]
    for i in range(K):
        for j in labelsList:
            if dataSet[i][1]==labelsList[j]:
                labelsNum[j]=labelsNum[j]+1
                break
    labelIndex=labelsNum.index(max(labelsNum))
    return labelsList[labelIndex]

实验几个数据

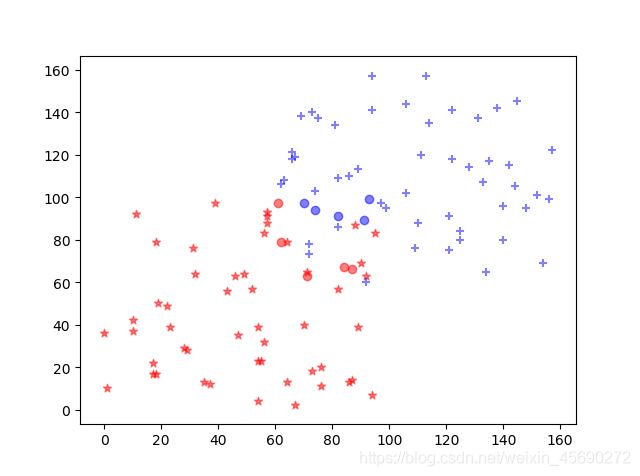
我们生成10个测试数据，看下情况。其中圆形的数据为测试数据。对应的颜色即为其分类。

K=10
testSample=[]
for i in range(10):
    point = [random.randint(60, 100), random.randint(60, 100)]
    testSample.append(point)
for t in testSample:
    resultlabel = classfiyKNN(t, samples, K)
    plt.scatter(t[0], t[1], marker=markers[2], c=color[resultlabel], alpha=0.5)
plt.show()

K的选择

KNN算法最关键的是确定K值。我们通过对原始样本处理，找到最合适的K值。通过测试我们看到在K取1,2，3左右时，错误率较低。

TestNum=int(samplesNum*0.4)

TestSamples0=random.sample(samples0,TestNum)
TestSamples1=random.sample(samples1,TestNum)
for ts in TestSamples0:
    samples0.remove(ts)

for ts in TestSamples1:
    samples1.remove(ts)

TestSample=TestSamples0+TestSamples1
TrainSample=samples1+samples1
print("TestSample：",len(TestSample))
print("TrainSample：",len(TrainSample))
error_rate=[]
Kx=[]
for K in range(20):
    errorNum=0
    Kx.append(K)
    for TS in TestSample:
        resultlabel = classfiyKNN(TS[0], samples, K)
        if resultlabel!=TS[1]:
            errorNum+=1
    error_rate.append(round(errorNum/len(TestSample),2))

plt.plot(Kx,error_rate,'g')

print(error_rate)
plt.show()