C++编写解决八数码问题

**C++编写解决八数码问题##

一、需求与规则说明

八数码问题又称重排九宫问题，在一个 33 的棋盘上，随机放置 1 到 8 的数
字棋子，剩下一个空位，如图所示。数字可以移动到空位（编程时，空位可用 0
代替，且可以理解为是空位的上、下、左、右移动），经过若干次移动后，棋局
到达指定目标状态。

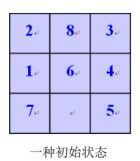
说明：重排九宫问题，对任意给定初始状态，可达下图所示两个目标之一，
不可互换。
目标一：如下图 G

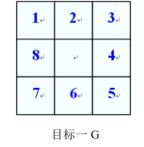
目标二：如下图 G1 或 G2

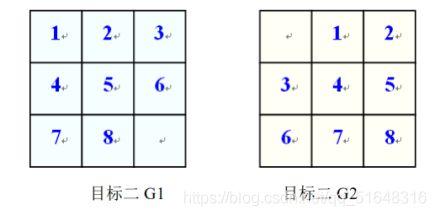
要求：
① 编程求解问题；
② 给出中间状态；
③ 给出解序列（函数调用序列）

二、设计

广搜遍历：
（1）用户输入八数码的初始状态后，将状态压缩为一个整数。
（2）系统将此数据在全排列中的位置记为被访问（用于判重），同时将次数据储存入结构体数组中。
（3）首先判断数据是否已经是目标状态，若是，则结束函数。
（4）若不是，系统将数据转化为二维数组，并记录八数码中0在数组中的位置，然后在数组中依次向四个方向扩展。若越界则直接进行下个方向的扩展，其余继续扩展。
（5）扩展过程中将0与扩展方向的数据交换，转化为整数并判断此数据在全排列中的位置是否记为已访问，若未访问过，将此数据记录入结构体数组中，并判断该数据是否为目标状态。否则跳出此次扩展，最后数组交换为扩展前的数组，继续向其他方向扩展。
（6）该数据的四个方向扩展完成后，继续扩展结构体数组中下一个数据，重复（4）（5）过程，直至达到目标状态或不能继续扩展的状态。
（7）若可以达到目标状态，则通过子节点递归寻找父节点，矩阵输出每个节点所储存的数据，若不能则结束

三、源代码

注意：需要用到easyx数据库，可以在
https://blog.csdn.net/edc370/article/details/79944550?utm_source=app
下载，博主讲的很详细的

#include      //C++标准库
#include    //图形汇编
//#include     //windows窗口控制
using namespace std;

struct Q {
	int val;
	int father;
}que[110000];      //bfs所用队列

bool flag[362880] = { false };    //判重
//康托展开判重
int Cantor(int num)
{
	int jc[9] = { 1,1,2,6,24,120,720,5040,40320 }; //分别记录0~8的阶乘
	int ans = 1;       //记录全排列的位置，从1开始
	char str[9];       //将原数据数组转化为字符数组
	for (int i = 8; i >= 0; i--)
	{
		str[i] = num % 10;
		num /= 10;
	}
	for (int i = 0; i < 9; i++)
	{
		int max = 0;
		for (int j = i + 1; j < 9; j++)
		{

			if (str[i] > str[j])
			{
				max++;
			}
		}
		ans += max * jc[8 - i];
	}
	return ans;
}

int start, aim;
int dx[5] = { 0,0,1,0,-1 };
int dy[5] = { 0,1,0,-1,0 };

int bfs()           //广搜遍历
{
	flag[Cantor(start)] = true;
	que[1].val = start;
	int head = 0, tail = 1;
	int now = start;          //当前状态
	if (start == 123456780 || start == 123804765 || start == 123456780)
	{
		aim = start;
		return tail;
	}
	while (head < tail)
	{
		int zero_x, zero_y;     //0 的位置
		head++;
		now = que[head].val;
		int a[5][5] = { 0 };
		//将状态转化成二维数组
		for (int i = 3; i >= 1; i--)
			for (int j = 3; j >= 1; j--)
			{
				a[i][j] = now % 10;
				now /= 10;
				if (a[i][j] == 0)
					zero_x = i, zero_y = j;
			}
		for (int i = 1; i <= 4; i++)
		{
			if (a[zero_x + dx[i]][zero_y + dy[i]])
			{
				aim = 0;
				int x = zero_x + dx[i];
				int y = zero_y + dy[i];
				swap(a[x][y], a[zero_x][zero_y]);

				for (int i = 1; i <= 3; i++)
					for (int j = 1; j <= 3; j++)
						aim = aim * 10 + a[i][j];
				if (!flag[Cantor(aim)])
				{
					que[++tail].val = aim;
					que[tail].father = head;
					flag[Cantor(aim)] = 1;
				}
				swap(a[x][y], a[zero_x][zero_y]);
				if (aim == 123456780 || aim == 123804765 || aim == 12345678)   //达成目标状态 
				{
					return tail;
				}
			}
		}
	}
	cout << "不能达成目标" << endl;
	return -1;
}
void dfs(int now)       //递归输出解
{
	
	if (now == 0)
	{
		return;
	}
	dfs(que[now].father);
	int a[5][5];
	int num = que[now].val;
	for (int i = 3; i >= 1; i--)
		for (int j = 3; j >= 1; j--)
		{
			a[i][j] = num % 10;
			num /= 10;
		}
	for (int i = 1; i <= 3; i++)
	{
		for (int j = 1; j <= 3; j++)
			cout << a[i][j] << ' ';
		cout << endl;
	}
	cout << "**************" << endl;
}

void show(int now)     //与dfs函数基本相同 用于演示过程
{
	static int temp = 0;
	if (temp == 0)
	{
		initgraph(300, 300);      //绘制界面
		setbkcolor(WHITE);
		cleardevice();
		setlinecolor(BLACK);
		settextcolor(BLACK);
		setbkmode(TRANSPARENT);
		settextstyle(40, 20, "宋体");
		temp++;
	}
	if (now == 0)
	{
		return;
	}

	show(que[now].father);

	int num = que[now].val;
	int arr[3][3];
	for (int i = 2; i >= 0; i--)
		for (int j = 2; j >= 0; j--)
		{
			arr[i][j] = num % 10 + 48;
			num /= 10;
		}

	for (int i = 0; i < 4; i++)
	{
		line(100 * i, 0, 100 * i, 300);
		line(0, 100 * i, 300, 100 * i);
	}

	for (int i = 0; i <= 2; i++)
		for (int j = 0; j <= 2; j++)
			outtextxy(100 * j + 35, 100 * i + 30, char(arr[i][j]));

	Sleep(1000);
	cleardevice();

	if (que[now].val == 123456780 || que[now].val == 123804765 || que[now].val == 12345678)
	{
	closegraph();
	}
}
int main()
{
	cout << "请输入八数码矩阵：" << endl;
	int t;
	//输入初始状态并进行状态压缩 
	for (int i = 1; i <= 9; i++)
	{
		cin >> t;
		start *= 10;
		start += t;
	}
	int end = bfs();
	if (end == -1)
	{
		return 0;
	}
	//演示部分 
	cout << "\n" << "即将开始演示" << endl;
	system("pause");
	show(end);
	Sleep(500);
	//演示部分结束
	cout << "\n" << "演示完毕，按任意键查看全过程" << endl;
	system("pause");
	system("cls");
	cout << "**************" << endl;
	if (aim == 123804765)
		cout << "该初始状态可达成目标一" << endl;
	else
		cout << "该初始状态可达成目标二" << endl;
	cout << "**************" << endl;
	dfs(end);

	system("pause");
	return 0;
}

总结

学习广度优先搜搜索，八数码问题是一个很好的案例，可以很好地掌握广搜，同时,也可以学习深度优先搜索，与广搜相类似。
提示：在学会以上的基础上，可以学习Astar算法，启发式算法，个人学习编程时间不长，在看了许多博主的发表后，感觉启发式算法像是在广搜的基础上加了一些判断条件，试着写了，确实减少的遍历的路径，但不太肯定，希望有人可以指点。
个人学习时间不长，如有错误和改进，请一定要提出来，谢谢