EM算法与变分推断

一、EM算法

目的：找到含有潜变量模型的极大似然解
应用背景：对于某些数据直接估计模型参数较为困难，但通过引入潜变量可以降低模型的求解难度。但引入潜变量后怎样来求解？——EM算法。

1. 直观感受EM算法

对对数似然函数$\log P(X|\theta )$有$\log P(X|\theta )=\log {\sum }_{Z}P(X,Z|\theta )$，这样处理的目的是为了引入潜变量，但这样同时也会导致如下两个问题

1. 求和操作在对数里面使得对数运算无法直接作用在联合分布上
2. 由于$Z$是隐变量，我们无法得知关于它的信息

为了解决以上这两个问题，我们可以将$\arg {\max }_{\theta }\log P(X|\theta )$近似为
$$\arg \underset{\theta }{\max }\sum _{Z}P(Z|X,\theta )\log P(X,Z|\theta )\text{\hspace{1em}(1)}$$
（为什么可以这样近似在后面会讲述），近似后的目标函数相比于原目标函数的优势在于

1. 求和符号从对数里面提到了对数外面降低了处理难度
2. ${\sum }_{Z}P(X,Z|\theta )$不好直接处理，但对转化后的目标函数，我们可以利用已知数据对$Z$进行推断得到$P(Z|X,\theta )$，再利用推断得到的$P(Z|X,\theta )$来进行求和

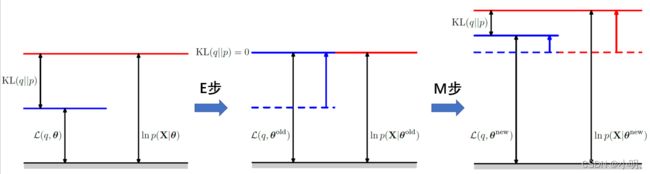
在近似处理结束后，对于目标${\theta }^{\ast }=\arg {\max }_{\theta }{\sum }_{Z}P(Z|X,\theta )\log P(X,Z|\theta )$，可以采用交替更新的方式来对目标进行求解，具体来说求解算法包括两步（这两步分别被称为E步和M步）：

1. E步：在E步中我们利用数据和现有参数（记为${\theta }^{old}$）来对Z的概率进行推断，并用得到的$P(Z|X,{\theta }^{old})$计算$Q(\theta ,{\theta }^{old})={\sum }_{Z}P(Z|X,{\theta }^{old})\log P(X,Z|\theta )$，因为这里利用$P(Z|X,{\theta }^{old})$对$\log P(X,Z|\theta )$进行了期望运算，进而这一步也被称为E（Expectation）步。
2. M步：在M步中对于E步所获得的期望$Q(\theta ,{\theta }^{old})$，我们寻找最优的新参数${\theta }^{new}=\arg {\max }_{\theta }Q(\theta ,{\theta }^{old})$，并令${\theta }^{old}={\theta }^{new}$在这一步骤中因为涉及到了最大化期望，因而它也被称为M（Maximization）步

通过不断交替重复E步和M步，直至收敛条件满足或达到最大迭代次数，得到参数$\theta$

2. 从数学角度推导EM

在这里我们假设潜变量$Z$服从分布$q(Z)$则
$$\begin{array}{rl}\log P(X|\theta )=\sum _{Z}q(Z)\log P(X|\theta )& =\sum _{Z}q(Z)\log (\frac{P(X|\theta )}{P(X,Z|\theta )}\frac{P(X,Z|\theta )}{q(Z)}q(Z))\\ & =\sum _{Z}q(Z)\log (\frac{q(Z)}{P(Z|X,\theta )})+\sum _{Z}q(Z)\log \frac{P(X,Z|\theta )}{q(Z)}\\ & =\sum _{Z}q(Z)\log (\frac{q(Z)}{P(Z|X,\theta )})+\sum _{Z}q(Z)\log P(X,Z|\theta )-\sum _{Z}q(Z)\log q(Z)\\ & =KL(q(Z)||P(Z|X,\theta ))+\sum _{Z}q(Z)\log P(X,Z|\theta )+H(Z)\end{array}$$
这里注意到$H(Z)$是与$X,\theta$无关的，我们不考虑它，从而得到一个新的目标函数
$$\mathcal{L}=KL(q(Z)||P(Z|X,\theta ))+\sum _{Z}q(Z)\ln P(X,Z|\theta )\text{\hspace{1em}(2)}$$
注意式（2）中的第二部分与式（1）很像。在这里，最大化$\mathcal{L}$等价于最大化似然函数$\log P(X|\theta )$. 对目标函数$\mathcal{L}$我们可以采取两步优化的方式来最大化。

1. 优化KL散度：$\mathcal{L}$在$\theta$（$\theta ={\theta }^{old}$）给定的时候是一个定值，此时最小化KL散度可以使${\sum }_{Z}q(Z)\log P(X,Z|{\theta }^{old})$最大。由KL散度的性质不难得到当$q(Z)=p(Z|X,{\theta }^{old})$时KL散度最小其值为0. 当$q(Z)=p(Z|X,{\theta }^{old})$，$KL(q(Z)||P(Z|X,{\theta }^{old}))=0$，这时$\mathcal{L}={\sum }_{Z}q(Z|X,{\theta }^{old})\log P(X,Z|{\theta }^{old})$，正好是EM算法E步的Q函数的形式。
2. 最大化$\mathcal{L}$ ：$\arg {\max }_{\theta }{\sum }_{Z}P(Z|X,{\theta }^{old})\log P(X,Z|\theta )$，此时最大化$\mathcal{L}$等价于最大化似然函数。同时由于$\theta$的更新导致$q(Z)=P(Z|X,{\theta }^{old})\ne P(Z|X,{\theta }^{new})$，这会使得KL散度不再为0导致$\mathcal{L}$上升，同时KL不为0又使得我们可以进行新的一轮优化。这也是EM算法为什么可以最大化似然函数的原因。

整个过程的示意图如下：

注：

1. 省略$H(Z)$是否合理：在E步中通过$q(Z)=P(Z|X,{\theta }^{old})$来估计$q(Z)$。在得到$q(Z)$的估计后$\log P(X|\theta )$变为$\log P(X|\theta )={\sum }_{Z}q(Z|X,{\theta }^{old})\log P(X,Z|\theta )+{\sum }_{Z}q(Z|X,{\theta }^{old})\log q(Z|X,{\theta }^{old})$。显然$H(Z)$在这个时候是定值与$\theta$无关，因此在优化时省略掉也是合理的。
2. 在这里可以把${\sum }_{Z}q(Z)\log P(X|\theta )$换为$E_{q(Z)}\log P(X|\theta )$也成立（后者是更一般的情况）。

二、变分推断

变分推断（Variational Inference, VI）
目的：近似推断后验分布$P(Z|X)$
核心思想：假设一个密度族，然后再在密度族中找出一个与目标密度最为接近的密度。（一般两个密度之间的距离用KL散度刻画。）

1. ELBO的引入

这里尝试从两个不同的角度分别引入ELBO

a. 近似推断

由于对$P(Z|X)$的推断较为困难（潜在空间维度高或$P(Z|X)$的形式复杂）。因此尝试在一个密度函数族$Q$中找到一个$q(Z)$使其与$P(Z|X)$尽可能接近即$q^{\ast }(Z)=\arg {\min }_{q(Z)\in Q}KL(q(Z)||P(Z|X))$。其中(这一部分的$E[\cdot ]$是关于分布$q(Z)$求期望)
$$\begin{array}{rl}\arg \underset{q^{\ast }(Z)\in Q}{\min }KL(q(Z)||P(Z|X))& =E[\log q(Z)]-E[\log P(Z|X)]\\ & =E[\log q(Z)]-E[\log P(X,Z)]+E[\log P(X)]\end{array}$$
但这个目标并不好优化，因为其中含有$P(X)$，而$P(X)={\int }_{Z}P(X,Z)dZ$计算起来较为困难。但我们注意到$P(X)$与$q(Z)$没有直接联系，因此对目标函数进行转化，得到以下等价目标函数证据下界 (evidence lower bound, ELBO)。
$$ELBO(q)=E[\log P(X,Z)]-E[\log q(Z)]$$
ELBO等于负的KL散度加上$\log P(X)$，因此最大化$ELBO(q)$等价于最小化$KL(q(Z)||P(Z|X))$。此外对ELBO的表达式还可以有以下直观理解：

1. ELBO可以进行如下转化
   $$\begin{array}{rl}ELBO(q)& =E[\log P(X,Z)]-E[\log q(Z)]\\ & =E[\log P(X|Z)]+E[\log P(Z)]-E[\log q(Z)]\\ & =E[\log P(X|Z)]-KL(q(Z)||P(Z))\end{array}$$
   其中第一项为对数似然要求潜变量尽可能解释观测数据的分布，第二项为KL散度要求让后验$q(Z)$分布尽可能接近先验分布$P(Z)$

2. $\log P(X)\ge ELBO(q)$：$\log P(X)=ELBO(q)+KL(q(Z)||P(Z|X))$，而KL散度大于等于0。从这里我们也可以知道ELBO名字的由来。

b. 极大似然

计算$P(Z|X)$的目的是在合适的条件下使$\log P(X)$（似然函数）最大。因此我们可以基于$\log P(X)$来推导$ELBO(q)$
$$\begin{array}{rl}\log P(X)& =\int q(Z)\log P(X)dZ\\ & =\int q(Z)\log \frac{P(X)}{P(X,Z)}\frac{P(X,Z)}{q(Z)}q(Z)\\ & =\int q(Z)\log \frac{q(Z)}{P(Z|X)}dZ+\int q(Z)\log \frac{P(X,Z)}{q(Z)}dZ\\ & =KL(q(Z)||p(Z|X))+\mathcal{L}(q)\end{array}$$
其中$\mathcal{L}(q)=\int q(Z)\log \frac{P(X,Z)}{q(Z)}dZ=E[\log p(X,Z)]-E[\log q(Z)]$为$ELBO(q)$。注意到，在样本给定的时候$\log P(X)$是一个定值，因此在这种情况下最大化$\mathcal{L}(q)$等价于最小化$KL(q(Z)||p(Z|X))$

2.几种特殊的变分推断

a. 平均场变分推断

平均场假设（Mean-Field Assumption）：$q(Z)={\prod }_i{q}_i(Z_i)$ 这里$Z_i$并非特指单个随机变量，而可以理解成是一个团。

基于平均场假设
$$\begin{array}{rl}\mathcal{L}(q)& =\int q(Z)\log P(X,Z)dZ-\int q(Z)\log q(Z)dZ\\ & =\int q_j(\log p(X,Z)\prod _{i\ne j}{q}_{i}d{Z}_i)d{Z}_j-\int q_j\log q_{j}d{Z}_j+\text{const}\\ & =\int q_j\log \tilde{p}(X,Z_j)d{Z}_j-\int q_j\log q_{j}d{Z}_j+\text{const}\end{array}$$
这里$\log \tilde{p}(X,Z_j)=E_{i\ne j}[\log P(X,Z)]+\text{const}$。在这里保持$\{q_{i\ne j}\}$固定，关于分布$q_j(Z_j)$来最大化$\mathcal{L}(q)=-KL(q_j||\tilde{p}(X,Z_j))+\text{const}$。此时最大化$\mathcal{L}$等价于最小化KL散度。由KL散度的定义易知$\log q_j^{\ast }(Z_j)=E_{i\ne j}[\log P(X,Z)]+\text{const}$，于是我们可以得到如下方程组
$$q_j^{\ast }(Z_j)=\frac{\exp (E_{i\ne j}[\log P(X,Z)])}{\int \exp (E_{i\ne j}[\log P(X,Z)])d{Z}_j}(j=1,\cdots ,n)$$
这个方程组无显示解，因此采用一种交替迭代的方法来求解（CAVI）具体表现为：在给出一个恰当的初始话后，循环更新$q(Z_i)$（用$q^{\ast }(Z_i)$给出估计）。

b. 随机梯度变分推断

对目标函数：$\hat{q}=\arg {\min }_{q}KL(q||p)=\arg \min \mathcal{L}(q)$，设$Z$服从分布$q_{\varphi }(Z)$，这样目标函数变为$\hat{\varphi }=\arg {\min }_{\varphi }\mathcal{L}(\varphi )$
$$\begin{array}{rl}{\nabla }_{\varphi }\mathcal{L}(\varphi )& ={\nabla }_{\varphi }{E}_{q_{\varphi }}[\log P_{\theta }(X,Z)-\log q_{\varphi }]\\ & =E_{q_{\varphi }}[{\nabla }_{\varphi }(\log P_{\theta }(X,Z)-\log q_{\varphi })]\\ & =\int {\nabla }_{\varphi }{q}_{\varphi }(\log P_{\theta }(X,Z)-\log q_{\varphi })dZ+\int q_{\varphi }{\nabla }_{\varphi }[\log P_{\theta }(X,Z)-\log q_{\varphi }]dZ\end{array}$$
这里$\int q_{\varphi }{\nabla }_{\varphi }[\log P_{\theta }(X,Z)-\log q_{\varphi }]dZ=-\int q_{\varphi }{\nabla }_{\varphi }\log q_{\varphi }dZ=-\int {\nabla }_{\varphi }{q}_{\varphi }dZ=-{\nabla }_{\varphi }\int q_{\varphi }dZ=0$，进而
$$\begin{array}{rl}{\nabla }_{\varphi }\mathcal{L}(\varphi )& =\int q_{\varphi }{\nabla }_{\varphi }\log q_{\varphi }(\log P_{\theta }(X,Z)-\log q_{\varphi })dZ\\ & =E_{q_{\varphi }}[{\nabla }_{\varphi }\log q_{\varphi }(\log P_{\theta }(X,Z)-\log q_{\varphi })]\end{array}\text{\hspace{1em}(3)}$$
注：对于（3）式中的期望计算可以利用MCMC来估计，即记$Z^{(l)}\sim q(z)l=1,2,\cdots ,L$，则${\nabla }_{\varphi }\mathcal{L}(\varphi )=\frac{1}{L}{\sum }_l{\nabla }_{\varphi }\log q_{\varphi }(\log P_{\theta }(X,Z^{(l)})-\log q_{\varphi }(Z^{(l)})$，若采样过程中$Z^{(l)}$过小会导致$\log q_{\varphi }(Z^{(l)})$过大，使得计算不稳定，为了稳定则需要大量采样。

c. 重参数技巧

不妨设$Z=g_{\varphi }(ϵ,X)$，这里$ϵ\sim p(ϵ)$同时有$|q_{\varphi }(Z|X)dZ|=|p(ϵ)dϵ|$，于是我们可以推导
$$\begin{array}{rl}{\nabla }_{\varphi }\mathcal{L}(\varphi )& ={\nabla }_{\varphi }{E}_{q_{\varphi }}[\log P_{\theta }(X,Z)-\log q_{\varphi }]\\ & ={\nabla }_{\varphi }\int [\log P_{\theta }(X,Z)-\log q_{\varphi }]q_{\varphi }dZ\\ & ={\nabla }_{\varphi }\int [\log P_{\theta }(X,Z)-\log q_{\varphi }]p(ϵ)dϵ\\ & =E_{p(ϵ)}[{\nabla }_{\varphi }(\log P_{\theta }(X,Z)-\log q_{\varphi })]\\ & =E_{p(ϵ)}[{\nabla }_Z(\log P_{\theta }(X,Z)-\log q_{\varphi }){\nabla }_{\varphi }{g}_{\varphi }(ϵ,X)]\end{array}$$

注：VI和EM的一个差异，在EM中$\theta$是固定的，$Z$是随机的；但在VI中只有一个随机的$Z$，因此EM可以视为VI的特例。

参考

[1] Blei, D. M., Kucukelbir, A., & McAuliffe, J. D. (2017). Variational inference: A review for statisticians. Journal of the American statistical Association, 112(518), 859-877.
[2] Bishop, C. M., & Nasrabadi, N. M. (2006). Pattern recognition and machine learning (Vol. 4, No. 4, p. 738). New York: springer.
[3]https://www.bilibili.com/video/BV1DW41167vr?spm_id_from=333.999.0.0