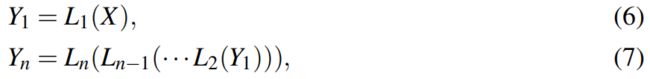G-GhostNet（IJCV 2022）原理与代码解析

paper：GhostNets on Heterogeneous Devices via Cheap Operations

code：https://github.com/huawei-noah/Efficient-AI-Backbones/blob/master/g_ghost_pytorch/g_ghost_regnet.py

前言

本文提出了两种轻量网路，用于CPU端的C-GhostNet和用于GPU端的G-GhostNet。前者就是20年的原版GhostNet，这里只是换了个名字，具体可见GhostNet（CVPR 2020） 原理与代码解析，这里不再详细介绍。本文主要介绍新提出的基于GPU端的G-GhostNet。

存在的问题

之前的轻量型骨干网络大都以降低模型FLOPs为准则专门为CPU设计的，但由于CPU和GPU的硬件架构存在明显的差异，一些FLOPs较小的操作（特别是depth-wise convolution和channel shuffle）在GPU上并不是那么高效。实际上这些操作通常具有较低的arithemetic intensity，即计算和内存操作的比值，无法充分利用GPU的并行计算能力。

本文的创新点

在许多CNN骨干网络的架构中，一个stage通常包含多个卷积层或block，C-GhostNet研究的是一个卷积层生成的特征图中通道信息的冗余，而G-GhostNet研究的是多个block之间的特征相似性和冗余，并通过观察发现跨block的特征冗余是存在的，提出了G-Ghost stage，一个stage的最终输出一部分是和原来一样经过多个block得到的，另一部分通过廉价操作得到，最终将两部分拼接得到输出，大大降低了计算成本。

方法介绍

低FLOPs的操作比如深度可分离卷积在GPU上不那么高效，Radosavovic等人提出用激活activation来衡量网络的复杂度，在GPU上相比于FLOPs延迟和激活的相关性更大，也就是说，如果我们可以删去部分特征图减少激活大概率就能降低网络的延迟。通常一个CNN网络由多个stage构成，每个stage又包含多个block，本文旨在减少stage中的特征冗余大大减少中间特征，从而降低计算成本和内存使用。

对于CNN中的某个stage，有 \(n\) 层比如AlexNet或 \(n\) 个block表示为 \(\left \{ L_{1},L_{2},...,L_{n} \right \} \)，对于输入 \(X\) 第一个block和最后一个block的输出为

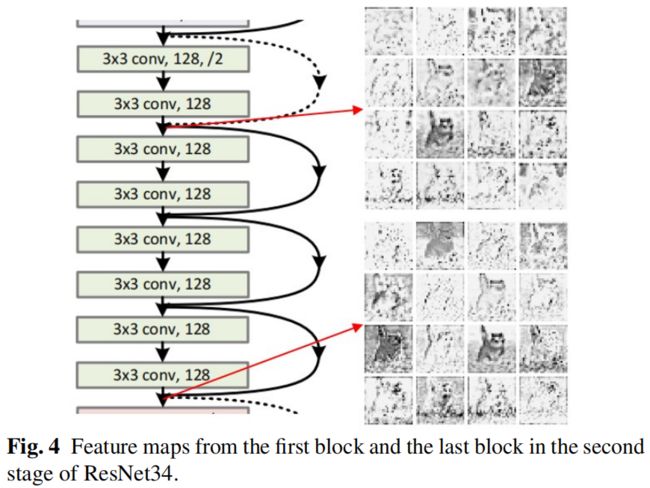
要获得最终的输出 \(Y_{n}\)，输入需要经过多个block的处理，这需要大量的计算。下图是ResNet34的第三个stage中第一个block和最后一个block的输出特征图，尽管最后一个block的输出经过了前5个block的处理，其中有些特征与第一个block的输出仍然非常相似，这意味着这些特征可以通过对低级特征的简单转换来得到。

作者将深层特征分为comlicated特征和ghost特征，前者仍然通过多个block来生成，后者可以通过对浅层特征的简单转换来得到。对于一个有 \(n\) 个block的stage，其输出为 \(X\in \mathbb{R}^{c\times h\times w}\)，我们将复杂特征表示为 \(Y^{c}_{n}\in \mathbb{R}^{(1-\lambda)c\times h\times w}\)，ghost特征表示为 \(Y^{c}_{g}\in \mathbb{R}^{\lambda c\times h\times w}\)，其中 \(0\le \lambda \le 1\)。复杂特征通过 \(n\) 个block得到

其中 \(L'_{2},...,L'_{n}\) 是相比于式(7)宽度为 \((1-\lambda)\times width\) 的thin block。\(Y^{g}_{n}\) 可以通过对 \(Y_{1}\) 的廉价操作 \(C\) 得到

其中廉价操作 \(C\) 可以是1x1或3x3卷积。将 \(Y^{c}_{n}\) 和 \(Y^{g}_{n}\) 拼接起来就得到了最终输出

Intrinsic Feature Aggregation

尽管简单特征可以通过廉价操作近似得到，但式(9)中的 \(Y^{g}_{n}\) 可能缺乏需要多层才能提取到的深层信息，为了弥补缺乏的信息，作者提出用complicated分支的中间特征来提高廉价操作的表示能力。首先提取复杂分支的中间特征 \(Z\in \mathbb{R}^{c'\times h\times w}=[Y^{c}_{2},Y^{c}_{3},...,Y^{c}_{n}]\) 将其按通道concat起来，其中 \(c'\) 是通道总数，如下图所示

通过转换函数 \(\tau \) 对 \(Z\) 进行变换，然后与 \(Y^{g}_{n}\) 进行融合。

转换函数 \(\tau\) 包括一个全局平均池化和一个全连接层

其中 \(W\in \mathbb{R}^{c'\times \lambda c}\)，\(b\in \mathbb{R}^{\lambda c}\) 分别是权重和偏置。

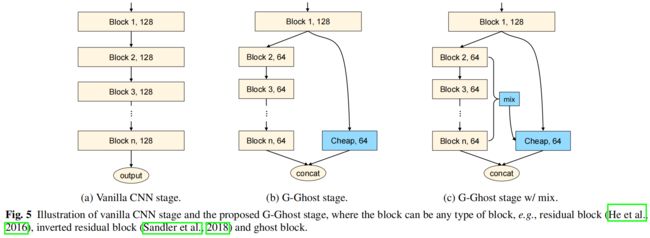
下图分别是原始的CNN结构、没有特征聚合的G-Ghost stage和有特征聚合的G-Ghost stage

代码解析

下面是G-Ghost stage的官方实现，好像和文章中的描述有些出入。forward函数中首先self.base就是上图中的Block 1，出入一是文中Block 1的输出好像是完整的分别进入complicated分支和cheap分支，而实现中是将Block 1的输出按 \(\lambda\) 沿通道分为两部分分别进入两个分支。出入二是从上图可以看出是对Block 2 - Block n进行特征聚合，而实现中还包括Block 1，即代码中的x0。self.merge是转换函数 \(\tau\)，其中全连接层用卷积层实现。

class Stage(nn.Module):
    def __init__(self, block, inplanes, planes, group_width, blocks, stride=1, dilate=False, cheap_ratio=0.5):
        super(Stage, self).__init__()
        norm_layer = nn.BatchNorm2d
        downsample = None
        self.dilation = 1
        previous_dilation = self.dilation
        if dilate:
            self.dilation *= stride
            stride = 1
        if stride != 1 or self.inplanes != planes:
            downsample = nn.Sequential(
                conv1x1(inplanes, planes, stride),
                norm_layer(planes),
            )

        self.base = block(inplanes, planes, stride, downsample, group_width,
                          previous_dilation, norm_layer)
        self.end = block(planes, planes, group_width=group_width,
                         dilation=self.dilation,
                         norm_layer=norm_layer)

        group_width = int(group_width * 0.75)
        raw_planes = int(planes * (1 - cheap_ratio) / group_width) * group_width
        cheap_planes = planes - raw_planes
        self.cheap_planes = cheap_planes
        self.raw_planes = raw_planes

        self.merge = nn.Sequential(
            nn.AdaptiveAvgPool2d(1),
            nn.Conv2d(planes + raw_planes * (blocks - 2), cheap_planes,
                      kernel_size=1, stride=1, bias=False),
            nn.BatchNorm2d(cheap_planes),
            nn.ReLU(inplace=True),
            nn.Conv2d(cheap_planes, cheap_planes, kernel_size=1, bias=False),
            nn.BatchNorm2d(cheap_planes),
        )
        self.cheap = nn.Sequential(
            nn.Conv2d(cheap_planes, cheap_planes,
                      kernel_size=1, stride=1, bias=False),
            nn.BatchNorm2d(cheap_planes),
        )
        self.cheap_relu = nn.ReLU(inplace=True)

        layers = []
        downsample = nn.Sequential(
            LambdaLayer(lambda x: x[:, :raw_planes])
        )

        layers = []
        layers.append(block(raw_planes, raw_planes, 1, downsample, group_width,
                            self.dilation, norm_layer))
        inplanes = raw_planes
        for _ in range(2, blocks - 1):
            layers.append(block(inplanes, raw_planes, group_width=group_width,
                                dilation=self.dilation,
                                norm_layer=norm_layer))

        self.layers = nn.Sequential(*layers)

    def forward(self, input):
        x0 = self.base(input)

        m_list = [x0]
        e = x0[:, :self.raw_planes]
        for l in self.layers:
            e = l(e)
            m_list.append(e)
        m = torch.cat(m_list, 1)
        m = self.merge(m)

        c = x0[:, self.raw_planes:]
        c = self.cheap_relu(self.cheap(c) + m)

        x = torch.cat((e, c), 1)
        x = self.end(x)
        return x