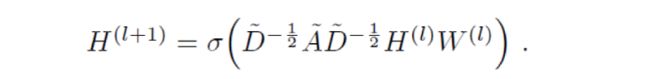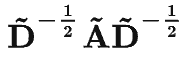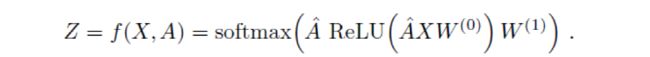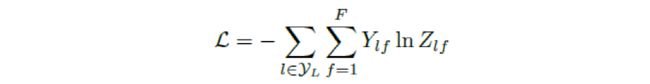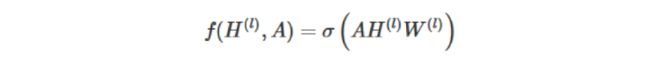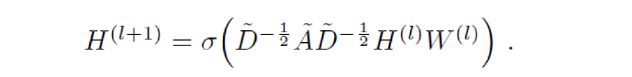GCN详解

目录

一.GCN介绍

二.GCN的应用

三.GCN的原理

四.GCN核心公式的由来

---

一.GCN介绍

CNN的核心在于它的kernel，kernel是一个个小窗口，在图片上平移，通过卷积的方式来提取特征。这里的关键在于图片结构上的平移不变性：一个小窗口无论移动到图片的哪一个位置，其内部的结构都是一模一样的，因此CNN可以实现参数共享。这就是CNN的精髓所在。

再回忆一下RNN系列，它的对象是自然语言这样的序列信息，是一个一维的结构，RNN就是专门针对这些序列的结构而设计的，通过各种门的操作，使得序列前后的信息互相影响，从而很好地捕捉序列的特征。

上面讲的图片或者语言，都属于欧式空间的数据，因此才有维度的概念，欧式空间的数据的特点就是结构很规则。但是现实生活中，其实有很多很多不规则的数据结构，典型的就是图结构，或称拓扑结构，如社交网络、化学分子结构、知识图谱等等；即使是语言，实际上其内部也是复杂的树形结构，也是一种图结构；而像图片，在做目标识别的时候，我们关注的实际上只是二维图片上的部分关键点，这些点组成的也是一个图的结构。

图的结构一般来说是十分不规则的，可以认为是无限维的一种数据，所以它没有平移不变性。每一个节点的周围结构可能都是独一无二的，这种结构的数据，就让传统的CNN、RNN瞬间失效。所以很多学者从上个世纪就开始研究怎么处理这类数据了。这里涌现出了很多方法，例如GNN、DeepWalk、node2vec等等，GCN只是其中一种。

GCN，图卷积神经网络，实际上跟CNN的作用一样，就是一个特征提取器，只不过它的对象是图数据。GCN精妙地设计了一种从图数据中提取特征的方法，从而让我们可以使用这些特征去对图数据进行节点分类（node classification）、图分类（graph classification）、边预测（link prediction），还可以顺便得到图的嵌入表示（graph embedding），可见用途广泛。

二.GCN的应用

GCN 的作用实际上和 CNN 差不多，都是一个特征提取器，只不过 GCN 的处理对象更加复杂。GCN 设计了一种从图数据当中提取特征的方法，从而可以应用到对图数据进行节点分类、图分类、边预测、还可以得到图的嵌入表示。

二.GCN的原理

假设有一个图结构，图中有N个节点（node），每个节点都有自己的特征，我们设这些节点的特征组成一个N×D维的矩阵X，然后各个节点之间的关系也会形成一个N×N维的矩阵A，称为邻接矩阵（adjacency matrix）。X和A便是我们模型的输入。

GCN也是一个神经网络层，它的层与层之间的传播方式是：

这个公式中：

A波浪=A+I，I是单位矩阵

D波浪是A波浪的度矩阵（degree matrix）

H是每一层的特征，对于输入层的话，H就是X

σ是非线性激活函数

先不用考虑为什么要这样去设计一个公式。我们现在只用知道：

这个部分是可以事先计算好的

所以对于不需要去了解数学原理、只想应用GCN来解决实际问题的人来说，你只用知道：哦，这个GCN设计了一个牛逼的公式，用这个公式就可以很好地提取图的特征，而一个神经元包含一个函数和一个激活函数，这个公式就代表是神经元里的函数。这就够了，毕竟不是什么事情都需要知道内部原理，这是根据需求决定的

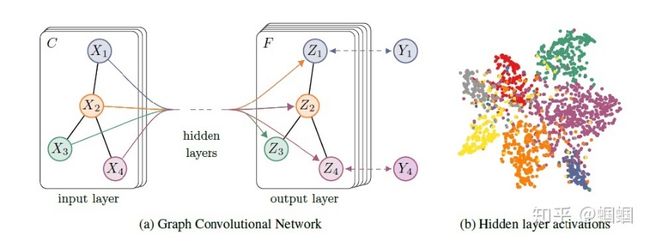
为了直观理解，我们用论文中的一幅图：

上图中的GCN输入一个图，通过若干层GCN每个node的特征从X变成了Z，但是，无论中间有多少层，node之间的连接关系，即A，都是共享的。

假设我们构造一个两层的GCN，激活函数分别采用ReLU和Softmax，则整体的正向传播的公式为下图所示，注意这里的应该是等于

最后，我们针对所有带标签的节点计算cross entropy损失函数：

四.GCN核心公式的由来

我们的每一层GCN的输入都是邻接矩阵A和node的特征H，那么我们直接做一个内积，再乘一个参数矩阵W，然后激活一下，就相当于一个简单的神经网络层嘛，是不是也可以呢？

实验证明，即使就这么简单的神经网络层，就已经很强大了。这个简单模型应该大家都能理解吧，这就是正常的神经网络操作。

但是这个简单模型有几个局限性：

1.只使用A的话，由于A的对角线上都是0，所以在和特征矩阵H相乘的时候，只会计算一个node的所有邻居的特征的加权和，该node自己的特征却被忽略了。因此，我们可以做一个小小的改动，给A加上一个单位矩阵I，这样就让对角线元素变成1了。

2.A是没有经过归一化的矩阵，这样与特征矩阵相乘会改变特征原本的分布，产生一些不可预测的问题。所以我们对A做一个标准化处理。首先让A的每一行加起来为1，我们可以乘以一个，D就是度矩阵。我们可以进一步把拆开与A相乘，得到一个对称且归一化的矩阵： 。

通过对上面两个局限的改进，我们便得到了最终的层特征传播公式：

其中=A+I,为的度矩阵（degree matrix）。

以上只是GCN的大致由来，更细节的地方可参考其他文章或论文。