CUBLAS 和 CUDNN

---

一、什么是CUBLAS

cuBLAS是BLAS的一个实现。BLAS是一个经典的线性代数库，他允许用户使用NVIDIA的GPU的计算资源。在使用cuBLAS的时候，应用程序应该分配矩阵或向量需要的GPU内存空间，并加载数据，调用所需要的cuBLAS函数，然后从GPU的内存空间上传计算结果到主机，cuBLAS API也提供了一些帮助函数来写或者从GPU中读取数据。

在使用cuBLAS的时候，cuBLAS使用的是列优先的数组，索引以1为基准。
相关头文件为 “cublas_v2.h”
其包含三类函数（向量标量，向量矩阵，矩阵矩阵）

CUBLAS实现矩阵乘法

cublasHandle_t handle;
cublasCreate(&handle);

//调用计算函数
cublasSgemm(handle, CUBLAS_OP_N, CUBLAS_OP_N, m, n, k, &alpha, *B, n, *A, k, &beta, *C, n);

//销毁句柄
cublasDestroy(handle);

…//回收计算结果，顺序可以和销毁句柄互换

CUBLAS中的Leading Dimension

在CUBLAS中，矩阵可以以行主序（row-major order）或列主序（column-major order）存储。了解leading dimension对于理解CUBLAS函数的参数传递和性能优化至关重要。

对于二维矩阵，leading dimension是矩阵的行数（row-major order）或列数（column-major order）。

列主序（column-major order，也称为Fortran顺序）：在这种顺序中，矩阵的列按连续内存地址存储。对于列主序矩阵，leading dimension是矩阵的行数。
例如，对于一个大小为MxN的列主序矩阵A，A(i, j)的内存位置可以通过以下计算得出：

location = i + j * M
其中i表示行索引，j表示列索引（从0开始）。

行主序（row-major order，也称为C顺序）：在这种顺序中，矩阵的行按连续内存地址存储。对于行主序矩阵，leading dimension是矩阵的列数。
例如，对于一个大小为MxN的行主序矩阵A，A(i, j)的内存位置可以通过以下计算得出：

location = i * N + j
其中i表示行索引，j表示列索引（从0开始）。

在使用CUBLAS函数时，需要指定leading dimension，以便库可以正确解释矩阵数据。例如，在CUBLAS的cublasDgemm函数中，用于矩阵乘法的参数lda、ldb和ldc分别表示输入矩阵A、B和输出矩阵C的leading dimensions。

在实践中，CUBLAS主要使用列主序（Fortran顺序）存储矩阵。在调用CUBLAS函数时，请确保矩阵以正确的顺序存储，并正确设置leading dimension。

CUBLAS LEVEL3函数 ： 矩阵矩阵

cublasStatus_t cublasSgemm(cublasHandle_t handle,
cublasOperation_t transa, cublasOperation_t transb,
int m, int n, int k,
const float *alpha, const float *A, int lda, const float *B, int ldb,
const float beta, floatC, int ldc) • 实现功能： C = alpha * op ( A ) * op ( B ) + beta * C
• 参数意义
• alpha和beta是标量， A B C是以列优先存储的矩阵
• 如果 transa的参数是CUBLAS_OP_N 则op(A) = A ，如果是CUBLAS_OP_T 则op(A)=A的转置
• 如果 transb的参数是CUBLAS_OP_N 则op(B) = B ，如果是CUBLAS_OP_T 则op(B)=B的转置
• Lda/Ldb:A/B的leading dimension，若转置按行优先，则leading dimension为A/B的列数
• Ldc：C的leading dimension，C矩阵一定按列优先，则leading dimension为C的行数

CUBLAS实现矩阵乘法

CUBLAS实现Batch版本矩阵乘法，如下图，最终结果是 [[c1,c2],[c3,c4]]矩阵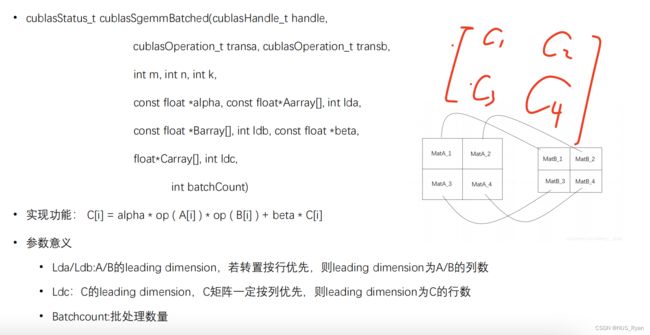

二、cuDNN

对于一些比较高级的算子，比如卷积算子，cudnn能够提供更加便捷的操作：
NVIDIA cuDNN是用于深度神经网络的GPU加速库。它强调性能、易用性和低内存开销
• NVIDIA cuDNN可以集成到更高级别的机器学习框架中
• 常用神经网络组件
• 常用语前向后向卷积网络
• 前像后向pooling
• 前向后向softmax
• 前向后向神经元激活
• Rectified linear (ReLU)、Hyperbolic tangent (TANH)
• Tensor transformation functions
• LRN, LCN and batch normalization forward and backward
• 头文件 include "cudnn.h“
• 学习网站： https://docs.nvidia.com/deeplearning/cudnn/

使用CuDNN实现卷积神经网络

创建cuDNN句柄
• cudnnStatus_t cudnnCreate(cudnnHandle_t *handle)

以Host方式调用在Device上运行的函数
• 比如卷积运算：cudnnConvolutionForward等

释放cuDNN句柄
• cudnnStatus_t cudnnDestroy(cudnnHandle_t handle)

将CUDA流设置&返回成cudnn句柄
• cudnnStatus_t cudnnSetStream(cudnnHandle_t handle, cudaStream_t streamId)
• cudnnStatus_t cudnnGetStream(cudnnHandle_t handle, cudaStream_t *streamId)

除此之外，cudnn还可以很方便地实现RNN，Softmax,Batch Normalization, ReLU, Sigmoid，Layer Normalization等等

四、CUBLAS和CUDNN实践

使用CUBLAS实现矩阵乘法：

#include
#include "cublas_v2.h"
#include "cuda_runtime.h"
#include "device_launch_parameters.h" 
using namespace std;
void checkResult(vector<double> h_C,vector<double> h_C_cpu){
  double epsilon = 5;
  bool match = 1;
  for(size_t i = 0;i < h_C.size();i++){
    if(abs(h_C[i] - h_C_cpu[i]) > epsilon){
      match = 0;
      cout<<"Arrays do not match!"<<endl;
      cout<<"h_C["<<i<<"] = "<<h_C[i]<<", h_C_cpu["<<i<<"] = "<<h_C_cpu[i]<<endl;
      break;
    }
  }
  if(match) cout<<"Arrays match."<<endl;
}
vector<double> matrixMulOnHost(vector<double> &A,vector<double> &B,int n){
  vector<double> C(n * n);
  for(size_t i = 0;i < n;i++){
    for(size_t j = 0;j < n;j++){
      double sum = 0;
      for(size_t k = 0;k < n;k++){
        double a = A[i + k * n];
        double b = B[k + n * j];
        sum += a * b;
      }
      C[i + n * j] = sum;
    }
  }
  return C;
}
int main(int argc,char *argv[]){
    int n = atoi(argv[1]);
    vector<double> h_A(n * n);
    vector<double> h_B(n * n);
    for(size_t i = 0;i< n ;i++){
      for(size_t j = 0; j < n ; j++){
      h_A[i + j * n] = static_cast<double>(rand()) / 100;
      h_B[i + j * n] = static_cast<double>(rand()) / 100;
    }
    }

    //Allocate Device Memory for matrix A and B and C 
    double *d_A,*d_B,*d_C; 
    cudaMalloc(&d_A,n * n * sizeof(double));
    cudaMalloc(&d_B,n * n * sizeof(double));
    cudaMalloc(&d_C,n * n * sizeof(double)); 


    
    //copy matrix A and B from host to the device 
    cudaMemcpy(d_A,h_A.data(),n * n * sizeof(double),cudaMemcpyHostToDevice);
    cudaMemcpy(d_B,h_B.data(),n * n * sizeof(double),cudaMemcpyHostToDevice); 

    //Create a CUBLAS handle 
    cublasHandle_t handle; 
    cublasCreate(&handle); 

    //Setup alpha and beta 
    double alpha = 1.0;
    double beta = 0.0; 


    cudaEvent_t start,stop;
    cudaEventCreate(&start);
    cudaEventCreate(&stop);
    cudaEventRecord(start,0);
    //Perform matrix multiplication (d_C = alpha * d_A * d_B + beta * d_C) using CUBLAS 
    //d_A : [m,k], d_B : [k,n], d_C : [m,n]
    cublasDgemm(
      handle,
      CUBLAS_OP_N, // No Transition
      CUBLAS_OP_N, // No Transition
      n, // m
      n, // n
      n, // k
      &alpha, // alpha 
      d_A, // d_A
      n, // lda 
      d_B, // d_B
      n, // ldb
      &beta, // beta
      d_C, // d_C
      n // ldc
    );
    
    //Allocate host memory for the result matrix C and copy it from device to host memory 
    
    cudaEventRecord(stop,0);
    cudaEventSynchronize(stop);
    float elapsedTime;
    cudaEventElapsedTime(&elapsedTime,start,stop);
    cout<<"Time taken for matrix multiplication of "<<n<<" * "<<n<<" matrix is "<<elapsedTime<<" ms"<<endl;

    vector<double> h_C(n * n); 
    cudaMemcpy(h_C.data(),d_C,n * n * sizeof(double),cudaMemcpyDeviceToHost); 
    vector<double> h_C_host = matrixMulOnHost(h_A,h_B,n);
    checkResult(h_C,h_C_host);
    //Free device memory 
    cudaFree(d_A);
    cudaFree(d_B);
    cudaFree(d_C);

    //Destroy the CUBLAS handle 
    cublasDestroy(handle);
    return 0;

}

这段代码的运行结果是:
Time taken for matrix multiplication of 1024 * 1024 matrix is 5.38173 ms

---