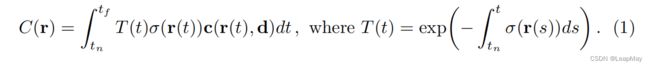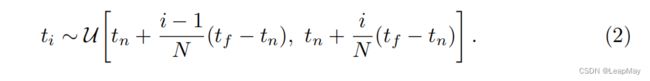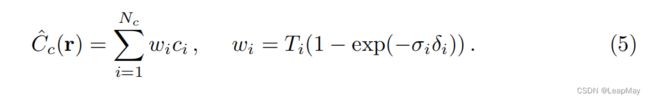NeRF开山之作一：NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis 论文解读与公式推导（二）

接上文

NeRF开山之石：NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis 论文解读与公式推导（一）_LeapMay的博客-CSDN博客

本文提出了一种名为NeRF（Neural Radiance Fields）的方法，用于将场景表示为神经辐射场以进行视图合成。传统的方法使用离散的表面几何或体素表示来建模场景，但这些方法无法捕捉到真实场景的细节和光照效果。相反，NeRF利用深度神经网络来表示场景中每个点的辐射强度和颜色。具体而言，NeRF通过在相机光线上均匀采样点，并通过神经网络估计每个采样点的辐射强度和颜色。然后，通过卷积积分计算出相机光线通过场景的颜色。通过训练网络来最小化合成图像与真实图像之间的差异，可以学习到准确的场景表示。实验证明，NeRF能够生成高质量的合成图像，并且对于复杂的场景和光照效果具有较强的泛化能力。NeRF为视图合成任务提供了一种新的建模和渲染方法，并为深度学习在计算机图形学中的应用开辟了新的方向。 

 

3 Neural Radiance Field Scene Representation（神经辐射场场景表征）

We represent a continuous scene as a 5D vector-valued function whose input is a 3D location x = ( x, y, z ) and 2D viewing direction ( θ, φ), and whose output is an emitted color c = ( r, g, b ) and volume density σ . In practice, we express direction as a 3D Cartesian unit vector d. We approximate this continuous 5D  scene representation with an MLP network F Θ : ( x , d ) → ( c, σ) and optimize its weights Θ to map from each input 5D coordinate to its corresponding volume density and directional emitted color.

We encourage the representation to be multiview consistent by restricting the network to predict the volume density σ as a function of only the location x , while allowing the RGB color c to be predicted as a function of both location and viewing direction. To accomplish this, the MLP F Θ fifirst processes the input 3D coordinate x with 8 fully-connected layers (using ReLU activations and 256 channels per layer), and outputs σ and a 256-dimensional feature vector. This feature vector is then concatenated with the camera ray’s viewing direction and passed to one additional fully-connected layer (using a ReLU activation and 128 channels) that output the view-dependent RGB color.

我们将连续场景表示为一个5维向量值函数，其输入是3D位置x=(x, y, z)和2D观察方向(θ, φ)，输出是发射颜色c=(r, g, b)和体密度σ。在实践中，我们将方向表示为一个3D笛卡尔单位向量d。我们使用一个MLP网络FΘ：(x, d) → (c, σ)来近似这个连续的5维场景表示，并优化其权重Θ，将每个输入的5维坐标映射到对应的体密度和方向性发射颜色。

为了确保多视角的一致性，我们限制网络仅根据位置x预测体密度σ，而允许RGB颜色c根据位置和观察方向进行预测。为了实现这一点，MLP FΘ首先使用8个全连接层（每层使用ReLU激活函数和256个通道）处理输入的3D坐标x，并输出σ和一个256维的特征向量。然后，将该特征向量与相机射线的观察方向串联起来，并通过一个额外的全连接层（使用ReLU激活函数和128个通道）输出与观察方向相关的RGB颜色。

 其中MLP表示多层感知器（Multilayer Perceptron），ReLU表示整流线性单元（Rectified Linear Unit）。该方法通过将位置和观察方向作为输入，并使用MLP网络来近似表示连续场景，以实现对体密度和方向性发射颜色的预测。同时，通过限制体密度的预测仅与位置有关，而允许RGB颜色的预测与位置和观察方向相关，来确保多视角一致性。

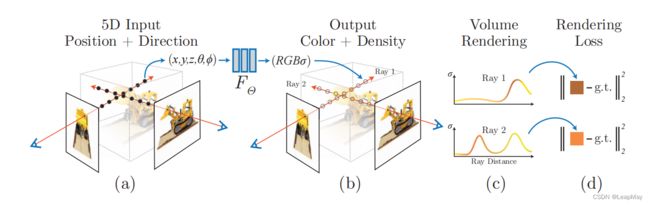
Fig. 2: An overview of our neural radiance fifield scene representation and diffffer entiable rendering procedure. We synthesize images by sampling 5D coordinates  (location and viewing direction) along camera rays (a), feeding those locations into an MLP to produce a color and volume density (b), and using volume rendering techniques to composite these values into an image (c). This rendering function is difffferentiable, so we can optimize our scene representation by minimizing the residual between synthesized and ground truth observed images (d).

图2：神经辐射场场景表示和可微分渲染过程的概览。通过沿着相机射线采样5D坐标（位置和观察方向）来合成图像（a），将这些位置输入到MLP中以生成颜色和体密度（b），并使用体渲染技术将这些值合成为图像（c）。这个渲染函数是可微分的，因此可以通过最小化合成图像和真实观测图像之间的残差来优化我们的场景表示（d）。

Fig. 3: A visualization of view-dependent emitted radiance. Our neural radiance fifield representation outputs RGB color as a 5D function of both spatial position x and viewing direction d. Here, we visualize example directional color distributions for two spatial locations in our neural representation of the Ship scene. In (a) and (b), we show the appearance of two fifixed 3D points from two different camera positions: one on the side of the ship (orange insets) and one on the surface of the water (blue insets). Our method predicts the changing specular appearance of these two 3D points, and in (c) we show how this behavior generalizes continuously across the whole hemisphere of viewing directions.

 图3：视角相关的辐射亮度可视化。该文神经辐射场表示将RGB颜色作为关于空间位置x和观察方向d的5D函数输出。这里，我们展示了船舶场景中两个空间位置在神经表示中的方向颜色分布。在（a）和（b）中，我们展示了两个不同相机位置的两个固定的3D点的外观：一个在船的侧面（橙色插图），一个在水面上（蓝色插图）。我们的方法预测了这两个3D点的变化的镜面反射外观，在（c）中我们展示了这种行为在整个观察方向半球上的连续性泛化。图3展示了我们的方法如何利用输入的观察方向来表示非兰伯特效应的示例。

4 Volume Rendering with Radiance Fields（基于辐射场进行体积渲染）

5D神经辐射场将场景表示为空间中任意点的体积密度和方向性辐射。我们使用经典体积渲染原理[16]来渲染通过场景的任意光线的颜色。体积密度σ(x)可以解释为光线在位置x处终止于无穷小粒子的微分概率。相机光线r(t) = o + td（其中o是起始点，d是方向向量，t是光线长度）的预期颜色C(r)在近和远边界tn和tf之间计算如下：

 函数T(t)表示光线从tn到t的累积透射率，即光线在从tn到t的路径上未碰撞到其他粒子的概率。从我们连续的神经辐射场渲染视图需要对通过所需虚拟相机的每个像素跟踪的相机光线估计这个积分C(r)。

我们使用数值积分方法对这个连续积分进行估计。通常用于渲染离散化体素网格的确定性积分会有效地限制我们表示的分辨率，因为MLP仅在固定的离散位置查询。相反，我们采用分层抽样方法，将[tn, tf]划分为N个均匀间隔的区间，然后在每个区间内均匀随机抽取一个样本：

 尽管我们使用离散的样本集来估计积分，但分层抽样使我们能够表示连续的场景，因为它导致MLP在优化过程中在连续位置上进行评估。我们使用这些样本使用Max在体积渲染综述中讨论的积分规则来估计C(r)。

 

 其中δi = ti+1 - ti是相邻样本之间的距离。从（ci，σi）值集合计算Cˆ(r)的函数是可微的，并且可以简化为使用α值进行传统的alpha合成，其中αi = 1 - exp（-σiδi）。

5 Optimizing a Neural Radiance Field（优化神经辐射场）

在前面的部分中，我们描述了将场景建模为神经辐射场并从该表示中渲染新视角所需的核心组件。然而，我们观察到这些组件还不足以实现最先进的质量，如第6.4节所示。为了实现对高分辨率复杂场景的表示，我们引入了两项改进。第一项改进是对输入坐标进行位置编码，以帮助MLP表示高频函数。第二项改进是采用分层采样过程，以便高效地对这种高频表示进行采样。

5.1 Positional encoding

 在神经网络被认为是通用函数逼近器的前提下 [14]，我们发现直接让网络 FΘ 在 xyzθφ 的输入坐标上操作会导致渲染效果较差，无法有效表示颜色和几何形状的高频变化。这与Rahaman等人最近的研究结果相一致 [35]，他们表明深度网络更倾向于学习低频函数。他们还指出，将输入通过高频函数映射到更高维度的空间中，然后再传递给网络，可以更好地拟合包含高频变化的数据。我们在神经场景表示的背景下利用了这些发现，并展示了将 FΘ 重新表述为两个函数的组合 FΘ = F 0Θ ◦ γ，其中一个函数是可学习的，另一个函数则不是，可以显著提高性能（参见图4和表2）。这里的 γ 是从 R 映射到更高维度空间 R 2L 的函数，而 F 0Θ 仍然是一个常规的 MLP。具体地，我们使用的编码函数为：

该函数γ(·)分别应用于x中的三个坐标值（归一化为[-1, 1]区间）以及笛卡尔视线方向单位向量d的三个分量（根据构造，它们在[-1, 1]区间内）。 在我们的实验中，我们设置γ(x)的L值为10，γ(d)的L值为4。 类似的映射在流行的Transformer架构中也被使用，其中被称为位置编码。

然而，Transformer将其用于将序列中的离散位置标记作为输入提供给不包含任何顺序概念的架构。相比之下，我们使用这些函数将连续的输入坐标映射到更高维度的空间，使得我们的MLP能够更容易地逼近高频函数。 与此同时，与解决从投影中建模3D蛋白质结构的相关问题的并行工作[51]也使用了类似的输入坐标映射方法。 

5.2 Hierarchical volume sampling 

我们的渲染策略是在每条相机射线上密集地评估神经辐射场网络的N个查询点，这是低效的：不会对渲染图像产生贡献的自由空间和被遮挡的区域仍然被重复采样。我们从体积渲染的早期工作[20]中汲取灵感，并提出一种层次化表示方法，通过根据对最终渲染的预期影响来分配样本，从而提高渲染效率。

我们不仅使用一个网络来表示场景，而是同时优化两个网络：一个“粗糙”的网络和一个“精细”的网络。我们首先使用分层采样方法对一组Nc个位置进行采样，并根据第2和第3个等式在这些位置上评估“粗糙”网络。给定“粗糙”网络的输出，我们可以对沿着每条射线的点进行更具信息的采样，其中样本偏向于体积的相关部分。为了做到这一点，我们首先将第3个等式中来自粗糙网络的alpha混合颜色Cˆc(r)重新写为沿着射线的所有采样颜色ci的加权和：

 将这些权重标准化为ˆ，沿着射线产生了分段常数的概率密度函数（PDF）。我们使用逆变换采样从这个分布中采样第二组Nf个位置，在第一组和第二组样本的并集上评估我们的“精细”网络，并使用第3个等式计算射线的最终渲染颜色Cˆf(r)，但使用所有的Nc+Nf个样本。这个过程将更多的样本分配给我们预期包含可见内容的区域。这解决了重要性采样的类似目标，但我们将采样值用作整个积分域的非均匀离散化，而不是将每个样本视为整个积分的独立概率估计。

 5.3 Implementation details

 对于每个场景，我们针对其优化一个单独的神经连续体表示网络。这只需要场景的一组捕获的RGB图像、相应的相机姿态和内参参数以及场景边界（对于合成数据，我们使用真实的相机姿态、内参和边界，对于真实数据，我们使用COLMAP结构运动估计包[39]来估计这些参数）。在每次优化迭代中，我们从数据集的所有像素中随机采样一个相机射线批次，然后按照第5.2节中描述的分层采样方法，从粗糙网络中查询Nc个样本和从精细网络中查询Nc + Nf个样本。然后，我们使用第4节中描述的体素渲染过程为两组样本中的每条射线渲染颜色。我们的损失函数就是粗糙渲染和精细渲染的渲染像素颜色与真实像素颜色之间的总平方误差。

其中，R是每个批次中的射线集合，C(r)、Cˆ c(r)和Cˆ f(r)分别是射线r的真实颜色、粗糙体积预测颜色和精细体积预测颜色。请注意，尽管最终渲染来自Cˆ f(r)，但我们也最小化了Cˆ c(r)的损失，以便可以使用粗糙网络中的权重分布来分配精细网络中的样本。

在我们的实验中，我们使用了批量大小为4096个射线，每个射线在粗糙体积中采样Nc = 64个坐标，在精细体积中采样额外的Nf = 128个坐标。我们使用Adam优化器[18]，学习率从5 × 10^-4开始指数衰减到5 × 10^-5（其他Adam超参数保持默认值，即β1 = 0.9、β2 = 0.999和 = 10^-7）。针对单个场景的优化通常需要大约100-300k次迭代才能在一张NVIDIA V100 GPU上收敛（约1-2天的时间）。

6 Results

我们在定量上（表1）和定性上（图8和图6）展示了我们的方法优于先前的工作，并提供了大量的消融研究来验证我们的设计选择（表2）。我们鼓励读者观看我们的补充视频，以更好地了解我们的方法在渲染平滑路径的新视图时相对于基准方法的显著改进。

 7 Conclusion

本文直接解决了先前使用MLP表示对象和场景作为连续函数的方法的不足之处。我们证明将场景表示为5D神经辐射场（一种根据3D位置和2D视角方向输出体密度和视角相关辐射的MLP）比先前主导的使用深度卷积网络训练输出离散化体素表示的方法产生更好的渲染效果。尽管我们提出了一种分层采样策略以使渲染更具样本效率（用于训练和测试），但在有效优化和渲染神经辐射场方面仍有许多进展空间。未来的工作方向之一是可解释性：例如，体素网格和网格等采样表示可以对渲染视图的预期质量和失败模式进行推理，但是当我们将场景编码为深度神经网络的权重时，如何分析这些问题尚不清楚。我们相信，这项工作在基于真实世界图像的图形管道方面取得了进展，复杂场景可以由从实际对象和场景图像中优化得到的神经辐射场组成。