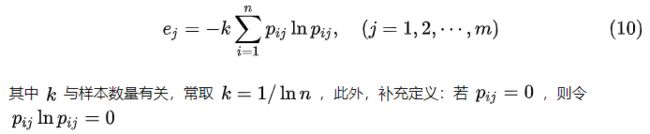TOPSIS法(优劣解距离法)介绍及 python3 实现
本文转载自博文: TOPSIS法(优劣解距离法)介绍及 python3 实现
这里也给出一个很好的参考资料:夹逼对抗解释结构模型(SAISM)即TOPSIS-AISM联用模型
文章目录
-
-
-
- 1. 简述
- 2. TOPSIS过程
-
- 2.1 指标属性同向化
-
- 2.1.1 极小型指标
- 2.1.2 中间型指标
- 2.1.3 区间型指标
- 2.2 构造归一化初始矩阵
- 2.3 确定最优方案和最劣方案
- 2.4 计算各评价对象与最优/劣方案的接近程度
- 2.5 计算各评价对象与 最劣方案 的距离 C i C_i Ci
- 2.6 根据 C i C_i Ci 大小进行排序,给出评价结果
- 2.7 TOPSIS法算法程序
- 3. 案例及程序调用实例
-
- 3.1 问题提出
- 3.2 指标同向化处理
- 3.3 构造归一化初始矩阵
- 3.4 确定最优方案和最劣方案
- 3.5 计算得分,进行排序
- 3.6 雷达图分析
- 3.7 实现代码
- 4. 合理确定指标权重是 TOPSIS 综合评价的关键
-
- 4.1 基于信息论的熵值法(数据差异程度)
-
- 4.1.1 熵值法过程
- 4.1.2 结果分析
- 4.1.3 熵值法实现代码
-
-
1. 简述
C.L.Hwang 和 K.Yoon 于1981年首次提出 TOPSIS (Technique for Order Preference by Similarity to an Ideal Solution)。TOPSIS 法是一种常用的组内综合评价方法,能充分利用原始数据的信息,其结果能精确地反映各评价方案之间的差距。基本过程为基于归一化后的原始数据矩阵,采用余弦法找出有限方案中的最优方案和最劣方案,然后分别计算各评价对象与最优方案和最劣方案间的距离,获得各评价对象与最优方案的相对接近程度,以此作为评价优劣的依据。该方法对数据分布及样本含量没有严格限制,数据计算简单易行。
通俗的例子:小明数学考试 134 分,要怎么知道他的成绩是好还是不好呢?
基于分布的评价方法会观察小明的分数位于班级分数的哪个水平(如前 5%、前 10%),但这种评价方法只能给出一个方向的情况。如班上成绩除了最高分外,其余都是 134 分,那么小明的成绩就是并列的倒数第一,但是正向评价给出的结果是前 5%。
而 TOPSIS 就是找出班上最高分(假设是 147 分)、最低分(假设是 69 分),然后计算小明的分数和这两个分数之间的差距,从而得到自己分数好坏的一个客观评价。距离最高分越近,那么评价情况越好,距离最低分越近,那么评价情况越糟。
2. TOPSIS过程
网上大部分资料对此部分均有描述,但不少资料与文献原文存在较大偏差、排版较为混乱,并且没有深入思考原理。此部分内容转述外网文献,并加入了笔者自己的理解。

2.1 指标属性同向化
TOPSIS 法使用距离尺度来度量样本差距,使用距离尺度就需要对指标属性进行同向化处理(若一个维度的数据越大越好,另一个维度的数据越小越好,会造成尺度混乱)。通常采用成本型指标向效益型指标转化(即数值越大评价越高,事实上几乎所有的评价方法都需要进行转化),此外,如果需要使用雷达图进行展示,建议此处将所有数据都变成正数。
2.1.1 极小型指标
M M M 为指标 x x x 可能取值的最大值。
2.1.2 中间型指标
中间型指标:期望指标值既不要太大也不要太小,适当取中间值最好(如水质量评估 PH 值)
其中 M M M 为指标 x x x 的可能取值的最大值, m m m 为指标 x x x 的可能取值的最小值
2.1.3 区间型指标
区间型指标:期望指标的取值最好落在某一个确定的区间最好(如体温)
其中 [ a , b ] [a, b] [a,b] 为指标 x x x 的最佳稳定区间, [ a ∗ , b ∗ ] [a^*, b^*] [a∗,b∗] 为最大容忍区间。
指标属性同向化实现代码:
def dataDirection_1(datas, offset=0):
def normalization(data):
return 1 / (data + offset)
return list(map(normalization, datas))
def dataDirection_2(datas, x_min, x_max):
def normalization(data):
if data <= x_min or data >= x_max:
return 0
elif data > x_min and data < (x_min + x_max) / 2:
return 2 * (data - x_min) / (x_max - x_min)
elif data < x_max and data >= (x_min + x_max) / 2:
return 2 * (x_max - data) / (x_max - x_min)
return list(map(normalization, datas))
def dataDirection_3(datas, x_min, x_max, x_minimum, x_maximum):
def normalization(data):
if data >= x_min and data <= x_max:
return 1
elif data <= x_minimum or data >= x_maximum:
return 0
elif data > x_max and data < x_maximum:
return 1 - (data - x_max) / (x_maximum - x_max)
elif data < x_min and data > x_minimum:
return 1 - (x_min - data) / (x_min - x_minimum)
return list(map(normalization, datas))
2.2 构造归一化初始矩阵
设共有 n n n 个待评价对象,每个对象都有 m m m 个指标(属性),则原始数据矩阵构造为:

构造加权规范矩阵,属性进行向量规范化,即每一列元素都除以当前列向量的范数(使用余弦距离度量):

由此得到归一化处理后的标准化矩阵 Z Z Z :

2.3 确定最优方案和最劣方案
最优方案 Z + Z^+ Z+ 由 Z Z Z 中每列元素的最大值构成:
![]()
最劣方案 Z − Z^- Z− 由 Z Z Z 中每列元素的最小值构成:
![]()
2.4 计算各评价对象与最优/劣方案的接近程度

其中 W j W_j Wj 为第 j j j 个属性的权重(重要程度),指标权重建议根据实际确定或使用专家评估方法。基于信息论的 熵值法 和 (AHP)层次分析法 ,在本文第 4 部分也提供了方法的简要介绍。
2.5 计算各评价对象与 最劣方案 的距离 C i C_i Ci
- 上式分子为 D i − {D^-_i} Di−, 计算的是各评价对象与 最劣方案 的距离 (即与最优方案的贴近程度)。 0 ≤ C i ≤ 1 , C i → 1 0 \le {C_i} \le 1,{\kern 1pt} {\kern 1pt}{C_i} \to 1 0≤Ci≤1,Ci→1 表明评价对象越优 (距离最劣方案越远, 则方案越优)。
- 此处也可以将分子设置为 D i + {D^+_i} Di+, 表示与 最优方案 的距离 (即与最劣方案的贴近程度), 此时 0 ≤ C i ≤ 1 , C i → 0 0 \le {C_i} \le 1,{\kern 1pt} {\kern 1pt}{C_i} \to 0 0≤Ci≤1,Ci→0 表明评价对象越优 (距离最优方案越近, 则方案越优)。
2.6 根据 C i C_i Ci 大小进行排序,给出评价结果
2.7 TOPSIS法算法程序
使用的编程语言:python3.7.1 (Anaconda3)
使用的编辑器:Sublime Text 3
使用的模块:pandas、numpy
import pandas as pd
import numpy as np
def topsis(data, weight=None):
# 归一化
data = data / np.sqrt((data ** 2).sum())
# 最优最劣方案
Z = pd.DataFrame([data.min(), data.max()], index=['负理想解', '正理想解'])
# 熵权法计算权值
weight = get_entropy_weight_1(data) if weight is None else np.array(weight)
Result = data.copy()
# 计算距离
Result['正理想解'] = np.sqrt(((data - Z.loc['正理想解']) ** 2 * weight).sum(axis=1))
Result['负理想解'] = np.sqrt(((data - Z.loc['负理想解']) ** 2 * weight).sum(axis=1))
# 综合得分指数
Result['综合得分指数'] = Result['负理想解'] / (Result['负理想解'] + Result['正理想解'])
Result['排序'] = Result.rank(ascending=False)['综合得分指数']
return Result, Z, weight
topsis 函数需要输入:
- data:原始数据,pandas.DataFrame 类型
- weight:权系数, 默认使用熵权法定权. 也可以传入指定权重列表. (熵权法代码见下文)
3. 案例及程序调用实例
3.1 问题提出
为了客观地评价我国研究生教育的实际状况和各研究生院的教学质量,国务院学位委员会办公室组织过一次研究生院的评估。为了取得经验,先选5所研究生院,收集有关数据资料进行了试评估,下表是所给出的部分数据:

3.2 指标同向化处理
3.3 构造归一化初始矩阵
3.4 确定最优方案和最劣方案
3.5 计算得分,进行排序
计算各评价对象与最优方案的接近程度及最终得分,并进行排序。
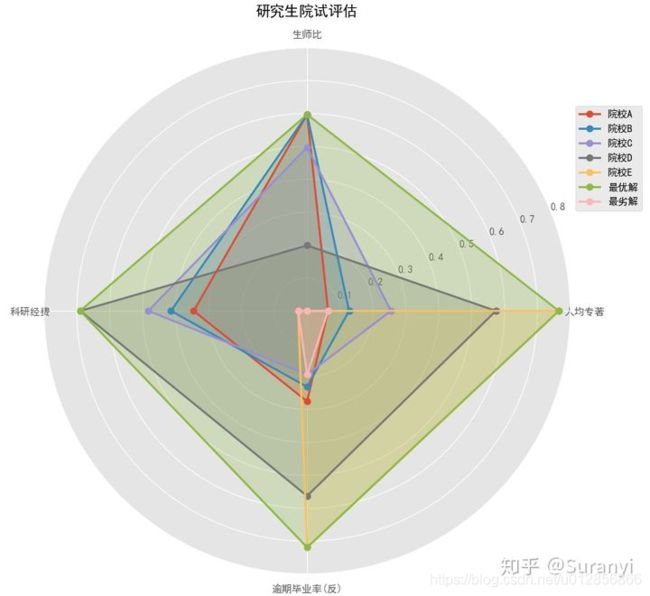
3.6 雷达图分析
3.7 实现代码
import pandas as pd
def dataDirection_3(datas, x_min, x_max, x_minimum, x_maximum):
def normalization(data):
if data >= x_min and data <= x_max:
return 1
elif data <= x_minimum or data >= x_maximum:
return 0
elif data > x_max and data < x_maximum:
return 1 - (data - x_max) / (x_maximum - x_max)
elif data < x_min and data > x_minimum:
return 1 - (x_min - data) / (x_min - x_minimum)
return list(map(normalization, datas))
data = pd.DataFrame(
{'人均专著': [0.1, 0.2, 0.4, 0.9, 1.2], '生师比': [5, 6, 7, 10, 2], '科研经费': [5000, 6000, 7000, 10000, 400],
'逾期毕业率': [4.7, 5.6, 6.7, 2.3, 1.8]}, index=['院校' + i for i in list('ABCDE')])
data['生师比'] = dataDirection_3(data['生师比'], 5, 6, 2, 12) # 师生比数据为区间型指标
data['逾期毕业率'] = 1 / data['逾期毕业率'] # 逾期毕业率为极小型指标
out = topsis(data, weight=[0.2, 0.3, 0.4, 0.1]) # 设置权系数
4. 合理确定指标权重是 TOPSIS 综合评价的关键
权重计算的确定方法在综合评价中重中之重,不同的方法对应的计算原理并不相同。
通常来说采用TOPSIS方法采用的是客观法,因为客观法可以利用当前的数据直接求出权重,计算上非常方便。常见的客观赋权法如下:
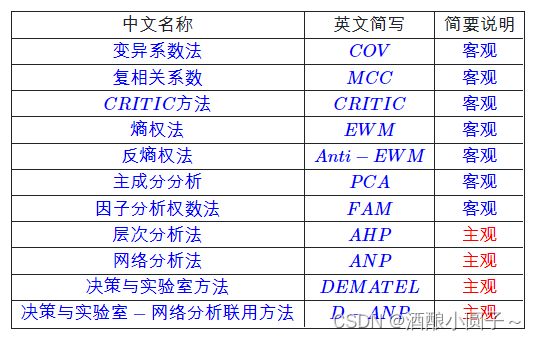
这里重点介绍熵权法(EWM),其他几种方法可以参考:http://www.huaxuejia.cn/ism/CESAISM/topsis_saism.php
4.1 基于信息论的熵值法(数据差异程度)
4.1.1 熵值法过程
基于信息论的熵值法是根据各指标所含信息有序程度的差异性来确定指标权重的客观赋权方法,仅依赖于数据本身的离散程度。
熵用于度量不确定性,指标的离散程度越大(不确定性越大)则熵值越大,表明指标值提供的信息量越多,则该指标的权重也应越大。主要计算步骤如下:
Step1: 对原始数据矩阵 (4) 按列进行归一化处理
注意:
- 这里不能是同向化后的矩阵,会损失原始信息
- 归一化方法不唯一,可使用min-max归一化,mean-std归一化或者向量归一化等。
Step3: 计算各指标的权系数:
![]()
熵权系数 h j h_j hj 越大,则该指标代表的信息量越大,表示其对综合评价的作用越大。
4.1.2 结果分析
上面的方法看着很高大上,但是直觉告诉我(们),从数据推出的权重,往往都不具有现实意义。那这个到底是什么意思呢?我们用第 3 部分的数据测试一下:
-
各指标的熵值和权系数为:

发现了吗?熵值、权系数、方差间的大小次序是相关的,如果对熵的概念较为陌生,那不妨换个角度想想:什么类型的数据会导致方差小?如人体体温变化,体温的变化都是在一个微小的范围内,这样就造成了这一属性的变异程度较小,使用熵权法(主成分分析法同理)进行计算时,获得的权系数较小,变得 “不那么重要”。但事实上即使构造了合理的权系数,在对数据做变换(如成本型指标取倒数),这种权系数的设置是否仍然合理都是个问题(数据分布情况发生了改变)。
一种减轻这种影响的方法是选择更合理的归一化方法去除指标的量纲。如变化范围较大的数据可以使用小数定标规范化、正态分布的数据使用 z 分数变换、均匀分布的数据使用离差标准化。通过这种方法,可以获得较为 “合理” 的指标权。但要注意的是合不合理都是相对的,事实上许多文献没有考虑到这种方法背后的意义,但其计算得到的结论很实用(滑动权值经验模式,未来在介绍其他评价方法时再做详细介绍),即衡量模型的优劣并不是看系数合不合理,而是效果好不好/符不符合实际。
结论:评价结果、评价方法的好坏,本身就具有很强的主观性。马克思主义告诉我们“具体问题具体分析。在矛盾普遍性原理的指导下,具体分析矛盾的特殊性,并找出解决矛盾的正确方法。”。怎么在论文中将你的思想、选取方法的原则、指标选取、权重构造尽可能详尽的展示,才是方法应用成功与否的关键。
4.1.3 熵值法实现代码
先定义基础数据:
data = pd.DataFrame(
{'人均专著': [0.1, 0.2, 0.4, 0.9, 1.2], '生师比': [5, 6, 7, 10, 2], '科研经费': [5000, 6000, 7000, 10000, 400],
'逾期毕业率': [4.7, 5.6, 6.7, 2.3, 1.8]}, index=['院校' + i for i in list('ABCDE')])
【实现代码 1】:
import numpy as np
def get_entropy_weight_1(data): # 熵权法需要使用原始数据作为输入
data = np.array(data)
# 数据归一化
# 这里可以根据需要选择mean-std归一化或者min-max归一化
# 计算Pij
P = data / data.sum(axis=0) # 需要考虑分子为0的情况,可以考虑加一个epsilon=1e-3
# 计算熵值
E = np.nansum(-P * np.log(P) / np.log(len(data)), axis=0)
# 计算权系数
return (1 - E) / (1 - E).sum()
get_entropy_weight_1(data)
程序输出结果:
array([ 0.41803075, 0.14492264, 0.28588943, 0.15115718])
【实现代码 2】:
def get_entropy_weight_2(data):
"""
:param data: dataframe类型
:return: 各指标权重列表
"""
# 数据归一化
# 这里可以根据需要选择mean-std归一化或者min-max归一化
m,n=data.shape
#将dataframe格式转化为matrix格式
data=data.as_matrix(columns=None)
# 第一步:计算k
k=1/np.log(m)
#第二步:计算pij
pij=data/data.sum(axis=0)
# 第三步:计算每种指标的信息熵
tmp=np.nan_to_num(pij*np.log(pij))
ej=-k*(tmp.sum(axis=0))
# 第四步:计算每种指标的权重
wi=(1-ej)/np.sum(1-ej)
wi_list=list(wi)
return wi_list
get_entropy_weight_2(data)
[0.41803075156086411,
0.14492263660659988,
0.28588943395852595,
0.15115717787401006]
可以看到,两个代码的输出结果一致,且各个属性的权值加起来和为1。
这里,有几个需要注意的点:
- 数据归一化:在原始数据量纲不一致时,我们使用熵权法之前可以先对数据做归一化处理。这里可以根据数据的实际情况和业务需要选择mean-std归一化或者min-max归一化。不同的归一化方法,对最后求出来的权值会有影响。
- 除数为0的情况:上述计算过程涉及除法,会遇到除数为0的情况。可以给除数加一个很小的数值,如epsilon=1e-3,以避免除以0的情况发生。

![[公式]](http://img.e-com-net.com/image/info8/5317c4e6b9d74a80b4bec87f74b60459.jpg)