2023数维杯A题水体污染对流弥散吸附完整论文及所有数值计算模拟代码
大家好呀,从昨天发布赛题一直到现在,总算完成了数维杯A题完整的成品论文。
A题论文37页,一些修改说明提醒7页,正文22页,附录8页
本论文可以保证原创,保证高质量。绝不是随便引用一大堆模型和代码复制粘贴进来完全没有应用糊弄人的垃圾半成品论文。
本次用MATLAB求解,肝了一个通宵代码,一直在做修改,是我近期比赛技术含量很高的一篇了,这个题小问虽然不多,但实际求解起来是很麻烦的,要注意的是,这道题不是数据驱动,一切要从内部机理的理论模型出发,这个是需要查阅文献的,但理论模型不止一个,我们要根据实际求解过程为导向。确定完理论模型其实就是数值模拟求解理论模型里面的参数了,第二问我先是用后面两个表格分别用代码数值计算出了吸附速率常数和等温线模型参数,结合对流弥散参数表就能进行数值模拟了,我给了一个三维浓度分布图。第三问还是一样,先确定降解的内部机理理论,之后根据数据数值计算理论模型的参数即可。
实在精力有限,没力气打太多字做文字版讲解了,可能讲得不够详细,可以看我的视频讲解:
2023数维杯数学建模A题水体污染保姆级手把手教学!(结尾为B题说明)_哔哩哔哩_bilibili
OK,这里是我的
目录:
摘要:
第一问:
记住,重点是要有分析过程,也就是推导过程。
此外,理论模型必须要能结合问题二的参数和数据表!也就是说,建立的这个理论模型,最起码应该能够结合这些参数:
此外还必须涉及吸附动力学模型和等温平衡吸附模型。
基于这样的考虑,我们分别推导建立对流、弥散和吸附模型:
推导之后汇总一起就是最终的理论模型框架了。
第二问:
首先确定研究思路,根据表2表3数值计算拟合出理论模型的参数,之后再结合表1这个给定的参数,就可以进行实际的数值模拟。
大家一定要注意,我们要分析的是“机理”
所以,必须是先确定一个涉及内部机理的理论方程,之后对于这个理论方程中不确定的参数进行数值计算。
而不是通过数据直接拟合出一个方程,这两者从底层逻辑上是完全不同的。
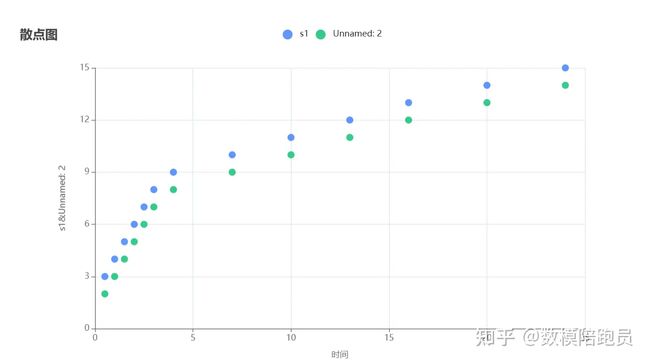
如果是直接拟合:
过这几个散点可以有很多种不同的拟合函数。
但每个函数每一项的系数的物理含义是什么?这个我们是不知道的
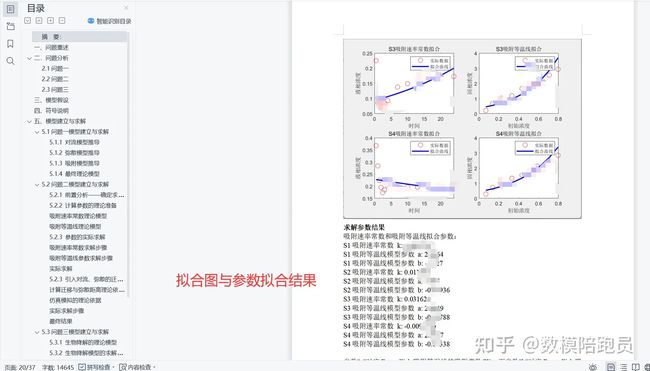
所以必须要先分析机理:
之后实际求解:
这每一个参数可都是有实际的物理含义的,例如吸附的速度
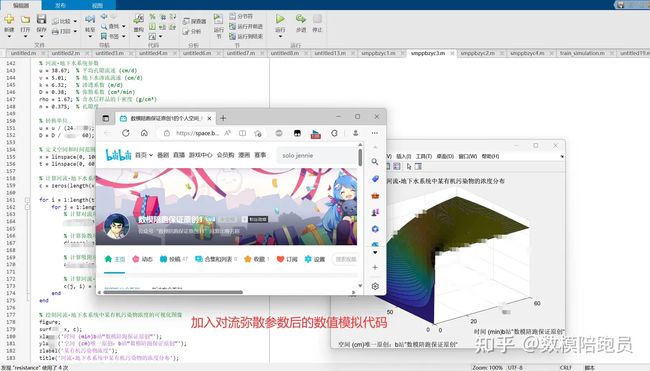
加下来模拟:
这里我模拟了两个结果:
1.给出了任意特定时间内的迁移和弥散距离:
2.给出了一个三维模型,可以给出空间内任意一点任意时间的污染物浓度:
OK第二问结束。
第三问:
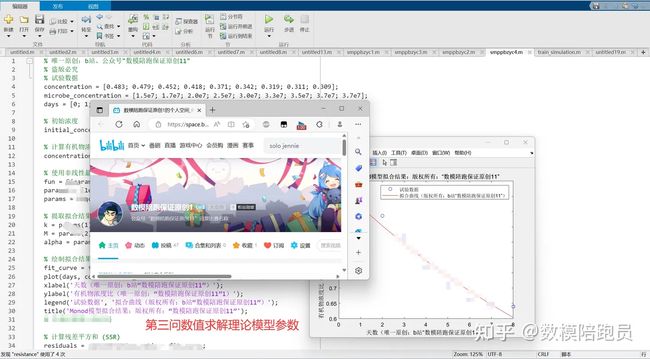
一样的流程啦,先引入内部机理的理论模型:
之后实际求解:
OK以上就是论文部分啦,为保证限量,我只粘贴导入数据部分的代码吧:
% 第二个表格数据
time = [0.5, 1, 1.5, 2, 2.5, 3, 4, 7, 10, 13, 16, 20, 24]; % 时间
liquid_s1 = [0.355, 0.312, 0.305, 0.31, 0.314, 0.325, 0.353, 0.36, 0.359, 0.362, 0.371, 0.365, 0.364]; % S1液相浓度
solid_s1 = [2.3, 2.73, 2.8, 2.75, 2.71, 2.6, 2.32, 2.25, 2.26, 2.23, 2.14, 2.2, 2.21]; % S1固相浓度
liquid_s2 = [0.401, 0.327, 0.28, 0.246, 0.255, 0.269, 0.186, 0.324, 0.354, 0.349, 0.352, 0.344, 0.347]; % S2液相浓度
solid_s2 = [1.84, 2.58, 3.05, 3.39, 3.3, 3.16, 2.99, 2.61, 2.31, 2.36, 2.33, 2.41, 2.33]; % S2固相浓度
liquid_s3 = [0.225, 0.086, 0.08, 0.078, 0.068, 0.085, 0.093, 0.138, 0.149, 0.171, 0.169, 0.172, 0.173]; % S3液相浓度
solid_s3 = [3.6, 5.09, 5.05, 5.07, 5.17, 4.8, 4.3, 4.41, 4.36, 4.14, 4.16, 4.13, 4.12]; % S3固相浓度
liquid_s4 = [0.367, 0.284, 0.224, 0.195, 0.174, 0.185, 0.202, 0.199, 0.197, 0.196, 0.199, 0.198, 0.199]; % S4液相浓度
solid_s4 = [2.18, 3.01, 3.61, 3.9, 4.11, 4, 3.83, 3.86, 3.88, 3.89, 3.86, 3.87, 3.86]; % S4固相浓度
% 第三个表格数据
initial_concentration = [0.0681, 0.137, 0.2177, 0.3302, 0.4324, 0.5338, 0.5842, 0.6222, 0.7062, 0.7956]; % 初始浓度
liquid_s1_iso = [0.0461, 0.0722, 0.1235, 0.215, 0.2951, 0.3716, 0.3969, 0.4547, 0.4852, 0.5714]; % S1等温平衡液相浓度
solid_s1_iso = [0.1702, 0.6005, 0.8921, 1.102, 1.323, 1.572, 1.823, 2.1, 2.16, 2.192]; % S1等温平衡固相浓度
liquid_s2_iso = [0.0246, 0.0492, 0.0903, 0.1725, 0.2563, 0.3376, 0.3574, 0.3701, 0.4352, 0.5043]; % S2等温平衡液相浓度
solid_s2_iso = [0.1852, 0.8301, 1.224, 1.527, 1.711, 1.912, 2.218, 2.471, 2.66, 2.863]; % S2等温平衡固相浓度
liquid_s3_iso = [0.0424, 0.0654, 0.1091, 0.2068, 0.2614, 0.3304, 0.3852, 0.4065, 0.4467, 0.5999]; % S3等温平衡液相浓度
solid_s3_iso = [0.2071, 0.6683, 1.036, 1.184, 1.66, 1.984, 1.94, 2.107, 2.545, 2.937]; % S3等温平衡固相浓度
liquid_s4_iso = [0.0354, 0.0613, 0.0993, 0.1931, 0.2528, 0.2879, 0.3568, 0.4195, 0.5071, 0.5061]; % S4等温平衡液相浓度
solid_s4_iso = [0.2772, 0.7101, 1.134, 1.321, 1.546, 1.781, 2.124, 1.977, 2.461, 2.845]; % S4等温平衡固相浓度
% 拟合吸附速率常数k
concentration = [0.483; 0.479; 0.452; 0.418; 0.371; 0.342; 0.319; 0.311; 0.309];
microbe_concentration = [1.5e7; 1.7e7; 2.0e7; 2.5e7; 3.0e7; 3.3e7; 3.5e7; 3.7e7; 3.7e7];
days = [0; 1; 2; 3; 4; 5; 6; 7; 8];
% 初始浓度
initial_concentration = concentration(1);
% 计算有机物浓度比
运行图:
再免费来一个我最开始用于数值模拟的代码吧,注意,只是我最开始用的,不是我最后实际求解用的完整代码:
% 仅为最开始我模拟的一个简易代码,不是我最后实际求解用的
% 完整论文及实际求解代码请点击本文章最下方我的个人卡片
% 定义参数
u = 38.67; % 平均孔隙流速
v = 5.01; % 地下水渗流流速
k = 6.32; % 渗透系数
D = 0.38; % 弥散系数
rho = 1.67; % 含水层样品的密度
n = 0.375; % 孔隙度
dt = 0.5; % 时间步长
dx = 1.0; % 空间步长
dz = 1.0; % 空间步长
% 定义网格大小和时间步数
N = 100; % 河流-地下水系统网格的长度
M = 100; % 总时间步数
% 初始化浓度矩阵
C = zeros(N, N);
C(:, 1) = 0.5; % 初始时刻浓度为0.5 mg/L
% 迭代求解
for j = 2:M
for i = 2:N-1
% 计算对流、弥散项
convective_term = u * dt / dx * (C(i-1, j-1) - C(i, j-1));
if j == 2
advective_term = v * dt / dz * (C(i, j-1) - C(i, j-1));
else
advective_term = v * dt / dz * (C(i, j-1) - C(i, j-2));
end
if j == 2
dispersive_term = D * dt / (dx^2) * (C(i+1, j-1) - 2*C(i, j-1) + C(i-1, j-1)) + D * dt / (dz^2) * (C(i, j) - 2*C(i, j-1) + C(i, j-1));
else
dispersive_term = D * dt / (dx^2) * (C(i+1, j-1) - 2*C(i, j-1) + C(i-1, j-1)) + D * dt / (dz^2) * (C(i, j) - 2*C(i, j-1) + C(i, j-2));
end
% 更新浓度
C(i, j) = C(i, j-1) - convective_term - advective_term + dispersive_term;
end
% 更新边界条件
% C(边界处, j) = 根据边界条件确定的值
end
% 输出结果
%可视化结果
time = (0:M-1) * dt; % 时间轴,单位为小时
plot(time, C(:, 1)); % 绘制浓度随时间的变化曲线
xlabel('时间 (小时)');
ylabel('浓度 (mg/L)');
title('24小时内的浓度变化');
% 仅为最开始我模拟的一个简易代码,不是我最后实际求解用的
% 完整论文及实际求解代码请点击本文章最下方我的个人卡片
OK,就讲到这里吧,实在太累了,讲解得可能不够详细,详细的讲解视频、我实际求解用到的完整代码还有我的完整论文等请点击下方我的个人卡片查看哈↓: