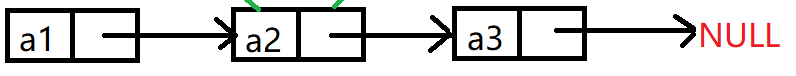【数据结构】(二)顺序表、链表结构的实现与对应操作详解
目录
- 1.线性表
-
- 1.1.1 概念
- 2.顺序表
-
- 2.1 概念及结构
-
- 2.1.1概念
- 2.1.2 结构
- 2.2 接口及实现
- 2.3顺序表的问题及思考
- 3.链表
-
- 3.1 链表的概念及结构
-
- 3.1.1 概念
- 3.1.2 结构
- 1.单链表、双向链表
- 2.不带头单链表、带头链表
- 3.单链表、循环单链表
- 3.2 链表的实现
-
- 3.2.1 无头单向非循环链表的实现
- 3.2.2 带头双向循环链表的实现
- 4.顺序表和链表的联系与区别
-
- 4.1 联系
- 4.2 区别
1.线性表
1.1.1 概念
线性表(linear list) 是n个具有相同特性的数据元素的有限序列。 线性表是一种在实际中广泛使用的数据结构,常见的线性表:顺序表、链表、栈、队列、字符串…
线性表在逻辑上是线性结构,也就说是连续的一条直线。但是在物理结构上并不一定是连续的,线性表在物理上存储时,通常以数组(物理上连续)和链式结构的形式存储。
2.顺序表
2.1 概念及结构
2.1.1概念
顺序表是用一段物理地址连续的存储单元依次存储数据元素的线性结构,一般情况下采用数组存储。在数组上完成数据的增删查改。
顺序表一般可以分为:
- 静态顺序表:使用定长数组存储。
- 动态顺序表:使用动态开辟的数组存储
#define SIZE 6
typedef int SLDataType;
//顺序表的静态存储
typedef struct SeqList
{
SLDataType array[SIZE];//定长数组
size_t size;//有效数据个数
}SeqList;
//顺序表的动态存储
typedef struct SeqList
{
SLDataType* array;//指向动态开辟的数组
size_t size;//有效数据个数
size_t capacity;//容量空间的大小
}
2.1.2 结构
静态存储的顺序表结构:

动态存储的顺序表结构:

静态顺序表只适用于确定知道需要存多少数据的场景。静态顺序表的定长数组导致N定大了,空间开多了浪费,开少了则不够用。因此现实中使用的基本都是动态顺序表,根据需要动态的分配空间大小,所以下面我们实现动态顺序表。
2.2 接口及实现
typedef int SLDataType;
typedef struct SeqList
{
SLDataType* array;
int size;
int capacity;
}
// 顺序表初始化
void SeqListInit(SeqList *ps, int InitCapacity);
// 顺序表尾插
void SeqListPushBack(SeqList *ps, DataType data);
//顺序表尾删
void SeqListPopBack(SeqList *ps);
//顺序表在pos插入data
void SeqListInsert(SeqList *ps, int pos, DataType data);
//顺序表删除pos位置的值
void SeqListErase(SeqList *ps, int pos);
//顺序表的销毁
void SeqListDestroy(SeqList *ps);
//顺序表判空
int SeqListEmpty(SeqList *ps);
//顺序表查找
int SeqListSearch(SeqList *ps, DataType data);
//顺序表增容
void SeqListInse(SeqList *ps, int InseCapacity);
//获取顺序表有效元素的个数
int SeqListSize(SeqList *ps);
//获取顺序表当前容量
int SeqListCapacity(SeqList *ps);
//顺序表打印
void SeqListprint(SeqList *ps);
顺序表操作实现:
void SeqListInit(SeqList *ps, int InitCapacity)
{
assert(ps);
ps->array = (DataType*)malloc(sizeof(DataType)*InitCapacity);
if (NULL == ps)
return;
ps->capacity = InitCapacity;
ps->size = 0;
}
void CheckCapacity(SeqList *ps)
{
assert(ps);
if (ps->size == ps->capacity)
SeqListInse(ps, ps->capacity*2);
}
void SeqListPushBack(SeqList *ps, DataType data)
{
assert(ps);
//检查是否需要扩容
CheckCapacity(ps);
ps->array[ps->size++] = data;
}
void SeqListPopBack(SeqList *ps)
{
assert(ps);
if (SeqListEmpty(ps))
return;
ps->size--;
}
void SeqListInsert(SeqList *ps, int pos, DataType data)
{
assert(ps);
if (pos > ps->size || pos<0)
{
printf("位置非法!!\n");
return;
}
CheckCapacity(ps);
for (int i = ps->size-1; i > pos; i--)
{
ps->array[i] = ps->array[i - 1];
}
ps->array[pos] = data;
ps->size++;
}
void SeqListErase(SeqList *ps, int pos)
{
assert(ps);
if (pos > ps->size-1 || pos < 0)
{
printf("位置非法!!\n");
return;
}
for (int i = pos; i < ps->size-1; i++)
{
ps->array[i] = ps->array[i + 1];
}
ps->size--;
}
void SeqListDestroy(SeqList *ps)
{
assert(ps);
free(ps->array);
ps->array = NULL;
ps->capacity = 0;
ps->size = 0;
}
int SeqListEmpty(SeqList *ps)
{
assert(ps);
if (0 == ps->size)
return 1;
return 0;
}
int SeqListSearch(SeqList *ps, DataType data)
{
assert(ps);
if (SeqListEmpty(ps))
{
printf("顺序表为空,无法查找!!\n");
return -1;
}
for (int i = 0; i < ps->size; i++)
{
if (data == ps->array[i])
return i;
}
printf("找不到!!\n");
return -1;
}
void SeqListInse(SeqList *ps, int InseCapacity)
{
assert(ps);
if (InseCapacity <= (ps)->capacity)
return;
ps->array = (DataType*)realloc(ps->array, sizeof(DataType)*InseCapacity);
assert(ps->array);
ps->capacity = InseCapacity;
}
int SeqListSize(SeqList *ps)
{
assert(ps);
return ps->size;
}
int SeqListCapacity(SeqList *ps)
{
assert(ps);
return ps->capacity;
}
void SeqListprint(SeqList *ps)
{
assert(ps);
for (int i = 0; i < ps->size; i++)
{
printf("%d ", ps->array[i]);
}
printf("\n");
}
2.3顺序表的问题及思考
- 中间/头部的插入删除,时间复杂度为O(N)
- 增容需要申请新空间,拷贝数据,释放旧空间。会有不小的消耗,对效率有影响。
- 增容一般是呈2倍的增长,势必会有一定的空间浪费。例如当前容量为100,满了以后增容到200,我们再继续插入了5个数据,后面没有数据插入了,那么就浪费了95个数据空间。
根据顺序表的特点,思考其应用场景,以及相比于链表的优势与不足。
3.链表
3.1 链表的概念及结构
3.1.1 概念
链表是一种物理存储结构上非连续,非顺序的存储结构,数据元素的逻辑顺序是通过链表中的指针链接次序实现的。即链表是逻辑连续的。
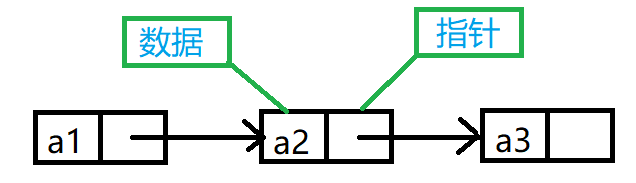
3.1.2 结构
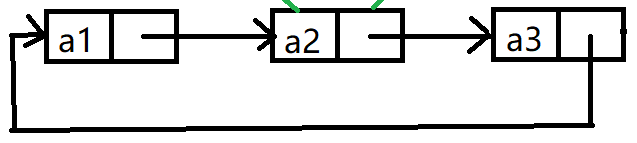
实际中链表的结构非常多,以下情况组合起来就有八种链表结构:
1.单向,双向
2.带头,不带头
3.循环,非循环
1.单链表、双向链表
2.不带头单链表、带头链表
3.单链表、循环单链表
1.无头单向非循环链表
结构简单,一般不会单独用来存数据,更多是作为卡数据结构的子结构,如哈希桶、图的邻接表等等。
2.带头双向循环链表

结构最复杂,一般用在单独存储数据。实际中使用的链表数据结构都是带头双向循环链表。这个结构虽然复杂,但是该结构在使用时会带来很多优势,操作反而更简单。
3.2 链表的实现
3.2.1 无头单向非循环链表的实现
typedef int DataType;
typedef struct SListNode
{
DataType val;
struct SListNode* next;
}Node;
//单链表初始化,理论上无头单向非循环链表不需要初始化
//需要修改头指针指向的函数均需要传二级指针
void SListInit(Node** phead);
//动态申请一个节点
Node* BuySListNode(DataType data);
//单链表尾插
void SListPushBack(Node** phead,DataType data);
//单链表尾删
void SListPopBack(Node** phead);
//单链表头插
void SListPushFront(Node** phead, DataType data);
//单链表头删
void SListPopFront(Node** phead);
//单链表任意位置插入
void SListInsert(Node* pos, DataType data);
//单链表任意位置删除
void SListErase(Node* pos);
//单链表查找
Node* SListFind(Node* head);
//求链表中节点个数
int SListSize(Node* head);
//单链表打印
void SListPrint(Node* head);
代码实现:
#include 3.2.2 带头双向循环链表的实现
//带头结点的双向循环链表
typedef int DataType;
typedef struct DListNode
{
struct DListNode* prev;//指向前一个节点
struct DListNode* next;//指向后一个节点
DataType val;
}Node;
//思考什么时候该传二级指针??
// 创建返回链表的头结点.
void DListInit(Node** phead);
//创建双向链表新节点
Node* BuyDListNode(DataType data);
//双向链表尾插
void DListPushBack(Node* head, DataType data);
//双向链表尾删
void DListPopBack(Node* head);
//双向链表头插
void DListPushFront(Node* head, DataType data);
//双向链表头删
void DListPopFront(Node* head);
//双向链表查找
Node* DListFind(Node* head, DataType data);
//双向链表在pos的前面进行插入
void DListInsert(Node* pos, DataType data);
//双向链表删除pos位置的节点
void DListErase(Node* pos);
// 双向链表销毁
void DListDestroy(Node** phead);
// 双向链表打印
void PrintDList(Node* head);
代码实现:
#include "DList.h"
#include 带头节点链表的插入和删除将会更加方便,无头单链表在插入时如果为空链表元素而需要考虑修改头指针,在删除时如果只有一个元素也要修改头指针,造成了不便,加入了存放无效值的头节点则轻松解决了这个问题。
4.顺序表和链表的联系与区别
4.1 联系
顺序表和链表都是逻辑上连续的数据结构,它们将一组类似数据有效的组织起来。
4.2 区别
| 顺序表 | 链表 | |
|---|---|---|
| 存储空间 | 连续空间 | 不一定连续 |
| 插入/删除时间复杂度 | 搬移元素O(N) | 不需要搬移元素O(1) |
| 随机访问 | 支持O(1) | 不支持O(N) |
| 获取下一元素方式 | 下标++/- - | next/prev |
| 插入 | 可能需要扩容 | 没有容量一说,需要时就申请空间 |
| 空间 | 扩容时才需要申请空间 | 如果插入的元素比较多,需要频繁向堆申请小的内存块,产生内存碎片(缺陷) |
| 应用场景 | 元素高效存储/频繁访问 | 任意位置频繁插入/删除 |
| 缓存利用率 | 高 | 低 |