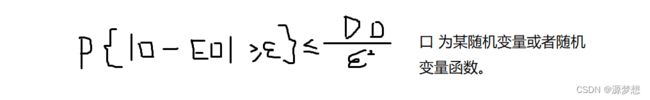切比雪夫不等式，大数定律及极限定理。

一.切比雪夫不等式

1.定理

若随机变量X的期望EX和方差DX存在,则对任意ε > 0,有
  P{ |X - EX| >= ε } <= DX/ε² 或 P{ |X - EX| < ε } >= 1 - DX/ε²

2.解析定理

①该定理对 X 服从什么分布不做要求，仅EX DX存在即可。

②“| |” 由于X某次试验结果可能大于期望值，也可能小于期望值，但总在其旁边波动，所
以加"| |"。

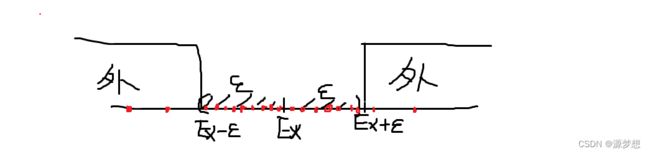
③根据期望定义知，N次试验X的取值，总是徘徊在EX的附近，即 (EX - ε, EX + ε) 之间的可能性很大很大, 而落在 外边 的概率应特别小，比 DX/ε² 还要小。

3.关于 DX/ε²

①DX为方差，DX越小，波动性越小，则N次X取值分布就越集中，则落在外边的概率就越小，则P{ |X - EX| >= ε } 就越小。

②DX为方差，影响不等式的因素之一，但切比雪夫不等式也反过来证明了DX存在的意义：
  由不等式知DX越小，P{ |X - EX| >= ε }越小，X分布越集中于EX。这表明方差DX是 刻画随机变量与其期望值偏离程度的量 ，是描述随机变量X “分散程度” 特征的指标。故DX也属于X的数字特征之一。

4.证明切比雪夫不等式

5.广义化切比雪夫不等式

6.切比雪夫不等式应用

①可以估算随机变量X在某范围取值的概率

②可以证明某些收敛性问题(如：证明大数定理)
后面有

二.依概率收敛

1.通常认知的收敛与依概率收敛的区别

①我们通常认知的收敛：（以数列收敛为例）
  an -> a : ∀ε > 0 , ョN > 0, 当 n > N 时 ，总有 “|Xn - a| < ε”.
即存在某一项，这项后面的所有项都绝对落在区域(a - ε , a + ε)之间。

②依概率收敛：
  Xn - X：∀ε > 0 , ョN > 0, 当 n > N 时 ,“有概率为1的可能” 使 “|Xn - a| < ε”.
即存在某一项，这项后面所有项，“有概率为1的可能” 落在区间为(X - ε, X + ε)之间。

注：我们知道概率为 1 的事件 未必是绝对事件，所以 在某项之后的所有项中 ，还是有极少不听话的 “X” 落在了(X - ε, X + ε) 之外，但不影响整体的敛散性。

综上就是 “依概率收敛” 和 “收敛” 的区别：
  ①收敛：在某项之后，是绝对趋于某值的,有且仅有一直逼向某值的可能。
  ②依概率收敛：在某项之后，未必绝对趋于某值，因为概率为1得事件未必是绝对事件。
(概率为1 < 绝对)
这就是为啥叫依概率收敛。（依的就是这个1，X在某项之后的所有项，有1的概率会落在(X - ε, X + ε)之间）

2.举个例子理解依概率收敛,以及为啥会出现依概率收敛。

例子：若我们抛出了N次硬币，N 很大很大很大。N是偶数。出现正面的次数为 N/2，N/2次反面。

①按照通常收敛定义知: 如果我们再次抛出硬币 k 次。那么，这k次后，Xn的概率应该只能更加逼近 1/2.而不可能出现其他情况。
但事实上，我们很有可能在再抛出k次之后 Xn的概率会变成 1/3。故通常的收敛已经不适用如上场景。

②依概率收敛: 当抛出 N 次后 Xn概率为 1/2后。再抛出k 次统计正面朝上概率为1/2的概率是1。但是概率为1的事件未必是绝对事件，只是可能性很大很大很大，但还是有可能出现其他概率的不为1/2了。这就完美了描述了上述场景。

三.大数定律

1.伯努利大数定律

注：伯努利大数定律告诉我们，当试验次数足够大时，用频率估算概率这件事是可靠的。

①伯努利大数定理

n趋向于无穷大时，事件A在n重伯努利事件中发生的频率fn/n无限接近于事件A在一次实验中发生的概率p。

②证明伯努利大数定理（夹逼准则+切比雪夫不等式）

2.切比雪夫大数定律

①切比雪夫大数定律

注1：X1,X2…Xn两两不相关。
注2：X1,X2…Xn不要求同分布。
注3：仅要求EXi DXi存在且DXi有界。
注4：这个表达式是由伯努利大数定理推出来的。基于“频率 估算 概率“的可靠性来的。

②证明切比雪夫大数定律

3.切比雪夫大数定律推论

注1：不相关 弱化为 独立
注2：无分布要求 弱化为 同分布
注3：Exi Dxi存在 弱化为 有具体值。
一般就考这个，因为更一般化的不好出题。

4.辛钦大数定律

将切比雪夫大数定律推论的条件再次弱化。即去掉方差要求，即为辛钦大数定律。

此结论依然成立。
注：重点常用这个，因为条件弱化更容易出题。

5.总结大数定律

①伯努利大数定律给出：
  用频率估算概率这件事是靠谱的。
(即当试验总够大，频率 依概率收敛 于它的概率)
(用夹逼+切比雪夫不等式证明)

②基于“频率 依概率收敛于 概率”的可靠性，得出“切比雪夫大数定律”及其推论。
(即当Xi互不相关，EXi DXi 存在且DXi有界，∀ε >0有X均值 依概率收敛 于数学期望的均值)
(推论：即Xi相互独立，Exi = u,DXi = σ²，∀ε >0有X均值 依概率收敛 于数学期望u)
(用夹逼+切比雪夫不等式证)

③基于"切比雪夫大数定律推论"弱化其条件，得到辛钦大数定律。
(即Xi相互独立，Exi = u，∀ε >0有X均值 依概率收敛 于数学期望u)

④大数定律告诉我们两件事：
用频率估算概率很靠谱。
用X的均值估算X数学期望很靠谱。

四.中心极限定理

先略。