时间序列预测的20个基本概念总结
1、时间序列
时间序列是一组按时间顺序排列的数据点
比如:
- 每小时的气压
- 每年的医院急诊
- 按分钟计算的股票价格
2、时间序列的组成部分
时间序列数据有三个主要组成部分。
- 趋势
- 季节性
- 残差或白噪声
3、趋势
在时间序列中记录的长期缓慢变化/方向。
4、季节性
季节性是在固定时间内发生的时间序列中的循环模式。
下面的时间序列显示了季节性,在每个周期中,都处于底部和峰值,模式相似。
5、残差/白噪声
这是一个时间序列的模式,完全是随机的,不能用趋势或季节成分来解释。
6、时间序列分解
时间序列分解是将时间序列分解为其组成部分的过程,即趋势,季节性和残差。
在上图显示了时间序列数据,数据下面的图中被分解为其组成部分。
“残差”显示的是时间序列中无法用趋势或季节性解释的模式。这些表示数据中的随机性。
我们可以使用如下所示的statmodels库来分解时间序列。
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.seasonal import STL
df = pd.read_csv("time-series-data.csv")
decomposition = STL(df['x'], period=12).fit()
decomposition可以进一步绘制如下:
fig, (ax1, ax2, ax3, ax4) = plt.subplots(nrows=4, ncols=1, sharex=True,figsize=(10,8))
ax1.plot(decomposition.observed)
ax1.set_ylabel('Observed')
ax2.plot(decomposition.trend)
ax2.set_ylabel('Trend')
ax3.plot(decomposition.seasonal)
ax3.set_ylabel('Seasonal')
ax4.plot(decomposition.resid)
ax4.set_ylabel('Residuals')
plt.tight_layout()
7、时间序列预测
预测是基于历史时间数据在以后时间上进一步预测数据点的过程。
这可以使用统计模型来完成,例如:
- 自回归(AR)模型
- 移动平均(MA)模型
- 自回归移动平均(ARMA)模型
- 自回归综合移动平均(ARIMA)模型
- 季节自回归综合移动平均(SARIMA)模型
- 带有外源回归量的季节自回归综合移动平均(SARIMAX)模型
- 向量自回归(VAR)模型
- 矢量误差校正(VECM)模型
对于较大的数据集,使用以下提到的深度学习模型:
- 多层感知器(MLP)
- 循环神经网络(RNN)
- 长短期记忆网络(LSTM)
- 自回归LSTMs
- 卷积神经网络(CNN)
8、预测范围
根据历史时间序列数据预测未来数据点的时间段。
例如根据10年记录的每日气温数据,预测下一周的气温。
在这种情况下,预测范围是一周的时间。
9、预测模型基本步骤
时间序列预测模型主要由以下步骤组成:
- 收集时间序列数据
- 开发预测模型
- 将模型部署到生产环境中
- 收集新数据
- 监控和评估模型性能
- 重新训练预测模型
- 将新模型部署到生产环境中
- 返回步骤4
10、时间序列预测与回归
下面是时间序列预测与回归任务的主要区别。
时间序列数据是有序的。这意味着观察/数据点依赖于以前的观察/数据点。因此,在模型训练期间,数据点顺序不会被打乱。
时间序列预测处理随时间收集的数据。而回归可以处理不同类型的数据。
11、Naïve预测与基线模型
基线模型是使用naïve对时间序列数据进行预测构建的最简单的模型。作为比较其他预测模型的基线。
以下假设可用于创建基线模型:
- 未来值与时间序列中的最后一个数据点相同
- 未来值与某一时期内的值的中位数/众数相同
- 未来的值等于一定时期内的平均值
- 未来的值与一定时期内的所有值相同
12、错误指标
准确预测的目的是最小化数据中预测值与实际值之间的差距。所以有各种错误指标用于监视和最小化这种差距。
常用的误差指标如下:
- 均方误差 (MSE)
- 平均绝对误差 (MAE)
- 均方根误差 (RMSE)
- 平均绝对百分比误差 (MAPE)
13、平稳性
平稳的时间序列是其统计性质不随时间变化的序列,这些统计属性包括:
- 均值
- 方差
- 自相关性
一般的统计预测方法(AR、MA、ARMA)都假定时间序列是平稳的。所以如果非平稳时间序列数据与这些一起使用,结果将是不可靠的。
14、变换
变换可以认为是使时间序列平稳的数学过程。常用的变换有:
差分计算从一个时间步到另一个时间步的变化。有助于在时间序列数据中获得恒定的均值。
要应用差分,我们只需从当前时间步长的值中减去之前时间步长的值。
一阶差分:对数据应用一次的差分;二阶差分:对数据应用两次的差分
对数函数应用于时间序列以稳定其方差,但是对数变换后需要进行逆向变换,将最终的结果进行还原。
15、Dickey-Fuller (ADF) 检验
Augmented Dickey-Fuller (ADF) Test是一种用于时间序列数据的经济统计学检验方法,用于确定一个时间序列是否具有单位根(unit root)。单位根表示时间序列具有非平稳性,即序列的均值和方差不随时间变化而稳定。ADF测试的目的是确定时间序列是否具有趋势,并且是否可以进行经济统计学分析。
ADF测试的核心假设是,如果时间序列具有单位根,则序列是非平稳的。反之,如果序列不具有单位根,则序列是平稳的。ADF测试通过对序列进行回归分析来验证这些假设。
我们可以直接使用statsmodels来进行这个检验
from statsmodels.tsa.stattools import adfuller
ADF_result = adfuller(time_series)
print(f"ADF Result Value: {ADF_result[0]}")
print(f"ADF Result p-value: {ADF_result[1]}")
16、自相关
是对时间序列中由不同时间步长隔开的值之间线性关系的度量。滞后是分隔两个值的时间步数。
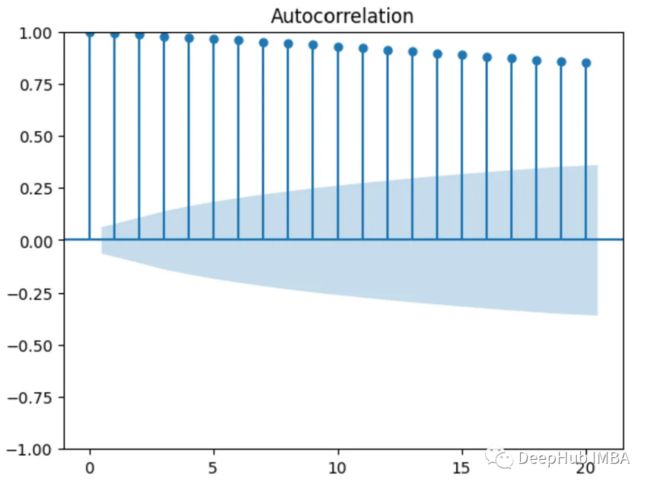
自相关函数(ACF)图用于测试时间序列中的值是否随机分布或彼此相关(如果时间序列具有趋势)。
from statsmodels.graphics.tsaplots import plot_acf
plot_acf(time_series, lags = 20)
这里的x轴上的值表示滞后,y轴上的值表示由滞后分隔的不同值之间的相关性。
如果y轴上的任何值位于图的蓝色阴影区域,则该值在统计上不显著,比如下面的ACF图显示其值之间没有相关性(除了第一个与自身相关的值)。
17、平滑方法
平滑方法(Smoothing Methods)是一种用于对时间序列数据进行平滑处理的技术,以便更好地观察数据的趋势和季节性成分。这些方法的目标是减少随机噪声,突出数据中的长期变化模式。
常见的有:移动平均法(Moving Average Method)、加权移动平均法(Weighted Moving Average Method)、指数平滑法(Exponential Smoothing Method)、季节性平滑法(Seasonal Smoothing Method)
18、时间序列数据特征
- 静态时间序列(Static Time Series):静态时间序列是指数据在时间上没有变化的情况下进行分析。也就是说,它假设观测到的时间序列数据是固定的,没有随时间的推移而发生变化。在静态时间序列中,我们通常关注数据的平均水平、趋势和季节性等静态特征。常见的静态时间序列模型包括平均数模型、指数平滑模型和ARIMA模型等。
- 动态时间序列(Dynamic Time Series):动态时间序列是指数据在时间上呈现出变化的情况下进行分析。也就是说,它认为观测到的时间序列数据是随时间变化的,并且过去的值对未来的值有影响。在动态时间序列中,我们关注数据的动态性、趋势变化和周期性等动态特征。常见的动态时间序列模型包括自回归移动平均模型(ARMA)、自回归积分滑动平均模型(ARIMA)和向量自回归模型(VAR)等。
静态时间序列假设数据在时间上没有变化,主要关注数据的静态特征。动态时间序列考虑数据在时间上的变化,并关注数据的动态特征。静态时间序列可以看作是动态时间序列的特例,当数据在时间上没有变化时,可以将其视为静态时间序列。
19、季节性(Seasonality),循环性(Cyclicity) 区别
季节性(Seasonality)和循环性(Cyclicity)都是描述时间序列数据中重复出现的模式,但它们之间存在一些区别。
季节性是在较短的时间尺度内,由于固定或变化的季节因素引起的周期性模式,而循环性则是在较长时间尺度内,由于经济或其他结构性因素引起的周期性模式。
季节性(Seasonality)是指时间序列数据中由于季节因素引起的重复模式。这种模式通常是在较短的时间尺度内(例如每年、每季度、每月或每周)出现的,并且在不同时间段内的观测值之间存在明显的相似性。季节性可以是固定的,即在每个季节周期内的模式相对稳定,例如每年夏天都有高温;也可以是非固定的,即在季节周期内的模式可能有变化,例如某个季节的销售量在不同年份间波动。
循环性(Cyclicity)是指时间序列数据中具有较长周期性的模式。这种模式的周期可以大于或小于季节周期,并且循环性的持续时间通常比季节性更长。循环性可能是由经济、商业或其他结构性因素引起的,与季节性不同,循环性的模式不一定按照固定的时间间隔出现,而是根据外部因素的影响而变化。例如,房地产市场的周期性波动就是一个循环性的例子。
20、时间序列库推荐
PyFlux: PyFlux是一个用于时间序列分析和建模的库,提供了多种模型,包括ARIMA、GARCH、VAR等。
PyCaret: PyCaret是一个用于机器学习和自动化建模的库,它提供了简化时间序列预测任务的工具。它支持自动特征选择、模型选择和调优等功能,可以快速构建时间序列预测模型。
sktime: sktime是一个专门用于时间序列数据的机器学习库,它建立在scikit-learn之上,并提供了许多专门针对时间序列的预处理和建模技术。
CausalImpact: CausalImpact是一个用于因果效应分析的库,它可以帮助评估时间序列数据中某个事件或处理对结果的影响。
tsfresh: tsfresh是一个用于提取时间序列特征的库,它提供了各种统计和时间特征提取方法,用于时间序列数据的特征工程。
https://avoid.overfit.cn/post/7bc21f124d284b47becbeca6dc5c07c7
作者:Ashish Bamania