ADC前级滤波的解释

本为引用了微芯应用笔记 ：AN699文档 地址为https://ww1.microchip.com/downloads/en/Appnotes/00699b.pdf

介绍模拟滤波器几乎可以在每一个电子电路中找到。音频系统使用它们进行预放大、均衡和音调控制。在通信系统中，滤波器用于调谐特定的频率并消除其他频率。数字信号处理系统使用滤波器来防止带外噪声和干扰的混叠。本应用笔记研究减少数据采集系统中外来噪声影响的模拟滤波器的设计。这些类型的系统主要使用低通滤波器、数字滤波器或两者的结合。使用模拟低通滤波器，可以在模数转换(A/D)之前从信号路径中去除高频噪声和干扰。通过这种方式，转换的数字输出码不包含不需要的杂化谐波信息。相比之下，数字滤波器可以利用平均技术来降低带内频率噪声。虽然应用笔记是关于模拟滤波器的，但第一部分将比较模拟滤波策略与数字滤波的优点。在此比较之后，定义了模拟滤波器的设计参数。在讨论低通滤波器的频率特性时，也将参考一些特定滤波器的设计。在第三部分，将深入讨论低通滤波器的设计。本应用笔记的下一部分将讨论如何确定抗混叠滤波器的适当滤波器设计参数的技术。本节将讨论混叠理论。然后是运算放大器滤波电路。我们也将讨论有源和无源低通滤波器的例子。最后给出了一个12位电路的设计实例。本应用笔记中讨论的所有有源模拟滤波器都可以使用Microchip的FilterLab软件进行设计。FilterLab将计算电容和电阻值，以及确定应用程序所需的极点数。该程序还将生成一个SPICE宏模型，可用于香料模拟。

模拟与数字滤波器包括模拟滤波器、数字滤波器或两者的系统如图1所示。当一个模拟滤波器实现时，它是在模数转换之前完成的。相反，当数字滤波器被实现时，它是在模数转换之后完成的。在这些特定的点上实现两个过滤器的原因是显而易见的，但是，这些限制的后果并不那么明显。

模拟信号输入——>模拟低通滤波——>AD转换——>数字滤波
图1:数据采集系统信号链可以利用模拟或数字滤波技术或两者的结合。当在数字域而不是模拟域提供滤波功能时，会有一些系统差异，用户应该意识到这些差异。模拟滤波可以在模拟信号到达模数转换器之前去除叠加在模拟信号上的噪声。特别是，这包括无关的噪声峰值。数字滤波不能消除模拟信号上的这些峰值。因此，信号上的噪声峰值有可能使A/D转换器的模拟调制器饱和。这是真的，即使信号的平均值“在限制之内”。此外，模拟滤波更适用于高速系统，即大约5kHz以上。在这些类型的系统中，模拟滤波器可以降低带外频率区域的噪声。这反过来又减少了折叠信号(请参阅本应用笔记中的“抗混叠滤波器理论”部分)。获得高分辨率的任务落在A/D转换器上。相比之下，数字滤波器的定义是使用过采样和平均技术来降低带内和带外噪声。这两个过程需要时间。由于数字滤波发生在A/D转换过程之后，它可以去除转换过程中注入的噪声。模拟滤波不能做到这一点。此外，数字滤波器可编程性更强比模拟滤波器容易。根据数字滤波器的设计，用户可以编程截止频率和输出数据率。

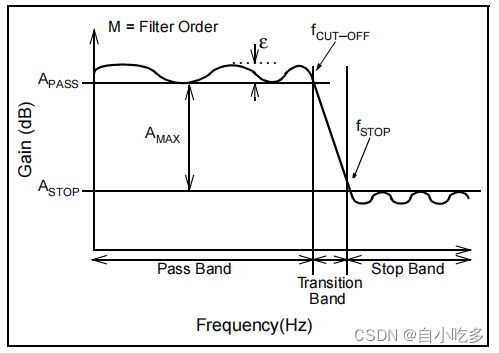
低通模拟滤波器设计的关键参数一个低通模拟滤波器可以用如图2所示的四个参数((fCUT-OFF, fSTOP,AMAX, and M)来指定。低通滤波器的截止频率(fCUT-OFF)定义为巴特沃斯和贝塞尔滤波器的-3dB点，或滤波器响应离开切比雪夫的误差带的频率。

从直流到截止频率的频率跨度被定义为通带区域。通过带中的响应大小定义为apass，如图2所示。通带内的响应可以是平坦的，没有纹波滤波器或贝塞尔滤波器。相反，切比雪夫滤波器的纹波上升到截止频率。一个滤波器的纹波误差的大小被定义为ε。

根据定义，一个低通滤波器通过较低的频率到截止频率，并衰减高于截止频率的较高的频率。一个重要的参数是滤波器系统的增益，AMAX。这被定义为在通带区域的增益与在停止带区域或 AMAX = APASS − ASTOP中获得的增益之间的差值。

在滤波器在通带中有纹波的情况下，通带(apass)的增益被定义为纹波的底部。停止频带频率fSTOP是达到最小衰减的频率。虽然停止带可能有纹波，但该纹波的最小增益(ASTOP)定义在最高峰值。

当滤波器的响应超过截止频率时，它通过过渡带下降到停止带区域。过渡带的带宽由滤波器设计（巴特沃斯、贝塞尔、切比雪夫等）决定。以及过滤器的顺序(M)。滤波器的顺序由传递函数中的极点数决定。例如，如果一个滤波器在其传递函数中有三个极点，它可以被描述为一个三阶滤波器。

一般来说，当使用更多的极点来实现滤波器设计时，过渡带宽会更小。图3中的巴特沃斯滤波器说明了这一点。理想情况下，一个低通、抗锯齿的滤波器应该采用“砖墙”风格的响应，其中过渡带被设计得尽可能小。实际上，这可能不是抗锯齿解决方案的最佳方法。采用主动滤波器设计，每两个极点都需要一个运算放大器。例如，如果设计了一个32阶滤波器，则需要16个操作放大器、32个电容和多达64个电阻来实现该电路。此外，每个放大器将贡献偏移和噪声误差到响应的通带区域。

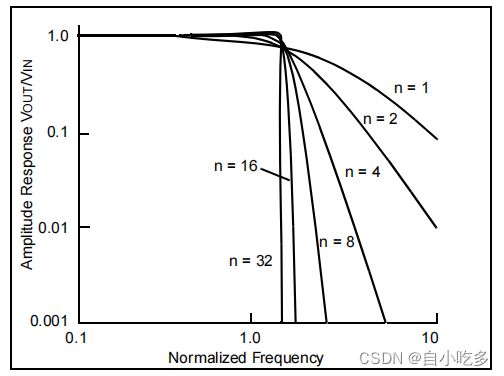
图3：在低通滤波器实现中使用了巴特沃斯设计，以获得频率依赖于滤波器的极点数或阶数(M)的各种响应。

模拟滤波器设计
更受欢迎的滤波器设计是巴特沃斯、贝塞尔和切比雪夫。每个滤波器的设计都可以通过图2中所示的四个参数来识别。本应用说明中未讨论的其他滤波器类型包括逆切比雪夫型、椭圆型和Cauer设计。

巴待沃思滤波器
巴特沃斯滤波器是目前为止在电路中最流行的设计。一个巴特沃斯滤波器的传递函数由所有极点和无零组成，并等同于：
VOUT /VIN = G/(a0sn + a1sn-1 + a2sn-2… an-1s2 + ans + 1)
其中G等于系统的增益。

表1列出了巴特沃斯设计的分母系数。虽然巴特沃斯滤波器设计的阶数理论上可以是无限的，但这个表只列出了一个五阶滤波器的系数。

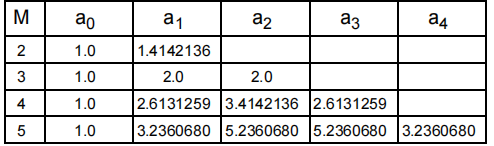
表1：巴特沃斯设计的系数与滤波器的顺序。

如图4a.所示，频率行为在通带中具有最大的平坦幅度响应。过渡带的衰减率优于贝塞尔，但不如切比雪夫滤波器。停止带中没有铃声。巴特沃斯曲线的阶跃响应如图5a所示。这种滤波器类型在时域上有一些超调和振铃，但比切比雪夫要少

契比雪夫滤波器
切比雪夫滤波器的传递函数仅与巴特沃斯滤波器相似，因为它具有所有极点和无零，其传递函数为：
VOUT/VIN = G/(a0 + a1s + a2s2+… an-1sn-1 + sn)

它的频率行为有一个纹波（图4b.）。在电路设计中由极的特定位置决定的通带。波纹的大小在图2中定义为ε。一般来说，纹波幅度的增加会减小过渡带的宽度。

表2给出了0.5dB纹波切比雪夫设计的分母系数。虽然切比雪夫滤波器设计的阶数理论上可以是无限的，但这个表只列出了一个五阶滤波器的系数。

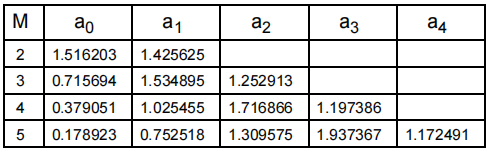
表2：1/2dB纹波切比雪夫设计的系数与滤波器的顺序。

过渡带的衰减率比巴特沃斯和贝塞尔滤波器更陡。例如，如果要满足一个三阶切比雪夫的跃迁带宽，则需要一个五阶巴特沃斯响应。虽然用这个滤波器在通带区域有振铃，但停止带没有振铃。步跃响应（图5b.）有相当程度的超调和铃声。

贝塞尔滤波器
同样，贝塞尔滤波器的传递函数只有极点，没有零。当巴特沃斯设计为最大平通带响应进行优化时，切比雪夫可以很容易地调整以最小化过渡带宽时，贝塞尔滤波器在大频率范围内对频率产生恒定的时间延迟。在数学上，这种关系可以表示为：
C = −∆θ * ∆f

C是常数，θ为相位，单位为度，f为频率，单位为Hz，
或者，该关系可以用每弧度表示为：
C = −∆θ / ∆ω
ω是用雷达表示的。

贝塞尔滤波器的传递函数为：
VOUT/VIN = G/(a0 + a1s + a2s2+… an-1sn-1 + sn)
贝塞尔滤波器的分母系数如表3所示。虽然贝塞尔滤波器设计的阶数理论上可以是无限的，但这个表只列出了一个五阶滤波器的系数。

表3：贝塞尔设计的系数与滤波器的顺序。

贝塞尔滤波器在通带上具有平坦的幅度响应(图4c)。在通带之后，过渡带的衰减速率比巴特沃斯或切比雪夫要慢。最后，在停止带中没有铃声。这个滤波器具有上述所有滤波器的最佳步长响应，很少有超调或振铃(图5c.)。

a)第五阶巴特沃斯滤波器 第5阶切比雪夫，带有0.5dB的波纹波 c)第五阶贝塞尔滤波器

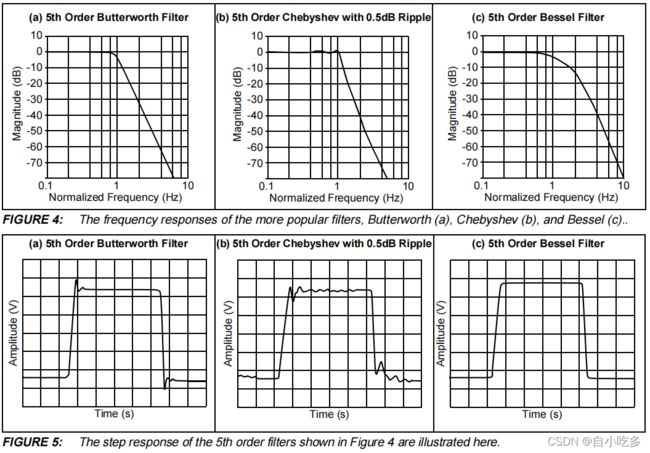
图4：更流行的滤波器的频率响应，巴特沃斯(a)，切比雪夫(b)，和贝塞尔©.。
图5：图4中所示的第5阶滤波器的阶跃响应如图4所示

反混叠滤波器理论
当将模拟信号数字化时，A/D转换器通常以恒定的采样频率工作。通过使用一个采样频率(fS)，通常称为奈奎斯特率，所有频率低于fS/2的输入信号都被可靠地数字化。如果输入信号的一部分位于fS/2以上的频域内，该部分将折叠回感兴趣的带宽。这种现象使得无法辨别来自较低频率（fS/2以下）和较高频率（fS/2以上）的信号之间的差异。

这种混叠或后折叠现象如图6中的频域所示。

图6：在fs(a)处对输入信号进行采样的系统将识别频率低于fs/2和以上的信号。fs/2以下的输入信号将被可靠地数字化，而fs/2以上的信号将被折叠回(b)，并在数字输出中以较低的频率出现。

在此图的两个部分中，x轴表示采样系统的频率，fS。在图6的左侧部分，确定了频带的五个频段。段N=0的跨度从DC到采样率的一半。在此带宽中，采样系统将可靠地记录模拟输入信号的频率内容。在其中N>0的段中，数字化系统将以段N=0的带宽记录模拟信号的频率内容。从数学上讲，这些更高的频率将用以下方程式折叠起来：

例如，让该系统的采样率(fS)等于100kHz，且其频率内容为：
fIN(1) = 41kHz
fIN(2) = 82kHz
fIN(3) = 219kHz
fIN(4) = 294kHz
fIN(5) = 347kHz

采样的输出将包含所有这些输入信号的准确振幅信息，但是，其中四个将被折叠回DC到fS/2或DC到50kHz的频率范围。利用fOUT=|fIN-NfS|公式，将输入信号的频率转换为：

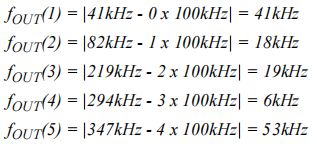
注意，所有这些信号频率都在DC和fS/2之间，振幅信息被可靠地保留

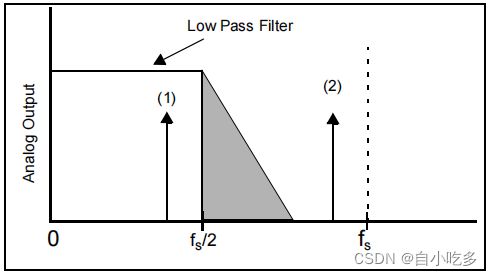
这种频率折叠现象可以通过使用A/D转换器输入之前的模拟低通滤波器来消除或显著减少。这个概念如图7所示。在该图中，低通滤波器在频率（2）处衰减输入信号的第二部分。因此，该信号将不会被混叠到最终的采样输出中。图7中所示的模拟低通滤波器有两个区域。左侧的区域在直流到fS/2的带宽范围内。第二个区域，即阴影部分，说明了滤波器的过渡带。由于该区域大于fS/2，因此该频带内的信号将被混叠到采样系统的输出中。通过移动滤波器的转角频率低于fS/2或增加滤波器的顺序，可以最小化该误差的影响。在这两种情况下，在fS/2时，滤波器的最小增益ASTOP应小于采样系统的信噪比(SNR)。

例如，如果使用12位a/D转换器，理想的信噪比是74dB。滤波器的设计应使其在fSTOP处的增益至少比通带增益小74dB。假设在本例中使用了一个五阶滤波器：

图7：如果采样系统在采样机制之前有一个低通模拟滤波器，则高频信号将被衰减而不被采样。

模拟滤波器实现
传统上，低通滤波器是用无源设备来实现的。电阻器和电容器。当需要高通或带通滤波器时，就会添加电感器。在当时，主动滤波器的设计是可实现的，然而，操作放大器的成本是令人望而却步的。当需要单极滤波器或滤波器的带宽比前沿操作放大器工作的频率更高时，无源滤波器仍然用于滤波器设计。即使有这两个例外，滤波器的实现主要是通过操作放大器，电容器和电阻来实现的

被动过滤器
采用电阻和电容器实现无源低通滤波器。单极和双极低通滤波器的实现如图8所示。

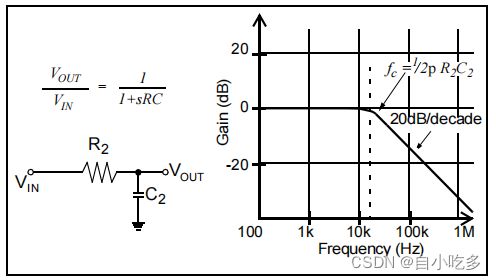
图8：电阻器和电容可用于实现无源、低通模拟滤波器。这种类型的滤波器实现的输入和输出阻抗等于r2。

与有源滤波器实现相比，无源低通滤波器的输出阻抗相对较高。例如，一个在设计中使用0.1µF电容器的1kHz低通滤波器将需要一个1.59kΩ的电阻来完成实现。这个电阻值可能会产生不希望的电压降或使阻抗匹配困难。因此，无源滤波器通常用于实现单个极点。单极运算放大器滤波器的额外好处是“隔离”滤波器的高阻抗从以下电路。

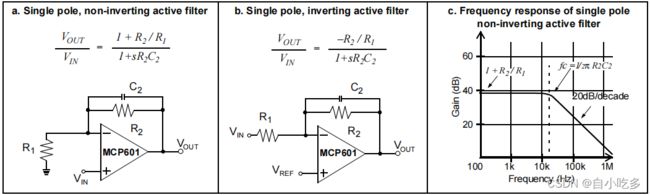
一个运算放大器结合两个电阻和一个电容，可用于实现一个一阶滤波器。这些有源滤波器的频率响应相当于一个单极无源低通滤波器。
在Delta-Sigma A/D转换器的输入端使用单极、低通、无源滤波器是非常常见的。在这种情况下，滤波器的高输出阻抗不干扰转换过程。

有源滤波器
有源滤波器使用一个放大器、一个到三个电阻和一到两个电容器的组合来实现一个或两个极。主动过滤器提供了在各个阶段之间提供“隔离”的优势。这是可以通过利用运算放大器的高输入阻抗和低输出阻抗来实现的。在所有情况下，滤波器的顺序都是由输入端和放大器的反馈回路中的电容器数量决定的。

单极滤波器
单极有源滤波器的频率响应与单极无源滤波器相同。单极有源滤波器实现的例子如图9所示。

双极点，受电压控制的电压源
双极电压控制电压源最好称为锁键滤波器实现。此滤波器被配置为使直流增益为正。在图10所示的下降键滤波器实现中，直流增益大于1。在图11所示的实现中，直流增益等于1。在这两种情况下，过滤器的顺序都等于2。这些滤波器的极点由r1、r2、C1和C2的电阻值和电容值决定

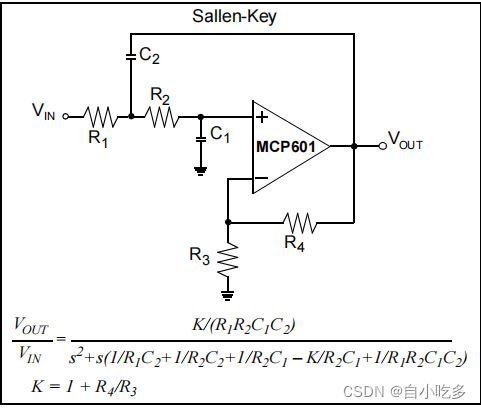
图10：双极或下降键滤波器实现有一个增益G=1+R4/R3。如果R3打开且R4短路，则直流增益等于1V/V。

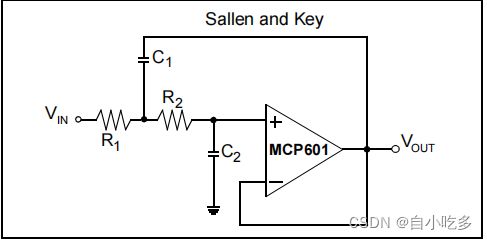
图11：具有直流增益的双极点或Sallen密钥滤波器实现等于1V/V。

双极多重反馈
一个二阶低通滤波器的双极、多重反馈实现如图12所示。这个过滤器也可以被简单地识别为一个多重反馈过滤器。该滤波器的直流增益使信号反转，等于r1和r2的比值。极点由r1、r3、c1和c2的值决定。

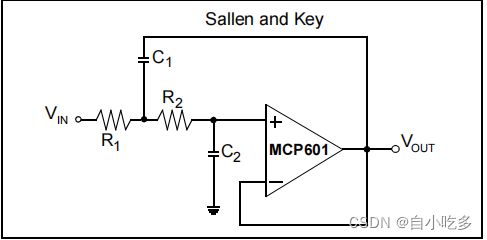
图12：一个双极，多反馈电路实现使用三个电阻和两个电容器来实现一个二阶模拟滤波器。直流增益等于-R2/R1。

抗混叠滤波器的设计示例
在以下示例中，图1中所示的数据采集系统信号链将被修改如下。模拟信号将直接进入一个有源低通滤波器。在本例中，模拟信号的带宽为直C到1kHz。低通滤波器的设计将使来自模拟输入的高频信号不通过A/D转换器，以试图消除混叠误差。该过滤器的实现和顺序将根据设计参数进行修改。排除滤波函数后，抗混叠滤波器不会进一步修改信号，即实现增益或反转信号。低通滤波器段之后将会有一个12位的SARA/D转换器。A/D转换器的采样率将为20kHz，使奈奎斯特的1/2等于10kHz。12位A/D转换器的理想信噪比。此设计参数将用于确定抗混叠滤波器的顺序。本节中讨论的滤波器的例子是使用微芯片的滤波器实验室软件生成的。三个设计参数将用于实现适当的抗混叠滤波器：1。滤波器的截止频率必须为1kHz或更高。 2.滤波器在10kHz时衰减信号到-74dB。 3.模拟信号将只被滤波，而没有获得或反转。

用贝塞尔滤波器设计实现（Bessel）
在图13中使用了贝塞尔滤波器的设计来实现上述系统中的抗混叠滤波器。该实现需要一个截止频率为1kHz的第5阶滤波器。结合两个下降键滤波器加上一个无源低通滤波器，如图14所示。该滤波器将模拟输入信号79dB从通带区域衰减到10kHz。该贝塞尔五阶滤波器的频率响应如图13所示。


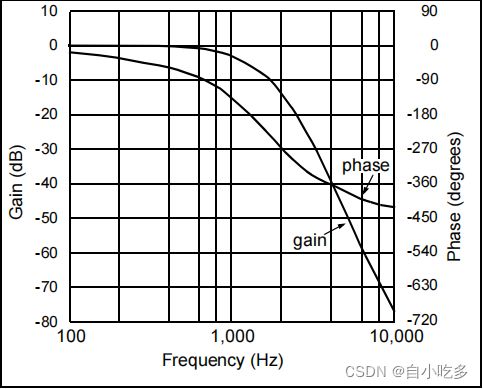
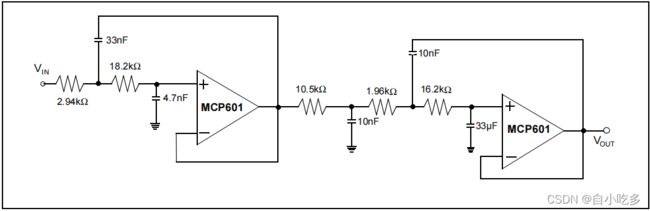
图14：五阶贝塞尔设计实现了两个有源滤波器和无源滤波器。该滤波器被设计为一种抗混叠滤波器，其截止频率为1kHz，停止频带频率为~5kHz。

用切比雪夫设计来实现
当使用切比雪夫滤波器设计在上述系统中实现抗混叠滤波器时，需要一个三阶滤波器，如图15所示。

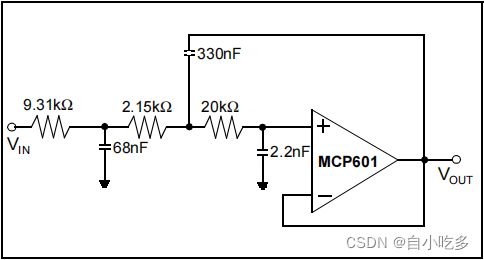
图15：使用一个有源滤波器和一个无源滤波器实现的三阶切比雪夫设计。该滤波器被设计为一种抗混叠滤波器，其截止频率为1kHz-4db的纹波，停止频带频率为~5kHz。

虽然该滤波器的阶数小于贝塞尔，但它在频率响应的通带部分有一个4dB的纹波。使用了一个有源滤波器和一个无源低通滤波器的组合。该滤波器在10kHz时衰减到-70dB。该切比雪夫三阶滤波器的频率响应如图16所示。

图16：在图15中实现的三阶切比雪夫设计的频率响应
该滤波器提供少于理想的74dB的动态范围(AMAX)，这应该被考虑在内

在12位系统中，-70dB和-74dB衰减之间的差异将引入略小于1/2的LSB误差。这是从10kHz到11.8KHz的混叠信号的结果。此外，在通频带中也会出现一个4dB的增益误差。这是通频带中的纹波响应的结果，如图16所示。

图17：四阶巴特沃斯设计实现了两个有源滤波器。该滤波器被设计为一种抗混叠滤波器，其截止频率为1kHz，停止频带频率为~5kHz。

用巴特沃斯设计来实现
作为最后一种替代方案，巴特沃斯滤波器设计可以用于抗混叠滤波器的滤波器实现，如图17所示。
对于这种电路的实现，使用了一个四阶滤波器，截止频率为1kHz。使用了两个有源键过滤器。该滤波器在10kHz处衰减通带信号80dB。该巴特沃斯四阶滤波器的频率响应如图18所示。

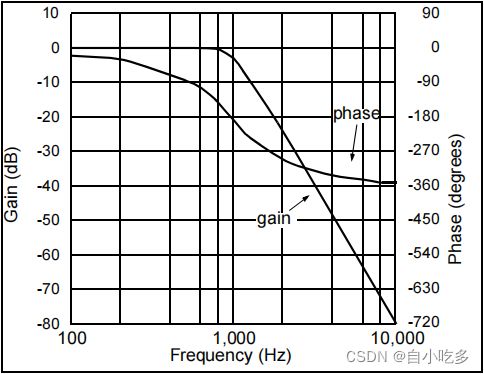
图18：在图17中实现的四阶巴特沃斯设计的频率响应。
表4总结了上述三个滤波器的频率响应以及其他几个选项。

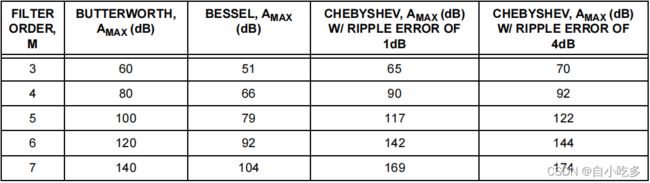
表4：不同滤波器设计与滤波器顺序之间的10kHz下的理论频率响应。每个滤波器的截止频率为1kHz。

结论
模拟滤波是数据采集系统的关键组成部分。如果不使用模拟滤波器，则将A/D转换器采样带宽一半之外的信号返回到信号路径中。在数字化过程中，一旦信号被锯齿，就不可能区分频带和带外的噪声。本应用说明讨论了如何确定和实现抗混叠滤波器的适当模拟滤波器设计参数的技术。