普通Trie树及相关应用

何为Trie

 Trie(字典树)是一种用于实现字符串快速检索的多叉树结构。$Trie$的每个节点都有若干个字符指针，若在插入或检索字符串时扫描到一个字符$c$，就沿着当前节点的$c$字符指针，走向该指针指向的节点，下面我们来详细讨论$Trie$的基本操作过程。

Trie的基本操作

初始化

 没啥好说的，就是空$Trie$只包含一个根节点，该点的字符指针指向空。

插入

 当我们需要插入一个字符串$S$时，我们令一个指针$P$起初指向根节点。然后，依次扫描$S$中的每个字符$c$：
 1.若$P$的$c$字符指针指向一个已经存在的节点$Q$，则令$P=Q$。
 2.若$P$的$c$字符指针指向空，则新建一个节点$Q$，令$p$的字符指针指向$Q$，然后令$P=Q$。
 总的来说，可以归纳为有则指向，无则新建再指向。
 同时，一旦$S$中的字符被扫描完毕后，需要在当前节点$P$上标记它是一个字符串的结尾。

检索

 当需要检索一个字符串$S$在$Trie$中是否存在时，我们令一个指针$P$起始指向根节点，然后依次扫描S中的每个字符$c$：
 1.若$P$的$c$字符指针指向空，则说明$S$没有被插入过$Trie$，结束检索。
 2.若$P$的$c$字符指针指向一个已经存在的节点$Q$，则令$P=Q$。
 当$S$中的字符扫描完毕后，若当前节点$P$被标记为一个字符串的末尾，则说明$S$在$Trie$中存在，否则说明$S$没有被插入过$Trie$。

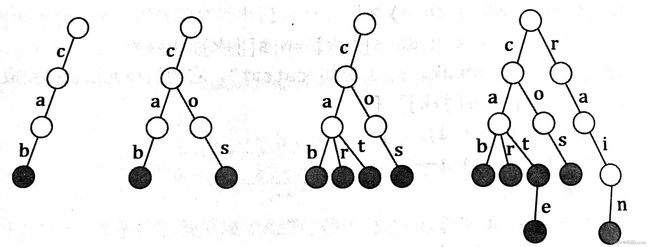
 上图取自于算法竞赛进阶指南一书，在上图的例子中，需要插入和检索的字符串都是由小写字母构成，所以$Trie$的每个节点具有$26$个字符指针，分别为$a$到$z$。上图展示了一棵空$Trie$中依次插入$“cab”“cos”“car”“cat”“cate”和“rain”$后的$Trie$形态，黑色部分标记了单词的末尾节点。
 可以看出在Trie中，字符数据都体现在树边上，树的节点仅保存了一些额外信息，例如单词的结尾标记等。其空间复杂度是$O(NC)$，其中的N是节点个数，C是字符集的大小。

Trie基本操作的代码实现

 建树即可，但要注意代码中的end操作判断字符串结尾

插入

int trie[MAXN][26],tot=1;
inline void insert(char* str){
	int len=strlen(str),p=1;
	for(int k=0;k<len;k++){
		int ch=str[k]-'a';
		if(trie[p][ch]==0)trie[p][ch]=++tot;
		p=trie[p][ch];
	}
	end[p]=true;
} 

检索

inline bool search(char* str){
	int len=strlen(str),p=1;
	for(int k=0;k<len;k++){
		p=trie[p][str[k]-'a'];
		if(!p)return false;
	}
	return end[p];
} 

实战练习

 【例题】前缀统计 传送门

 题目大意：一共有$T$组数据，每组数据给定$N$个字符串$S_1$,$S_2$,……,$S_N$。每组接下来进行$q$次询问，每次询问在给定一个字符串$S$，求$S_1$,$S_2$,……,$S_N$中有多少个字符串是$S$的前缀。
 题目分析：模板题，没啥好说的。在基本的$Trie$树基础上用$cnt$数组维护每个节点是多少个字符串的末尾节点，查询时只用返回待查询字符串的末尾字符对应节点的$cnt$值。
 代码如下

#include
#define MAXN 3000005
#define in read()
using namespace std;
int T,tot=1;
int trie[MAXN][65],cnt[MAXN];
char str[MAXN];
inline int getnum(char x){
	if(x>='A' and x<='Z')return x-'A';
	else if(x>='a' and x<='z')return x-'a'+26;
	else return x-'0'+52; 
}
inline int read(){
	int x=0,f=1;char c=getchar();
	while(c<'0' or c>'9'){if(c=='-')f=-1;c=getchar();}
	while(c>='0' and c<='9'){x=(x<<3)+(x<<1)+c-'0';c=getchar();}
	return x*f;
}
//inline void empty(){
//	memset(cnt,0,sizeof(cnt));
//	memset(trie,0,sizeof(trie));
//	tot=1;
//}
inline void insert(char* str){
	int len=strlen(str),p=1;
	for(int k=0;k<len;k++){
		int ch=getnum(str[k]);
		if(trie[p][ch]==0)trie[p][ch]=++tot;
		p=trie[p][ch];
		cnt[p]++;
	}
}
inline int search(char* str){
	int len=strlen(str),p=1;
	for(int k=0;k<len;k++){
		int ch=getnum(str[k]);
		p=trie[p][ch];
		if(!p)return 0;
	}
	return cnt[p];
}
int main(){
	T=in;
	for(int cas=1;cas<=T;cas++){
		int n=in,q=in;
		for(int i=0;i<=tot;i++)
            for(int j=0;j<=122;j++)
            	trie[i][j]=0;
        for(int i=0;i<=tot;i++)
            cnt[i]=0;
        tot=1;
		for(int i=1;i<=n;i++){
			scanf("%s",str); 
			insert(str);
		}
		for(int i=1;i<=q;i++){
			scanf("%s",str);
			cout<<search(str)<<'\n';
		}
		//empty();
	}
	return 0;
}