算法学习day18
文章目录
-
-
- 513.找树左下角的值
-
- 递归
- 迭代
- 112 .路径总和
-
- 递归
- 迭代
- 113.路径总和II
-
- 递归
- 106.从中序与后序遍历序列构造二叉树
-
- 递归
- 105.从前序与中序遍历序列构造二叉树
-
- 卡尔递归版本
- 递归优化
- 总结
-
513.找树左下角的值
给定一个二叉树的 根节点 root,请找出该二叉树的 最底层 最左边 节点的值。
假设二叉树中至少有一个节点。
示例 1:
输入: root = [2,1,3]
输出: 1
示例 2:
输入: [1,2,3,4,null,5,6,null,null,7]
输出: 7
提示:
- 二叉树的节点个数的范围是
[1,104] -231 <= Node.val <= 231 - 1
递归
利用最大深度,判断是否时最后一层,每次更新最大深度,不断更新左侧节点的返回值,第一个大于最大深度的一定是左下角的值
- 入参:根节点,递归深度
- 终止条件:无子节点,且当前深度大于最大深度
- 循环逻辑:迭代一层回溯一次
class Solution {
int maxDepth ,res ;
public int findBottomLeftValue(TreeNode root) {
maxDepth(root,1);
return res ;
}
public void maxDepth(TreeNode root,int depth) {
//终止条件,无子节点
if(root.left == null && root.right == null) {
//只有大于最大深度时才能更新最大深度,此时左右深度相同,第一个值就是左子树的值
if(depth > maxDepth) {
maxDepth = depth ;
res = root.val ;
return;
}
}
//单层循环逻辑
if(root.left!= null) {
depth++;
maxDepth(root.left,depth+1);
depth--;
}
if(root.right!= null) {
depth++;
maxDepth(root.right,depth+1);
depth--;
}
}
}
迭代
- 层序遍历,每层的第一个值
class Solution {
public int findBottomLeftValue(TreeNode root) {
Queue queue = new LinkedList<>();
queue.offer(root);
int res = root.val;
while (!queue.isEmpty()) {
int size = queue.size();
for (int i = 0; i < size; i++) {
TreeNode node = queue.poll();
//队列的第一个节点是左节点的值
if(i == 0){
res = node.val;
}
if (node.left!= null) {
queue.offer(node.left);
}
if (node.right!= null) {
queue.offer(node.right);
}
}
}
return res;
}
}
112 .路径总和
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
叶子节点 是指没有子节点的节点。
示例 1:
输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出:true
解释:等于目标和的根节点到叶节点路径如上图所示。
示例 2:
输入:root = [1,2,3], targetSum = 5
输出:false
解释:树中存在两条根节点到叶子节点的路径:
(1 --> 2): 和为 3
(1 --> 3): 和为 4
不存在 sum = 5 的根节点到叶子节点的路径。
示例 3:
输入:root = [], targetSum = 0
输出:false
解释:由于树是空的,所以不存在根节点到叶子节点的路径。
提示:
- 树中节点的数目在范围
[0, 5000]内 -1000 <= Node.val <= 1000-1000 <= targetSum <= 1000
递归
- 递归三部曲:入参和返回值(局部变量),终止条件,单层循环逻辑
- 入参:节点,路径、返回结果
- 终止条件:左右子节点为空,添加返回值
- 循环条件:每循环一层,递归+回溯
class Solution {
int sum = 0;
public boolean hasPathSum(TreeNode root, int targetSum) {
if(root == null) return false;
sum += root.val;
if(root.left == null && root.right == null) {
return sum == targetSum;
}
if(root.left!= null){
if(hasPathSum(root.left, targetSum)){
return true;
}
sum -= root.left.val;
}
if(root.right!= null){
if(hasPathSum(root.right, targetSum)){
return true;
}
sum -= root.right.val;
}
return false;
}
}
迭代
- 参考二叉树的层序先序,借助栈+回溯,类似于递归
113.路径总和II
给你二叉树的根节点 root 和一个整数目标和 targetSum ,找出所有 从根节点到叶子节点 路径总和等于给定目标和的路径。
叶子节点 是指没有子节点的节点。
示例 1:
输入:root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出:[[5,4,11,2],[5,8,4,5]]
示例 2:
输入:root = [1,2,3], targetSum = 5
输出:[]
示例 3:
输入:root = [1,2], targetSum = 0
输出:[]
提示:
- 树中节点总数在范围
[0, 5000]内 -1000 <= Node.val <= 1000-1000 <= targetSum <= 1000
递归
- 入参:每个节点,目标值,返回结果,路径
- 终止条件:sum == targetSum
- 循环逻辑:每次回溯的节点,为当前递归的那个节点(递归参数里的节点)
class Solution {
int sum = 0 ;
public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
List<List<Integer>> res = new ArrayList<>();
if (root == null) {
return res;
}
List<Integer> paths = new ArrayList<>();
dfs(root, targetSum, res, paths);
return res;
}
public void dfs(TreeNode root,int targetSum , List<List<Integer>> res, List<Integer> paths){
//终止条件
if (root == null) {
return;
}
sum += root.val;
paths.add(root.val);
if (root.left == null && root.right == null) {
if (sum == targetSum) {
res.add(new ArrayList<>(paths));
}
return;
}
if(root.left != null){
dfs(root.left,targetSum, res, paths);
sum -= root.left.val;
paths.remove(paths.size() - 1);
}
if(root.right!= null){
dfs(root.right,targetSum, res, paths);
sum -= root.right.val;
paths.remove(paths.size() - 1);
}
}
}
106.从中序与后序遍历序列构造二叉树
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
示例 1:
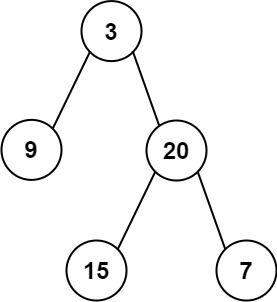
输入:inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出:[3,9,20,null,null,15,7]
示例 2:
输入:inorder = [-1], postorder = [-1]
输出:[-1]
递归
class Solution {
public TreeNode buildTree(int[] inorder, int[] postorder) {
//终止条件1
if (postorder.length == 0 || inorder.length == 0) {
return null;
}
//创建根节点
TreeNode root = new TreeNode(postorder[postorder.length - 1]);
//终止条件2
if (postorder.length == 1) {
return root;
}
//通过中序找到切割点index
int index = 0 ;
for (int i = 0; i < inorder.length; i++) {
if(inorder[i] == root.val) {
index = i ;
break;
}
}
//切中序数组 始终左闭右开
int[] leftInOrderSlice =subArray(inorder,0,index);
int[] rightInOrderSlice =subArray(inorder,index+1,inorder.length);
//切后序数组 以中序数组的左半部分的数组长度,切先序数组的左半部分
int[] leftPreSlice = subArray(postorder,0,leftInOrderSlice.length);
//切后序数组 以中序数组的右半部分的数组长度,切先序数组的右半部分
int[] rightPreSlice = subArray(postorder,leftPreSlice.length,leftPreSlice.length+rightInOrderSlice.length);
//创建左子树
root.left = buildTree(leftInOrderSlice,leftPreSlice);
//创建右子树
root.right = buildTree(rightInOrderSlice,rightPreSlice);
return root;
}
public int[] subArray(int[] array, int start, int end){
if(start>=end){
return new int[0];
}
int[] result = new int[end-start];
for (int i = start; i < end; i++) {
result[i-start] = array[i];
}
return result;
}
}
105.从前序与中序遍历序列构造二叉树
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
示例 1:
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
示例 2:
输入: preorder = [-1], inorder = [-1]
输出: [-1]
提示:
1 <= preorder.length <= 3000inorder.length == preorder.length-3000 <= preorder[i], inorder[i] <= 3000preorder和inorder均 无重复 元素inorder均出现在preorderpreorder保证 为二叉树的前序遍历序列inorder保证 为二叉树的中序遍历序列
卡尔递归版本
- 留个步骤
- 终止条件,任意数组为空
- 前序数组为1,结束遍历,返回根
- 使用前序数组的第一个节点,切割中序数组
- 分割中序数组的左右两部分
- 根据中序数组的左边部分的长度,分割前序数组,得到线序数组的左半部分和右边部分
- 递归给左右字数赋值
class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
//终止条件1
if (preorder.length == 0 || inorder.length == 0) {
return null;
}
//创建根节点
TreeNode root = new TreeNode(preorder[0]);
//终止条件2
if (preorder.length == 1) {
return root;
}
//通过中序找到切割点index
int index = 0 ;
for (int i = 0; i < inorder.length; i++) {
if(inorder[i] == root.val) {
index = i ;
break;
}
}
//切中序数组 始终左闭右开
int[] leftInOrderSlice =subArray(inorder,0,index);
int[] rightInOrderSlice =subArray(inorder,index+1,inorder.length);
//切前序数组 以中序数组的左半部分的数组长度,切先序数组的左半部分
int[] leftPreSlice = subArray(preorder,1,leftInOrderSlice.length+1);
//切后序数组 以中序数组的右半部分的数组长度,切先序数组的右半部分
int[] rightPreSlice = subArray(preorder,leftPreSlice.length+1,preorder.length);
//创建左子树
root.left = buildTree(leftPreSlice,leftInOrderSlice);
//创建右子树
root.right = buildTree(rightPreSlice,rightInOrderSlice);
return root;
}
public int[] subArray(int[] array, int start, int end){
if(start>=end){
return new int[0];
}
int[] result = new int[end-start];
for (int i = start; i < end; i++) {
result[i-start] = array[i];
}
return result;
}
}
递归优化
- 每次都是从原始数组的部分进行递归,可通过开始和结束下标,避免分割数组创建的临时数组,节省空间
class Solution {
Map<Integer, Integer> map = new HashMap<>();
public TreeNode buildTree(int[] preorder, int[] inorder) {
// 用map保存中序序列的数值对应位置
for (int i = 0; i < inorder.length; i++) {
map.put(inorder[i], i);
}
return findNode(preorder, 0, preorder.length, inorder, 0, inorder.length);
}
public TreeNode findNode(int[] preorder, int preBegin, int preEnd, int[] inorder, int inBegin, int inEnd) {
// 终止条件
if (preBegin >= preEnd || inBegin >= inEnd) {
return null;
}
// 单层循环逻辑:找到前序遍历的第一个元素在中序遍历中的位置
int rootIndex = map.get(preorder[preBegin]);
TreeNode root = new TreeNode(inorder[rootIndex]);
// 保存中序左子树个数,用来确定前序数列的个数
int lenOfLeft = rootIndex - inBegin;
root.left = findNode(preorder, preBegin + 1, preBegin + lenOfLeft + 1,
inorder, inBegin, rootIndex);
root.right = findNode(preorder, preBegin + lenOfLeft + 1, preEnd,
inorder, rootIndex + 1, inEnd);
return root;
}
}
总结
- 递归三部曲:参数和返回值、终止条件、单层循环逻辑
- 回溯要记录路径,一般用List记录所经过的path,回溯要和递归一起存在
- 先序+中序,后序+中序遍历的数组,可还原唯一一颗二叉树,先序+后序则无法确认左右顺序,无法还原唯一
- 还原二叉树,第一步找到根节点,在通过根节点切割中序、先序/后续,要梳理清楚切割的开始和结束位置