Customizable constraint systems for succinct arguments学习笔记（2）

微软研究中心Srinath Setty、a16z crypto research 和 Georgetown University Justin Thaler、Carnegie Mellon University Riad Wahby 20203年论文《Customizable constraint systems for succinct arguments》。

前序博客有：

• Customizable constraint systems for succinct arguments学习笔记（1）

4. SuperSpartan的Polynomial IOP for CCS

本节讨论的“SuperSpartan的Polynomial IOP for CCS”，为“Spartan [Set20] polynomial IOP for R1CS”的扩展。附录C中展示了如何扩展SuperSpartan的polynomial IOP来处理CCS+（即具有lookup操作的CCS）。

根据Definition 2.2，假定有某CCS structure-instance tuple with size bounds：
$((m,n,l,t,q,d),(M_0,\cdots ,M_{t-1},S_0,\cdots ,S_{q-1},x))$

为简便表示，令协议中的$m,n$均为powers of 2（若不是，则对每个矩阵$M_i$以及witness vector $z$进行补零，扩展$m,n$均为powers of 2，在以下SNARK协议中，并不会增加SNARK中的Prover time或Verifier time）。

将矩阵$M_0,\cdots ,M_{t-1}$解析为函数：$\{0,1{\}}^{\log m}\times \{0,1{\}}^{\log n}\to \mathbb{F}$。任何$\{0,1{\}}^{\log m}\times \{0,1{\}}^{\log n}$格式的输入都可解析为是索引$(i,j)\in \{0,1,\cdots ,m-1\}\times \{0,1,\cdots ,n-1\}$的二进制表示。该函数的输出为矩阵中第$(i,j)$个元素。

Spartan背景知识参见：

• 博客Spartan: zkSNARKS without trusted setup学习笔记
• 博客Spartan: zkSNARKS without trusted setup 源代码解析
• 博客Spartan中 Vitalik R1CS例子 SNARK证明基本思路

将Spartan中R1CS扩展为CCS表示：

Remark 10：

• Theorem 1中Prover runtime中的$O(qmd{\log }^{2}d)$项中包含了使用FFT来将$d$个不同的degree为1 的多项式相乘。FFT仅适于某些有限域。
  此外，实际的CCS/AIR/Plonkish instance，其$d$很少会超过100，通常低至5甚至是2 [GPR21, BGtRZt23]。因此，FFT的$O(d{\log }^{2}d)$ time要远远慢于 直接将$d$个degree为1的多项式相乘的$O(d^2)$ time。使用Karatsuba算法来代替FFT，也可获得sub-quadratic-in-$d$ time算法，且适于任何有限域。

Theorem 1证明：
对于某CCS structure和instance，$\mathcal{I}=(M_0,\cdots ,M_{t-1},S_0,\cdots ,S_{q-1},x)$和声称的witness $W$。令$Z=(W,1,x)$。
如之前所述，可：

• 将矩阵$M_0,\cdots ,M_{t-1}$解析为函数：$\{0,1{\}}^{\log m}\times \{0,1{\}}^{\log n}\to \mathbb{F}$。
• 将$Z$解析为函数：$\{0,1{\}}^{\log n}\to \mathbb{F}$。
• 将$(1,x)$解析为函数：$\{0,1{\}}^{\log n-1}\to \mathbb{F}$。【此时假设$Z$中witness $W$和$(1,x)$具有相同的长度$n/2$。】

函数$Z$的MLE $\tilde{Z}$表示为：
$tildeZ(X_0,\cdots ,X_{\log n-1})=(1-X_0)\cdot W(X_1,\cdots ,X_{\log n-1})+X_0\cdot (1,x)(X_1,\cdots ,X_{\log n-1})(13)$

可看出方程式（13）中的右侧为multilinear多项式。对于所有的$(x_0,\cdots ,x_{\log n-1})\in \{0,1{\}}^{\log n}$，很容易检查有$\tilde{Z}(x_0,\cdots ,x_{\log n-1})=Z((x_0,\cdots ,x_{\log n-1}))$。（因为$Z$ evaluations的前半部分对应$W$，后半部分对应vector $(1,x)$。）
因此方程式（13）中的右侧为$Z$的唯一multilinear extension。

若$(1,x)$长度小于$W$长度（如当根据Lemma 3将AIR转换为CCS）时，可对$x$填充补零获得$x_{pad}$，使其填充后$(1,x_{pad})$的长度与$W$一样。这样填充补零后，会让Verifier计算$(1,x)(X_1,\cdots ,X_{\log n-1})$的time增加$O(\log n)$次field加法运算。如，若未填充$(1,x)$长度为$2^l$，则很容易检查具有length为$n/2$的填充$(1,x_{pad})$的multilinear extension为：
$(X_1,\cdots ,X_{\log n-1})\to (1-X_{l+1})\cdot (1-X_{l+2})\cdots \cdot (1-X_{\log n-1}(1,x))(X_1,\cdots ,X_l)$

使得该multilinear多项式对于所有的inputs $(x_1,\cdots ,x_{\log n-1})$对应填充后的$(1,x_{pad})$，可认为其是填充后$(1,x_{pad})$的唯一multilinear多项式。

与Spartan论文Theorem 4.1类似，对由Spartan R1CS转换的CCS的“SuperSpartan的Polynomial IOP for CCS”协议为：

可对方程式（14）右侧的多项式应用sum-check协议：

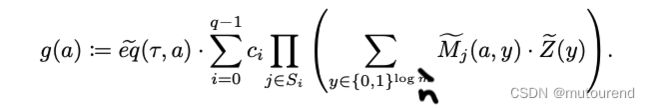
从Verifier的角度来看，这可将方程式（14）右侧的计算 reduce为 “evaluate $g$ at a random input $r_a\in {\mathbb{F}}^m$”。且Verifier 可自己以$O(\log m)$次field运算来计算$\widetilde{eq}(\tau ,r_a)$，因其易于检查：

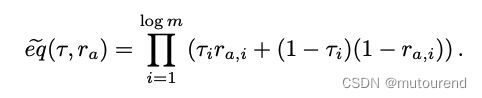
当Verifier计算出$\widetilde{eq}(\tau ,r_a)$值之后，Verifier计算$g(r_a)$的time为$O(dq)$。对于$i\in \{0,1,\cdots ,t-1\}$：

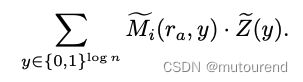
对该计算，可并行执行$t$个sum-check协议：为此，引入随机数$\gamma \in \mathbb{F}$，并对${\tilde{M}}_i(r_a,y)\cdot \tilde{Z}(y)$做random linear combination，权重分别为$[{\gamma }^0,\cdots ,{\gamma }^{t-1}]$。

在该sum-check协议中，Verifier在做final check时：仅需对以上$t$个多项式${\tilde{M}}_i(r_a,y)\cdot \tilde{Z}(y)$ evaluate at $r_y$，即意味着Verifier evaluate ${\tilde{M}}_i(r_a,r_y)$就足矣。这样的前提假设是Verifier具有query access to ${\tilde{M}}_0,\cdots ,{\tilde{M}}_{t-1}$，根据方程式（13），Verifier仅需对$\tilde{W}$和$(1,x)$各query一次就可获得$\tilde{Z}(r_y)$。

本文所实现的“SuperSpartan的Polynomial IOP for CCS”协议伪代码实现为：

总之，本文所实现的“SuperSpartan的Polynomial IOP for CCS”协议具有如下属性：

根据上面的“SuperSpartan的Polynomial IOP for CCS”协议伪代码可知，其包含了2次sum-check协议调用：

• 1）在3.a步骤中第一次触发sum-check协议时，Prover主要工作量为：
  
  
• 2）在3.c步骤中第二次调用sum-check协议，对应为$\log n$个变量的多项式：
  
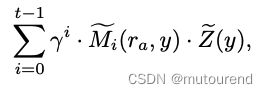
  其每个变量的degree最多为2。在sum-check协议中采用标准的linear-time-sum-check技术[CTY12, Tha13]，Prover的用时为$O(N+t)$。

5. 避免uniform IR中的预处理

当CCS instance中有“uniform” structure时（如某circuit具有多个相同的sub-circuit），为实现succinct verification cost，应避免对circuit structure的预处理。
对于uniform CCS instance，本文实现了：

• Verifier可evaluate the multilinear extension polynomials ${\tilde{M}}_0,\cdots ,{\tilde{M}}_{t-1}$ at any desired point in time logarithmic in the number of rows and columns of these matrices。

5.1 “adding 1 in binary”函数的multilinear extension

可将整数$\{0,1,\cdots ,D-1\}$的索引以二进制表示。整数$D-1$的索引可以全1向量表示，整数0索引可以全零向量表示。在这种索引表示法中，可将最右侧的bit看成是low-order bit。

对于某bit-vector $i\in \{0,1{\}}^{\log D}$，令$\text{to-int}(i)={\sum }_{j=0}^{\log D-1}{i}_j\cdot 2^j$对应$i$所表示的整数。对于整数$\kappa \in \{0,1,\cdots ,t-1\}$，$\text{bin}(\kappa )$表示$\kappa$对应的二进制表示。

定义函数：
$\text{next}(i,j):\{0,1{\}}^{\log D}\times \{0,1{\}}^{\log D}\to \{0,1\}$
其中：

• $i,j$为bit-vector输入
• 当且仅当整数$I=\text{to-int}(i)$和整数$J=\text{to-int}(j)$满足$J=I+1$时，该函数输出为1，否则为0。

因此可将该函数称为“adding 1 in binary”函数：

• 输入为2个bit-vector，判断第2个输入的整数 是否 为第1个输入整数加1。

注意：

• 若$i$为全1向量，则对于所有的$j\in \{0,1{\}}^{\log D}$，都有$(i,j)=0$。

从而有Theorem 2：

实际分析时分为3种情况：

接下来是解释方程式（16）可evaluate at any point $(r_x,r_y)\in {\mathbb{F}}^{\log D}\times {\mathbb{F}}^{\log D}$ in $O(\log D)$ time：

• 很容易看出$h(r_x,r_y)$可evaluate in $O(\log D)$ time。
• $g$中每个求和项可evaluate at $(r_x,r_y)$ in $O(\log D)$ time。
• $g$中共有$O(\log D)$个求和项，因此总的time bound 为$O(\log D^2)$。
• 不过，求和的相邻项中有几乎相同的因子，该runtime可reduce为$O(\log m)$。如，若$v(k)$为求和中的第$k$项，则：
  
  

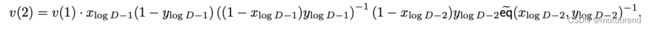
5.2 由AIR转换来的CCS

本小节中，$m$表示AIR的参数，有$w_{AIR}\in {\mathbb{F}}^{(m-1)\cdot t/2}，z_{AIR}\in {\mathbb{F}}^{(m+1)\cdot t/2}$。同时$m$表示CCS矩阵$M_0,\cdots ,M_{t-1}$的行数。本节还假设$m-1$为a power of 2，同时对$M_0,\cdots ,M_{t-1}$填充补零，使得其行数为a power of 2（该填充不会增加SuperSpartan中的Verifier或Prover time）。即意味着填充后的$M_0,\cdots ,M_{t-1}$的行数不再为$m$，而是$2(m-1)$。
这样处理便于基于实际域做实现，并借助上一节的 “adding 1 in binary”函数的multilinear extension，对由AIR转换来的CCS实际表达做了进一步优化。

5.3 避免SIMD CCS中的预处理

6. 将Polynomial IOP for CCS编译为SNARK for CCS