【多目标优化算法】自适应粒子群算法APSO，2009

自适应粒子群算法（APSO）

算法

PSO算法面临的两个最大的问题是收敛的速度和陷入局部最小值。针对此种情况，詹志辉教授基于标准的PSO提出了三个方式进行改进，分别是进化状态评估（ESE）、系统自适应参数（惯性权重、局部和全局加速度）和精英学习策略（ELS）。下面分别从这三个方面来介绍详细算法。

1. 进化状态评估（ELS）

ELS目的是为了收敛的状态进行评估和划分，为后面自适应参数提供基础。
step1: 计算每个粒子$i$的相对于其他粒子的平均距离（欧式距离）
$$d_i=\frac{1}{N-1}\sum _{j=1;j̸=i}^N\sqrt{\sum _{k=1}^D(x_i^k-x_j^k{)}^2}$$
其中N是种群的大小，D为问题的维数。
step2: 选出$d_i$中最好的值为$d_g$，计算$d_i$中最大距离为$d_{max}$，最小距离为$d_{min}$，计算进化因子$f$。
$$f=\frac{d_g-d_{min}}{d_{max}-d_{min}}\in [0,1]$$
step3: 根据上面计算的$f$，使用是隶属函数判断进化此刻的状态。其中四个状态分别是S1：探索（Exploration）、S2:发现（Exploitation）、S3:收敛（Convergence）、S4:跳出（Jumping Out）。
S1:
$$\mu s_1(f)=\{\begin{array}{ll}0，& 0\le f\le 0.4\\ 5\times f-2,& 0.4<f\le 0.6\\ 1,& 0.6<f\le 0.7\\ -10\times f+8,& 0.7<f\le 0.8\\ 0,& 0.8<f\le 1\end{array}$$
S2:
$$\mu s_2(f)=\{\begin{array}{ll}0，& 0\le f\le 0.2\\ 10\times f-2,& 0.2<f\le 0.3\\ 1,& 0.3<f\le 0.4\\ -5\times f+3,& 0.4<f\le 0.6\\ 0,& 0.6<f\le 1\end{array}$$
S3:
$$\mu s_3(f)=\{\begin{array}{ll}1，& 0\le f\le 0.1\\ -5\times f+1.5,& 0.1<f\le 0.3\\ 0,& 0.3<f\le 1\end{array}$$
S4:
$$\mu s_4(f)=\{\begin{array}{ll}0，& 0\le f\le 0.7\\ -5\times f-3.5,& 0.7<f\le 0.9\\ 1,& 0.9<f\le 1\end{array}$$

上图为根据隶属度函数划分的状态，可以清晰看出各个状态区域，但是各个状态之间有重合的区域，为了解决决定$f$的最终归属状态，在此使用了“singleton”方法。
在没有规则基准（rule base）的情况下：如果$f=0.45$，可参考上图中的红线，$\mu s_2(f)>\mu s_1(f)$，所以$f$属于$S_2$状态。
在有规则基准（rule base）的情况下：

• 在上述$S_1$和$S_2$的选择中，如果前一个状态是$S_4$，则$f$的状态属于$S_1$，根据规则基准的去模糊化得出。
• 如果上一个状态是$S_1$，由于不能过度切换状态，保持划分的稳定性，所以$f$属于仍然属于$S_1$状态。
• 如果上一个状态是$S_2$或者$S_3$，使用“singleton”方法结合上述的规则基准会将$f$划分到$S_2$状态。
  上述中有规则基准的情况是全文中描述最模棱两可的部分。根据我的理解，规则基准（rule base）实质上是状态转换的PSO序列$S_1=>S_2=>S_3=>S_4=>S_1...$。

2. 系统自适应参数（w、c1、c2）

• 惯性权重w自适应：
  惯性权重是PSO算法中平衡全局和局部的搜索能力，$w$应该在探索阶段很大，而在开发阶段减小。$w$不是单纯的随着时间变化的，而应该随着进化状态的而变化，故$w$应该与进化因子$f$有如下的关系：
  $$w(f)=\frac{1}{1+1.5e^{-2.6f}}\in [0.4,0.9]\forall f\in [0,1]$$
  本文中$w$初始化设定是0.9，在跳出状态和探索状态下，较大的$f$和较大的$w$更有利于全局搜索，相反在开发状态和收敛状态下$f$较小，$w$会减小更有利于局部的搜索。
• 加速因子的控制：
  参数$C_1$是“个体认知”，促进该粒子获得它历史上最好的位置，有利于开发局部中最好的解，增加粒子群的多样性。
  参数$C_2$是“社会认知”，它能推进粒子向全局中最好的区域收敛，加快收敛速度。
  
  
  本文中$C_1$和$C_2$的初始化都为2.0，这两个参数也是根据进化状态来进行控制的：
  策略1——在探索状态增加$C_1$，减小$C_2$：能帮助粒子探索自身的最好个体，强调个体认知的过程，避免粒子过早聚集在最好粒子周围，陷入局部最优。
  策略2——在开发状态轻微增加$C_1$，轻微减小$C_2$：这个状态下，粒子使用局部信息，种群朝着可能的局部最优区域移动，因此，轻微增加$C_1$可以使$C_1$维持在一个较大的值，可以强调在$pBes{t}_i$（个体最优）周围的搜索和开发。全局最优的粒子$gBes{t}_i$并不一定在这个状态处在真正的最优区域。所以轻微减小$C_2$可避免算法过早收敛，陷入局部最优值。
  策略3——在收敛状态轻微增加$C_1$，轻微增加$C_2$：在收敛状态下，群体似乎找到了全局的最优区域，因此，增加$C_2$主要为了引领其他粒子向可能的全局最优区域移动。此时$C_1$的值应该减小，这样有利于加来算法的收敛，但是使用12个基准函数显示，这样的策略会使两个参数过早的到值达上下边界（会在下文中介绍边界的大小定义）。这样可能会出现一种情况：即局部最优区域被当成全局最优区域，迅速收敛，最终陷入局部最优解。所以在此状态下，应该对$C_1$和$C_2$都进行轻微的增加。
  策略4——在跳出状态减小$C_1$，增加$C_2$：全局最优粒子$gBes{t}_i$跳出局部最优，远离原来的聚类，跳向更优的区域。此时原来聚类的粒子会紧随这个领导者，尽可能快的飞向这个粒子的周围，所以一个值较大的$C_2$和较小的$C_1$可以获得这个结果。
  
  
  关于加速度因子的上下边界：
  为了使每一代中$C_1$和$C_2$和上一代的值变化不太突兀，所以引入了一个参数“加速度率”$\delta$，上一代的加速度减这一代的加速度绝对值不超过$\delta$
  $$|c_i(g+1)-c_i(g)|\le \delta ,i=1,2.$$
  实验显示$\delta$的值做好从$[0.05,0.1]$间隔中随机产生。我们使用$0.5\delta$表示策略2和策略3中的“轻微改变”。如果$C_1$h和$C_2$的和超过了$4.0$则进行如下的归一化处理
  $$c_i=\frac{c_i}{c_1+c_2}4.0,i=1,2.$$
  下面是使用ESE来动态变化$w$和$c_1$和$c_2$部分的算法流程图
  

3. 精英学习策略（ELS）

在实验中的有些情况下，单纯使用ESE来动态更新$w$和$c_1$和$c_2$，出现了算法不收敛的情况下，因此ELS是用于帮助全局最优粒子$gBest$在收敛状态时跳出局部最优区域。推进$gBest$向着一个潜在最好区域前进。
ELS选择了目标问题的其中一个维度进行变化，从统计学上意义来说，对于每一个维度选择的概率都是相同的，选择其中的第$d$个维度，加入高斯扰动，过程如下：
$$P^d=P^d+(X_{max}^d-X_{min}^d)\cdot Gaussian(\mu ,{\sigma }^2)$$
其中$\sigma$是“精英学习率”，随着进化的代数而变化
$$\sigma ={\sigma }_{max}-({\sigma }_{max}-{\sigma }_{min})\frac{g}{G}$$
其中${\sigma }_{max}$和${\sigma }_{min}$的上界和下界根据经验显示${\sigma }_{max}=1.0$、${\sigma }_{min}=0.1$
降低SD值，在算法早期阶段中，提供一个较高的学习率，为了算法跳出可能的局部最优值。
在后期阶段中，较小的学习率可以引导$gBest$找到最终的最优解
ELS的流程图如下所示：

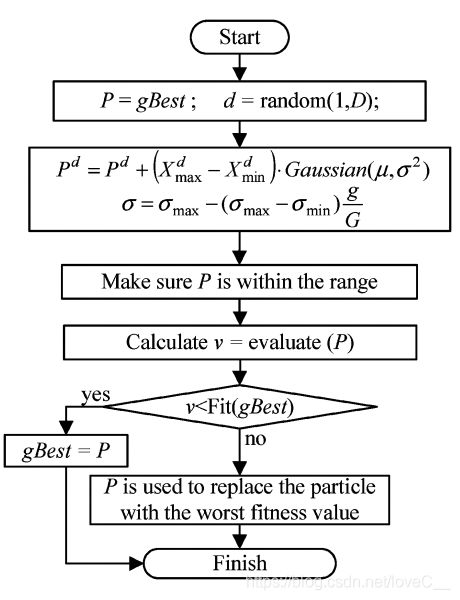
如果改变后的P适应度符合精度标准，则将P的值赋给$gBest$，否则则用P的值去代替种群中的最差例子。
整个算法的流程图：

与标准的PSO对比，APSO算法只在初始化之后得第二步与PSO不同，在第二步中算法加入了通过ESE动态更新$w$、$c_1$、$c_2$方法和ELS策略。
该算法在单峰函数和多峰函数中，大多表现优秀，且未占用过多的时间。由于免费午餐理论，一个算法无法在各个方面都保持最好的结果。