从RRT到RRT*，再到Informed RRT*，路径规划算法怎么写

做个正直的人

RRT中文名字是“快速搜索随机树”（Rapidly-exploring Random Tree），是一种比较常用的基于采样的静态路径规划算法。

我们可以这么理解：小明住在北京，小红住在南京，有一天小红给小明发了一条短信，短信上说只要小明从北京来南京见小红，小红就做小明的女朋友。单身青年小明一看给激动坏了，当即收拾东西要来南京。

1、RRT算法

1.1 假设

为了说明RRT算法，我们作出如下假设：

• 小明不知道从北京直达南京的路线；

• 在每一个城市，只能够获得到达相邻城市的路线，而不能到达不相邻的城市；

• 小明看不懂地图，只有一个列出了中国所有城市的城市清单。

1.2 RRT算法步骤与实现

小明的舍友甲为小明提出了一种找到从北京到达南京的算法——RRT算法。
小明只能拿着这个清单，重复如下过程：

    （1）随机选择一个城市，
    （2）看看这个城市是不是可达，
    （3）离南京（目标位置）多远，如果到达目标位置就终止算法
    （4）在已经选择过得城市中哪一个离它最近，就把那个城市设置为他的父节点。

不断的重复这个过程，这一个随机树就会不断的生长，直到到达目标位置。从下图可以看出经过许许多多次随机选择之后，目标城市就会变成这个随机树的叶节点，也就是说，小明就能找到一条从北京到南京的可行路径（仅仅是可行而已，很大概率上不会是最优）。

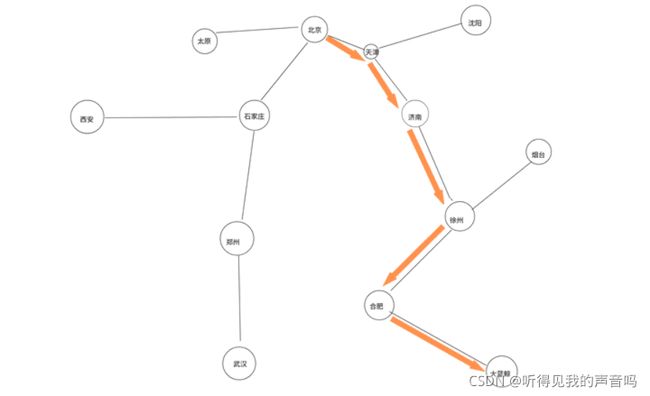
比如上面这幅图就是小明使用RRT算法找到的一条从北京到南京的路线。

1.3 伪代码

我们可以把RRT算法用伪代码的形式写出来，我认为伪代码用英语描述能够更加准确精炼的表达算法的步骤和精髓，所以我用英语来写伪代码：

//RRT算法伪代码——作者黄唐，2021.4.9于南京//initialization
Obtain map, 0 stands for free space and 1 obstacle.
Set start and goal in this map .
Set step_size which means how long we will search from the closest pos to the 
random pos obtained from sampling.(Why we need to set a step_size? Because the sample may be far away from our tree and we don't want to produce a very long edge.)
Set max iteration that means how many times we crop our tree.
Set current iteration as 0.
Set a flag which flags whether we have reached the goal.
Set goal_radius, if the distance from new_point to the goal is less than. 
goal_radius we think we have reached the goal.
If we don't set this goal_radius we may never reach the goal because the 
probability that we sample the goal is 0.
//make plan
We need a vector to memorize the position the we have detected
Push the start into the vector and set its parent as -1 and its index 0 which 
means it is the root of our tree while(we haven't reached the goal and the max iteration){
    Sample in the map and get a random pos as random_point
    Get the closest pos as closest_point in the vector(tree) whose distance to 
    random_point is min among all members in the vector
    Move from the closest_point to the random_point and produce a new point as 
    new_point in this edge whose distance to closest_point is step_size 
    if (the edge from closest_point to new_point is safe which means there is no 
        collision with any obstacle){
        Push the new_point into the vector and set its parent as closest_point
        current iteration ++
        if (the distance from new_point to goal < goal_radius){
            if (the edge from new_point to goal is safe){
                flag =true
                Set new_point as parent of the goal
            }
        }
        //RRT*算法的rewrite和relink写在这里哟
     }
     else{
        Abandon this sample and continue
     }
} 
return the index of new_point as the parent of the goal


//build plan 
if (the index of parent of the goal>=0){
    push the goal at the front of the path 
    current_parent =the index of parent of the goal
     while(the index of current_parent>0){
        Push the current_parent at the front of the path
        current_parent= index of parent of current_parent
     }
    Push start at the front of the path
    return path
}
else {
    We can't obtain a path from start to goal
    return -1
}

懒得看英语的可以直接看中文的伪代码：

//初始化
拿到一幅地图，0表示自由移动的空间，1表示障碍物
设定初始位置start和目标位置goal
设定生长步长step_size，为什么要设置这么个东西呢？比如说采样点离我们现有的树实在是太远了，直接把这
一个点加入到树中就会产生一条特别长的边，我们可不想有这么长的边
设定一个标志flag，如果我们到达了目标位置就设置它为true，我们就终止循环，不再继续搜索路径
设置一个变量goal_radius来形成一个以goal为圆心，goal_radius为半径的圆（三维空间就是球，更高维就
是超球），因为如果我们不设置这个东西，我们的算法可能永远也不会找到到达目标的路径，因为在平面上采样到
一个点的概率是0。
 
//makeplan
声明一个向量vector来存储我们的树中当前有哪些节点，以及这些节点的位置、索引和父节点
把起始位置压入vector中作为RRT的根节点
把目标位置的父节点索引parent_of_goal设置为-1
while(flag!=true && 未达到最大迭代次数){
    随机采样一个点作为random_point
    遍历RRT（也就是vector）找到距离采样点最近的那个节点，记为closest_point
    从closest_point向random_point搜索step_size距离，将这一点记为new_point
    检查从closest_point到new_point这一段路径是不是安全，也就是会不会哈障碍物发生碰撞
    if(不会发生碰撞){
        将这一个新节点new_point压入到RRT中，并将他的父节点设置为closest_point
        迭代次数++
        检查这一个新节点是不是位于以goal为圆心的圆内
        if(在圆内){
            检查new_point到goal是不是安全
            if(安全){
                设置flag为true，表示我们到达目标区域了
                设置parent_of_goal为new_point的索引
            }
            else{
                do nothing
            }
        }
        //RRT*的rewrite和relink写在这里哟
    }
    else{
        不安全，舍弃这一个点，从新采样
    }
}
return parent_of_goal
 
//生成路径
if(parent_of_goal >0){
    从goal不断的向父节点回溯，直到回到根节点，也就是start，这一条回溯路径就是RRT算法找到的路径
}
else{
    没有找到路径，失败
}

2、RRT*算法

小明的舍友乙指出，甲的RRT算法找到的路径并不够优秀，舍友乙对舍友甲的算法作出了改进，提出了一种RRT*算法。

下面讲讲RRT*算法。加了个*，很明显这是对RRT的一种改进，就像A算法和A*算法一样。从前面那副图中我们可以看出来RRT只能找出一条可行路径，并不能保证找到一条最优路径，换句话说，RRT会让小明走很多弯路，这会让小明更晚收获他的爱情。所以乙提出了一种RRT*算法。RRT*算法在RRT算法的基础上增加了两步：rewrite 和random relink。也就是重写和随机重连。

先解释一下什么是重写，什么是重连。

重写就是，在新节点new_point加入到树中之后，重新为它选择父节点，好让它到起始点的路径长度（代价）更小。

随机重连是在重写完成之后，对新节点new_point附近一定范围内的节点进行重连。重连就是，检查一下如果把new_point附近的这些节点的父节点设置为new_point，这些节点的代价会不会减小。如果能够减小，就把这些节点的父节点更改为new_point；否则，就不更改。
(论文的作者已经证明RRT*算法是一种渐进最优的算法，也就是说当时间趋于无穷大的时候，这个算法就能够找到最优的路径。)

由于RRT算法不考虑距离，RRT*算法考虑每一个节点到出发点的距离，为此每一个节点会增加一个属性：distance_to_start，即到出发点的距离。相应的在为每一个节点选择父节点的时候，新节点的距离等于父节点的距离加上父节点到子节点的直线距离，即：
$$child.distance\_to\_start=parent.distance\_to\_start+getDistance(parent,child)$$
原本RRT的代码不用更改，只需要把rewrite和random relink 加进去就可以。
rewrite重写的伪代码如下所示：

遍历整个树，
获得到新节点new_point的距离小于一定阈值（比如1.5倍的步长，也就是1.5*step_size）的所有节点
将这些节点加入到一个名为candidate_parent_of_newpoint的列表中，
为了方便，这些节点的distance不再用来存储到出发点的距离，而是用来存储如果把该节点设置为newpointt
的父节点的话，newpoint到出发点的距离。
找到candidate_parent_of_newpoint列表中具有最小distance的那个节点，返回他的索引index，
将新节点newpoint的父节点设置为index。

random relink的伪代码如下所示：

遍历整个列表，对每一个节点执行如下动作{
  if(该节点到newpoint的距离小于一定的阈值，比如1.6倍的步长，也就是1.6*step_size){
    if（该节点现在的distance>把该节点的父节点更新为newpoint之后的distance){
        把该节点的父节点设置为newpoint，并更新该节点的distance值
        更新以该节点为根节点的子树中的每个节点的distance。我用队列结构实现了一个，但是算法效率很低，
        正在想办法改进。
    }
  }
  else{
    do nothing
  }
}

3、Informed RRT*算法

使用了这个RRT*算法之后，小明发现找到的路径明显变得优秀多了。但是室友丙这时候站出来说话了，他说，RRT*算法是找到了一条更优的路径，但是它的计算量太大了，导致算法的效率比较低，我给改进了一下。舍友丙提出了Informed RRT*算法。

Informed RRT*顾名思义，是加入了一些已经informed的信息。实际上informed RRT的思路非常简单，它仅仅是对RRT和RRT*的采样函数做了一些限制。在没有搜索到任何一条可达路径之前，informed RRT*算法就是RRT*算法，在找到了一条可达路径之后，informed 就不再采用原来的采样函数，而是采用一个椭圆采样函数。

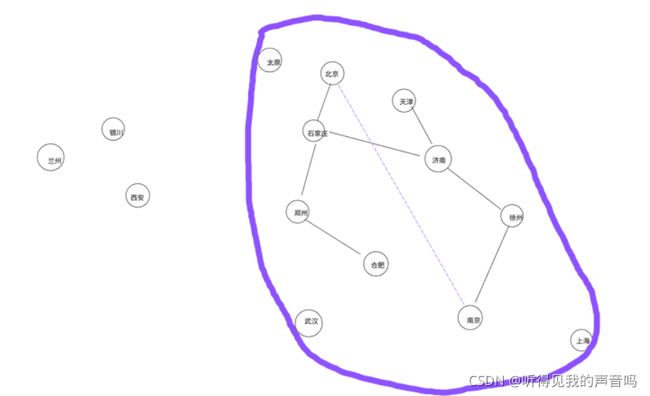
我们假定上图中的蓝色线是一个非常非常标准的椭圆。
假设目前已经找到一个可达的路径：北京——石家庄——济南——徐州——南京。但是这时候，informed RRT*算法并不会终止，而是会在这一条路径的基础上进行优化。

informed RRT*的做法是，在找到一条可达路径之后，把这一条路径的长度作为cMax，把出发点和目标点之间的距离作为cMin。这样做的目的就是，构造一个椭圆出来，把出发点和目标点作为椭圆的两个焦点F1和F2，这一条可达路径的长度做作为2a。因为我们知道，椭圆上的点P满足如下关系：
$$|PF1|+|PF2|=2a$$
此后我们就只在这一个椭圆内部采样，而不会再去椭圆外部采样。因为很明显，我已经找到了一个可行路径，比如上图中的路径，那么这个时候，我再去采样西安或者兰州，并不会对我现有路径的优化产生什么作用，除了增大计算量以外。该算法每发现一个更小的cMax就会更新一次cMax，直到cMax满足一定的条件或者达到最大迭代次数才会终止。比如当 $$cMax<1.2cMin$$ 时终止算法。
乍一看，这个改进似乎没什么了不起的，仅仅是优化了一下采样函数而已嘛。但是这仅仅是在二维空间中进行采样而已，当遇到更高维问题比如六自由度的机械臂的运动规划是在六维空间中，一般的移动机械臂甚至可以达到12个自由度，这种时候，对采样空间进行限制带来的好处是巨大的。
就这样，小明在三位热心舍友的帮助下成功的找打了一条非常不错的去南京的路线，不知道小明会不会如愿以偿呀？
关于如何在该椭圆内部采样，其实可以用坐标变换的方法，在单位圆内采样是很容易实现的，然后把该采样点通过坐标变换变换到椭圆内就可以了。