计算机图像处理—HOG 特征提取算法

一、实验介绍

1. 实验内容

本实验将学习HOG 特征提取算法。

2. 实验要点

• HOG 算法
• HOG 算法有效的原因
• 创建 HOG 描述符
• HOG 描述符中的元素数量
• 可视化 HOG 描述符
• 理解直方图

3. 实验环境

• Python 3.6.6
• numpy
• matplotlib
• cv2
• copy

二、实验步骤

简介

正如在 ORB 算法中看到的，我们可以使用图像中的关键点进行匹配，以检测图像中的对象。当想要检测具有许多一致的内部特性且不受背景影响的对象时，这些类型的算法非常有用。例如，这些算法在人脸检测中可以取得良好的效果，因为人脸有许多不受图像背景影响的一致的内部特征，例如眼睛、鼻子和嘴巴。然而，当试图进行更一般的对象识别时，例如图像中的行人检测时，这些类型的算法并不能很好地工作。原因是人们的内在特征不像脸那样一致，因为每个人的体型和风格都不同（见下图）。这意味着每个人都会有一套不同的内部特征，因此我们需要一些能够更全面地描述一个人的东西。

Fig. 1. - Pedestrians.

一种选择是尝试通过行人的轮廓来检测他们。通过图像的轮廓（边界）来检测物体是非常具有挑战性的，因为我们必须处理背景和前景之间的对比带来的困难。例如，假设想检测一个图像中的行人，她正走在一栋白色建筑前，穿着白色外套和黑色裤子。我们可以在下图中看到，由于图像的背景大多是白色，黑色裤子的对比度将非常高，但由于外套也是白色的，所以对比度将非常低。 在这种情况下，检测裤子的边缘是很容易的，但是检测外套的边缘是非常困难的。而这就是为什么需要HOG。即定向梯度柱状图（Histograms of Oriented Gradients），它是由 Navneet Dalal 和 Bill Triggs 于 2005 年首次引入的。

Fig. 2. - High and Low Contrast.

Hog 算法的工作原理是创建图像中梯度方向分布的柱状图，然后以一种非常特殊的方式对其进行归一化。这种特殊的归一化使得Hog 能够有效地检测物体的边缘，即使在对比度很低的情况下也是如此。这些标准化的柱状图被放在一个特征向量（称为 HOG 描述符）中，可以用来训练机器学习算法，例如支持向量机（SVM），以根据图像中的边界（边）检测对象。由于它的巨大成功和可靠性，HOG 已成为计算机视觉中应用最广泛的目标检测算法之一。

在本次教程中，将要讲到的内容有：

• HOG 算法的工作原理
• 如何使用 OpenCV 创建一个 HOG 描述符
• 如何可视化 HOG 描述符

1 HOG 算法

顾名思义，HOG 算法基于从图像梯度方向创建直方图。HOG算法通过以下一系列步骤实现：

1. 计算检测窗口中每个像素的梯度大小和方向。

2. 计算检测窗口中每个像素的梯度大小和方向。

3. 将检测窗口分成像素的连接单元格，所有单元格的大小相同（见下图）。单元的大小是一个自由参数，通常选择它来匹配要检测的特征的比例。例如，在一个 64 x 128 像素的检测窗口中，6 到 8 像素宽的方形单元适用于检测人体肢体。

4. 为每个单元创建一个柱状图，首先将每个单元中所有像素的渐变方向分组为特定数量的方向（角度）箱，然后将每个角度箱中渐变的渐变幅度相加（见下图）。柱状图中的箱数是一个自由参数，通常设置为9个角箱。

5. 将相邻单元分组成块（见下图）。每个块中的单元格数是一个自由参数，所有块的大小都必须相同。每个块之间的距离（称为跨距）是一个自由参数，但它通常设置为块大小的一半，在这种情况下，将得到重叠块（见动图）。经验表明，该算法能更好地处理重叠块。

6. 使用每个块中包含的单元格来规范化该块中的单元格柱状图（见下图）。如果有重叠的块，这意味着大多数单元格将针对不同的块进行规格化（见动图）。因此，同一个单元可能有几个不同的归一化

7. 将所有块中的所有标准化柱状图收集到一个称为 HOG 描述符的特征向量中

8. 使用从包含同一对象的许多图像中得到的 HOG 描述符训练机器学习算法，例如使用 SVM，以检测图像中的这些对象。例如，可以使用来自许多行人图像的 HOG 描述符来训练 SVM 以检测图像中的行人。训练通过使用包含目标的正例和不包含目标的负例完成。

9. 一旦对支持向量机进行了训练，就使用滑动窗口方法来尝试检测和定位图像中的对象。检测图像中的对象需要找到图像中与 SVM 学习到的 HOG 模式相似的部分。

Fig. 3. - HOG Diagram.
Vid. 1. - HOG Animation.

2 为什么 HOG 算法有效

正如我们上面所了解的，HOG 通过在图像的局部区域中添加特定方向的梯度大小来创建柱状图，称为“cells”。通过这样做可以保证更强的梯度对它们各自的角度柱状图的大小贡献更大，同时最小化由噪声引起的弱梯度和随机定向梯度的影响。通过这种方式，柱状图告诉我们每个单元格的主要梯度方向。

2.1 处理相对性问题

现在考虑一个问题，由于局部照明的变化以及背景和前景之间的对比度，梯度方向的大小可以有很大的变化。

为了考虑背景-前景对比度的差异，HOG 算法尝试在局部检测边缘。为了做到这一点，它定义了称为块的单元格组，并使用该局部单元格组规范化柱状图。通过局部归一化，HOG 算法可以非常可靠地检测每个块中的边缘，这称为块归一化。

除了使用块规范化之外，HOG 算法还使用重叠块来提高其性能。通过使用重叠块，每个单元为最终的 HOG 描述符提供几个独立的组成部分，其中每个组成部分对应于一个针对不同块进行规范化的单元。这似乎是多余的，但是经验表明，通过对每个单元对不同的局部块进行多次规格化，HOG 算法的性能显著提高。

加载图像和导入资源

构建HOG描述符的第一步是将所需的软件包加载到Python中并加载我们的图像。

我们首先使用OpenCV加载三角形图块的图像。 由于cv2.imread（）函数将图像加载为BGR，因此我们会将图像转换为RGB，以便可以使用正确的颜色进行显示。 与往常一样，我们会将BGR图像转换为灰度进行分析。

import cv2
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

# 设置默认图形的尺寸
plt.rcParams['figure.figsize'] = [17.0, 7.0]

# 载入图片 
image = cv2.imread('./images/triangle_tile.jpeg')

# 将原始图像转换为RGB
original_image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)

# 将原始图像转换为灰度
gray_image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)

# 输出原始图像和灰度图像的形状
print('The original image has shape: ', original_image.shape)
print('The gray scale image has shape: ', gray_image.shape)

# 输出图像
plt.subplot(121)
plt.imshow(original_image)
plt.title('Original Image')
plt.subplot(122)
plt.imshow(gray_image, cmap='gray')
plt.title('Gray Scale Image')
plt.show()

The original image has shape:  (250, 250, 3)
The gray scale image has shape:  (250, 250)

3 创建 HOG 描述符

我们将使用 OpenCV 的HOGDescriptor类来创建 HOG 描述符。HOG 描述符的参数是使用HOGDescriptor() function. The parameters of the HOGDescriptor() 函数设置的。 HOGDescriptor() 函数的参数及其默认值如下：

cv2.HOGDescriptor(win_size = (64, 128), block_size = (16, 16), block_stride = (8, 8), cell_size = (8, 8), nbins = 9, win_sigma = DEFAULT_WIN_SIGMA, threshold_L2hys = 0.2, gamma_correction = true, nlevels = DEFAULT_NLEVELS)

官方参数解释如下:

• win_size – Size
  检测窗口的大小，以像素为单位（宽度，高度）。 定义感兴趣的区域。 必须是像素大小的整数倍。

• block_size – Size
  块大小，以像素为单位（宽度，高度）。 定义每个块中有多少个单元格。 必须是像素大小的整数倍，并且必须小于检测窗口。 方块越小，可以获得的细节越细。

• block_stride – Size 块的步幅
  块跨度以像素为单位（水平，垂直）。 它必须是像元大小的整数倍。 block_stride定义相邻块之间的距离，例如，水平8个像素，垂直8个像素。 较长的block_strides使算法运行更快（因为评估的块更少），但是算法的效果可能不佳。

• cell_size – Size
  像元大小（以像素为单位）（宽度，高度）。 确定单元格的大小。 单元格越小，可以获得的细节越精细。

• nbins – int 直方图的条数(bins)
  直方图的箱数。确定用于制作直方图的角度仓的数量。使用更多箱柜，您可以捕获更多梯度方向。 HOG使用无符号的渐变，因此角度单元的值将介于0和180度之间。

• win_sigma – double
  高斯平滑窗口参数。 通过在计算直方图之前对每个像素应用高斯空间窗口，可以对块边缘附近的像素进行平滑处理，从而提高HOG算法的性能。

• threshold_L2hys – double
  L2-Hys（Lowe样式修剪的L2范数）归一化方法收缩。 L2-Hys方法用于对块进行规范化，它由L2范数，裁剪和重新规范化组成。 限幅将每个块的描述符向量的最大值限制为具有给定阈值的值（默认为0.2）。 裁剪后，描述符向量按照* IJCV *，60（2）：91-110，2004中所述进行重新规范化。

• gamma_correction – bool
  用于指定是否需要伽马校正预处理的标志。 执行伽玛校正会稍微提高HOG算法的性能。

• nlevels – int
  最大检测窗口数增加量。

我们可以看到，cv2.HOGDescriptor()函数支持各种参数。 前几个参数(block_size, block_stride, cell_size, 和 nbins) 可能是最常用的参数。其他参数一般可以保留其默认值，即可获得良好的结果。

在下面的代码中，我们将使用cv2.HOGDescriptor()函数来设置单元格大小，块大小，块步幅以及HOG描述符直方图的 bin 数。 然后使用.compute(image)方法计算给定image的 HOG 描述符（特征向量）。

# 为HOG描述符指定参数

# 像素大小（以像素为单位）（宽度，高度）。 它必须小于检测窗口的大小，
# 并且必须进行选择，以使生成的块大小小于检测窗口的大小。
cell_size = (6, 6)

# 每个方向（x，y）上每个块的单元数。 必须选择为使结果
# 块大小小于检测窗口
num_cells_per_block = (2, 2)

# 块大小（以像素为单位）（宽度，高度）。必须是“单元格大小”的整数倍。
# 块大小必须小于检测窗口。
block_size = (num_cells_per_block[0] * cell_size[0],
              num_cells_per_block[1] * cell_size[1])

# 计算在x和y方向上适合我们图像的像素数
x_cells = gray_image.shape[1] // cell_size[0]
y_cells = gray_image.shape[0] // cell_size[1]

# 块之间的水平距离，以像元大小为单位。 必须为整数，并且必须
# 将其设置为（x_cells-num_cells_per_block [0]）/ h_stride =整数。
h_stride = 1

# 块之间的垂直距离，以像元大小为单位。 必须为整数，并且必须
# 将其设置为 (y_cells - num_cells_per_block[1]) / v_stride = integer.
v_stride = 1

# 块跨距（以像素为单位）（水平，垂直）。 必须是像素大小的整数倍。
block_stride = (cell_size[0] * h_stride, cell_size[1] * v_stride)

# 梯度定向箱的数量
num_bins = 9        


# 指定检测窗口（感兴趣区域）的大小，以像素（宽度，高度）为单位。 
# 它必须是“单元格大小”的整数倍，并且必须覆盖整个图像。 
# 由于检测窗口必须是像元大小的整数倍，具体取决于您像元的大小，
# 因此生成的检测窗可能会比图像小一些。 
# 完全可行
win_size = (x_cells * cell_size[0] , y_cells * cell_size[1])

# 输出灰度图像的形状以供参考
print('\nThe gray scale image has shape: ', gray_image.shape)
print()

# 输出HOG描述符的参数
print('HOG Descriptor Parameters:\n')
print('Window Size:', win_size)
print('Cell Size:', cell_size)
print('Block Size:', block_size)
print('Block Stride:', block_stride)
print('Number of Bins:', num_bins)
print()

# 使用上面定义的变量设置HOG描述符的参数
hog = cv2.HOGDescriptor(win_size, block_size, block_stride, cell_size, num_bins)

# 计算灰度图像的HOG描述符
hog_descriptor = hog.compute(gray_image)

The gray scale image has shape:  (250, 250)

HOG Descriptor Parameters:

Window Size: (246, 246)
Cell Size: (6, 6)
Block Size: (12, 12)
Block Stride: (6, 6)
Number of Bins: 9

4 HOG 描述符中的元素数量

HOG 描述符（特征向量）是由检测窗口中的所有块的所有单元的归一化直方图 concat 起来的长向量。 因此，HOG特征向量的大小将由检测窗口中的块总数乘以每个块的单元数乘以定向箱（bin）的数量来给出：

\begin{equation} \mbox{total_elements} = (\mbox{total_number_of_blocks})\mbox{ } \times \mbox{ } (\mbox{number_cells_per_block})\mbox{ } \times \mbox{ } (\mbox{number_of_bins}) \end{equation}

如果我们没有重叠块（即block_stride等于block_size的情况），则可以通过将检测窗口的大小除以块大小来容易地计算块的总数。 但是，在一般情况下，我们必须考虑到有重叠块的事实。 要查找一般情况下的块总数（即对于任何block_stride 和 block_size），我们可以使用下面给出的公式：

\begin{equation} \mbox{Total}_i = \left( \frac{\mbox{block_size}_i}{\mbox{block_stride}_i} \right)\left( \frac{\mbox{window_size}_i}{\mbox{block_size}_i} \right) - \left [\left( \frac{\mbox{block_size}_i}{\mbox{block_stride}_i} \right) - 1 \right]; \mbox{ for } i = x,y \end{equation}

其中 Total${}_x$，是沿检测窗口宽度的总块数， Total${}_y$， 是沿检测窗口高度的块总数。 Total${}_x$ 和 Total${}_y$的公式考虑了重叠产生的额外块。 在计算 Total${}_x$ 和 Total${}_y$之后，我们可以通过乘法得到检测窗口中的块总数Total${}_x$ $\times$ Total${}_y$。 上面的公式可以大大简化，因为block_size, block_stride,和 window_size都是根据cell_size定义的。 通过进行所有适当的替换和取消，上述公式简化为：

\begin{equation} \mbox{Total}_i = \left(\frac{\mbox{cells}_i - \mbox{num_cells_per_block}_i}{N_i}\right) + 1\mbox{ }; \mbox{ for } i = x,y \end{equation}

其中 cells${}_x$ 是沿检测窗口宽度的单元格总数，cells${}_y$是沿检测窗口高度的单元总数。$N_x$ 是以cell_size 为单位的水平块步幅， $N_y$ 是以 cell_size为单位的垂直块步幅。

下面让我们计算 HOG 特征向量的元素数量，并检查它是否与上面计算的 HOG 描述符的形状相匹配

# 计算沿着检测窗口宽度的总块数
tot_bx = np.uint32(((x_cells - num_cells_per_block[0]) / h_stride) + 1)

# 计算沿着检测窗口高度的块总数
tot_by = np.uint32(((y_cells - num_cells_per_block[1]) / v_stride) + 1)

# 计算特征向量中的元素总数
tot_els = (tot_bx) * (tot_by) * num_cells_per_block[0] * num_cells_per_block[1] * num_bins

# 输出HOG特征向量应具有的元素总数
print('\nThe total number of elements in the HOG Feature Vector should be: ',
      tot_bx, 'x',
      tot_by, 'x',
      num_cells_per_block[0], 'x',
      num_cells_per_block[1], 'x',
      num_bins, '=',
      tot_els)

# 打印HOG描述符的形状，看它是否与上面的匹配
print('\nThe HOG Descriptor has shape:', hog_descriptor.shape)
print()

The total number of elements in the HOG Feature Vector should be:  40 x 40 x 2 x 2 x 9 = 57600

The HOG Descriptor has shape: (57600, 1)

5 可视化 HOG 描述符

OpenCV没有简单的方法来可视化HOG描述符，因此我们必须首先进行一些操作才能使其可视化。我们将从重塑HOG描述符开始，以使我们的计算更加容易。然后，我们将计算每个单元格的平均直方图，最后将直方图bin转换为矢量。一旦有了向量，就可以为图像中的每个单元绘制相应的向量。

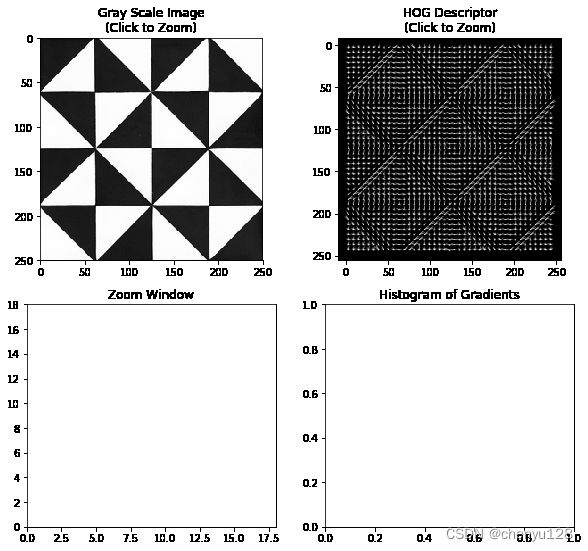
下面的代码生成一个交互式绘图，因此您可以与该图进行交互。该图包含：

• 灰度图像，
• HOG描述符（功能向量），
• HOG描述符的放大部分，以及
• 所选单元格的直方图。

您可以在灰度图像或HOG描述符图像上的任意位置单击以选择特定的单元格。单击任一图像后，将出现一个洋红色矩形，显示您选择的单元格。缩放窗口将为您显示所选单元格周围HOG描述符的放大版本；直方图将为您显示所选单元格的相应直方图。交互式窗口的底部还有一些按钮，允许使用其他功能（例如平移），并且可以根据需要选择保存图形。主页按钮会将图形恢复为其默认值。

注意：如果在Udacity工作区中运行此笔记本，则在交互式绘图中大约有2秒的延迟。这意味着，如果单击图像进行放大，则刷新图大约需要2秒钟。

%matplotlib notebook
%matplotlib inline
import copy
import matplotlib.patches as patches

# 设置默认图形尺寸
plt.rcParams['figure.figsize'] = [9.8, 9]

# 将特征向量重塑为 [blocks_y, blocks_x, num_cells_per_block_x, num_cells_per_block_y, num_bins].
# blocks_x和blocks_y将被换位，以便第一个索引（blocks_y）引用行号
# 第二个索引引用列号。 稍后在绘制特征向量时这将很有用,
# 以便特征向量索引与图像索引匹配。
hog_descriptor_reshaped = hog_descriptor.reshape(tot_bx,
                                                 tot_by,
                                                 num_cells_per_block[0],
                                                 num_cells_per_block[1],
                                                 num_bins).transpose((1, 0, 2, 3, 4))

# 输出特征向量的形状以供参考
print('The feature vector has shape:', hog_descriptor.shape)

# 输出重塑的特征向量
print('The reshaped feature vector has shape:', hog_descriptor_reshaped.shape)

# 创建一个数组，该数组将保存每个单元的平均梯度
ave_grad = np.zeros((y_cells, x_cells, num_bins))

# 输出ave_grad数组的形状以供参考
print('The average gradient array has shape: ', ave_grad.shape) 

# 创建一个数组，该数组将计算每个单元格的直方图数量
hist_counter = np.zeros((y_cells, x_cells, 1))

# 将每个单元格的所有直方图相加并计算每个单元格的直方图数
for i in range (num_cells_per_block[0]):
    for j in range(num_cells_per_block[1]):
        ave_grad[i:tot_by + i,
                 j:tot_bx + j] += hog_descriptor_reshaped[:, :, i, j, :]
        
        hist_counter[i:tot_by + i,
                     j:tot_bx + j] += 1

# 计算每个单元的平均梯度
ave_grad /= hist_counter
   
# 计算在所有单元格中拥有的向量总数。
len_vecs = ave_grad.shape[0] * ave_grad.shape[1] * ave_grad.shape[2]

# 创建一个数组，该数组的num_bins的弧度在0至180度之间。
deg = np.linspace(0, np.pi, num_bins, endpoint = False)

# 每个单元格都有一个带有num_bins的直方图。 对于每个像元，将每个仓绘制为矢量
# （其大小等于直方图中仓的高度，其角度与直方图中的仓对应）。 
# 为此，创建第1级数组，该数组将保留图像中所有单元格中所有向量的（x，y）坐标。
# 此外，创建等级1数组，该数组将保存图像中所有单元格中所有向量的所有（U，V）分量。
# 创建将包含所有向量位置和成分的数组。
U = np.zeros((len_vecs))
V = np.zeros((len_vecs))
X = np.zeros((len_vecs))
Y = np.zeros((len_vecs))

# 将计数器设置为零
counter = 0

# 使用余弦和正弦函数从其大小计算矢量分量（U，V）。 
# 请记住，余弦和正弦函数采用弧度表示角度。
# 从平均梯度数组计算矢量位置和大小
for i in range(ave_grad.shape[0]):
    for j in range(ave_grad.shape[1]):
        for k in range(ave_grad.shape[2]):
            U[counter] = ave_grad[i,j,k] * np.cos(deg[k])
            V[counter] = ave_grad[i,j,k] * np.sin(deg[k])
        
            X[counter] = (cell_size[0] / 2) + (cell_size[0] * i)
            Y[counter] = (cell_size[1] / 2) + (cell_size[1] * j)
        
            counter = counter + 1

# 创建以度为单位的箱，以绘制直方图。
angle_axis = np.linspace(0, 180, num_bins, endpoint = False)
angle_axis += ((angle_axis[1] - angle_axis[0]) / 2)

# 创建一个以2 x 2排列的4个子图的图形
fig, ((a,b),(c,d)) = plt.subplots(2,2)

# 设置每个子图的标题
a.set(title = 'Gray Scale Image\n(Click to Zoom)')
b.set(title = 'HOG Descriptor\n(Click to Zoom)')
c.set(title = 'Zoom Window', xlim = (0, 18), ylim = (0, 18), autoscale_on = False)
d.set(title = 'Histogram of Gradients')

# 绘制灰度图像
a.imshow(gray_image, cmap = 'gray')
a.set_aspect(aspect = 1)

# 绘制特征向量（HOG描述符）
b.quiver(Y, X, U, V, color = 'white', headwidth = 0, headlength = 0, scale_units = 'inches', scale = 5)
b.invert_yaxis()
b.set_aspect(aspect = 1)
b.set_facecolor('black')

# 定义交互式缩放函数
def onpress(event):
    
    #除非按下鼠标左键，否则什么都不做
    if event.button != 1:
        return
    
    # 仅接受子图a和b的点击
    if event.inaxes in [a, b]:
        
        # 获取鼠标点击坐标
        x, y = event.xdata, event.ydata
        
        # 选择最接近鼠标单击坐标的单元格
        cell_num_x = np.uint32(x / cell_size[0])
        cell_num_y = np.uint32(y / cell_size[1])
        
        # 设置矩形面片的边缘坐标
        edgex = x - (x % cell_size[0])
        edgey = y - (y % cell_size[1])
        
        # 创建一个与上面所选单元格匹配的矩形补丁
        rect = patches.Rectangle((edgex, edgey),
                                  cell_size[0], cell_size[1],
                                  linewidth = 1,
                                  edgecolor = 'magenta',
                                  facecolor='none')
        
        # 单个补丁只能在单个图中使用。
        # 创建补丁副本以在其他子图中使用
        rect2 = copy.copy(rect)
        rect3 = copy.copy(rect)
        
        # 更新所有子图
        a.clear()
        a.set(title = 'Gray Scale Image\n(Click to Zoom)')
        a.imshow(gray_image, cmap = 'gray')
        a.set_aspect(aspect = 1)
        a.add_patch(rect)

        b.clear()
        b.set(title = 'HOG Descriptor\n(Click to Zoom)')
        b.quiver(Y, X, U, V, color = 'white', headwidth = 0, headlength = 0, scale_units = 'inches', scale = 5)
        b.invert_yaxis()
        b.set_aspect(aspect = 1)
        b.set_facecolor('black')
        b.add_patch(rect2)

        c.clear()
        c.set(title = 'Zoom Window')
        c.quiver(Y, X, U, V, color = 'white', headwidth = 0, headlength = 0, scale_units = 'inches', scale = 1)
        c.set_xlim(edgex - cell_size[0], edgex + (2 * cell_size[0]))
        c.set_ylim(edgey - cell_size[1], edgey + (2 * cell_size[1]))
        c.invert_yaxis()
        c.set_aspect(aspect = 1)
        c.set_facecolor('black')
        c.add_patch(rect3)

        d.clear()
        d.set(title = 'Histogram of Gradients')
        d.grid()
        d.set_xlim(0, 180)
        d.set_xticks(angle_axis)
        d.set_xlabel('Angle')
        d.bar(angle_axis,
              ave_grad[cell_num_y, cell_num_x, :],
              180 // num_bins,
              align = 'center',
              alpha = 0.5,
              linewidth = 1.2,
              edgecolor = 'k')

        fig.canvas.draw()

# 在图形和鼠标单击之间创建连接
fig.canvas.mpl_connect('button_press_event', onpress)
plt.show()

The feature vector has shape: (57600, 1)
The reshaped feature vector has shape: (40, 40, 2, 2, 9)
The average gradient array has shape:  (41, 41, 9)

6 理解直方图

下面分析一下上图的几个静态截图，看看所选单元格的直方图是否有意义。 让我们开始查看三角形内部而不是边缘附近的单元格：

Fig. 4. - Histograms Inside a Triangle.

在这种情况下，由于三角形几乎都是相同的颜色，因此在所选单元格中不应存在任何主要梯度。 正如我们在缩放窗口和直方图中可以清楚地看到的那样，情况确实如此。 我们有很多渐变但没有一个明显地支配着另一个。

现在让我们看一下靠近水平边缘的单元格：

Fig. 5. - Histograms Near a Horizontal Edge.

请记住，边缘是图像中强度突然变化的区域。 在这些情况下某个特定方向上具有高强度的梯度。 这正是我们在所选单元格的相应直方图和缩放窗口中看到的内容。 在缩放窗口中可以看到主导梯度向上，几乎在90度，因为这是强度急剧变化的方向。 因此，我们应该期望直方图中的90度区域比其他区域更强。 这实际上就是我们所看到的。

现在让我们看一下靠近垂直边缘的单元格：

Fig. 6. - Histograms Near a Vertical Edge.

在这种情况下，我们期望单元中的主导梯度是水平的，接近 180 度，因为这是强度急剧变化的方向。 因此，我们应该期望直方图中的 170 度区域比其他区域梯度影响更大。 这就是我们在直方图中看到的，但我们也看到单元中还有另一个主导梯度，即 10 度 bin 中的梯度。 这是因为 HOG 算法使用无符号梯度，这意味着 0 度和 180 度被认为是相同的。 因此，当创建直方图时，160 度和 180 度之间的角度与 10 度箱（bin）和 170 度箱（bin）成比例。 这导致在垂直边缘附近的单元中存在两个主要梯度而不是仅一个。

总结一下，让我们看一下靠近对角线边缘的单元格。

Fig. 7. - Histograms Near a Diagonal Edge.

为了理解我们所看到的，让我们首先记住梯度由 x 部分（分量）和 y 部分（分量）组成，就像向量一样。因此，梯度的最终方向将由其分量的向量和给出。因此，在垂直边缘上，渐变是水平的，因为它们只有 x 分量，如上图所示。在水平边缘上，渐变是垂直的，因为它们只有 y 分量，正如上上图所示。因此，在对角线边缘，梯度也将是对角线，因为 * x * 和 * y * 分量都是非零的。由于图像中的对角线边缘接近 45 度，我们应该期望在 50 度箱（bin）中看到显著的梯度方向。而这实际上就是我们在直方图中看到的，但是，如上图所示，我们看到有两个主导梯度而不是一个。其原因在于，当创建直方图时，靠近区间边界的角度与相邻区间成比例地起作用。例如，角度为 40 度的梯度位于 30 度和 50 度箱的中间。因此，梯度的大小均匀地分成30度和50度的箱。这导致在对角线边缘附近的单元中存在两个主要梯度而不是仅一个。

现在你知道如何实现HOG，在工作区中将找到一个名为Examples的笔记本。 在这里，你可以为各种图像的HOG描述符设置自己的参数。 玩得开心！