【数据结构】虽然很难很抽象,但是你还是得努力弄懂的数据结构——链表,基本上你每一段代码都可能会用到
链表解决了顺序表插入或删除元素麻烦的问题,链表的存储结构是用一组任意的存储单元来存放线性表的数据元素,这组存储单元可以是连续的,也可以是不连续的。
对每个数据元素ai,除了存储其本身的信息之外,还需存储一个指示其直接后继存放位置的指针。这两部分信息组成数据元素ai的存储映像,称为结点(Node)。如下图所示:
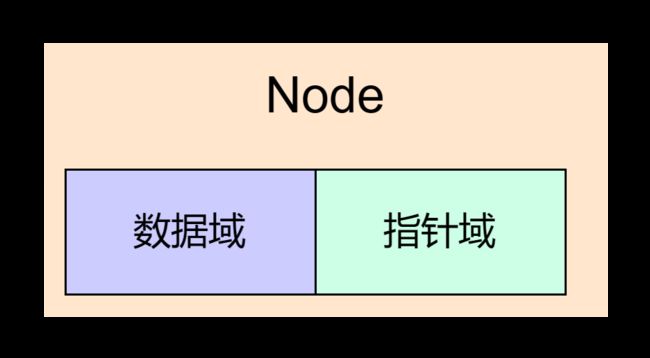
结点类的泛型定义如下,数据域为data,指针域为next。构造器有两个,二者的区别是参数个数不同。有一个参数的构造器,用参数n来初始化next指针域,数据域不存储有效的用户数据。有两个参数的构造器,根据形参obj和n分别初始化数据域data和指针域next。
public class Node<T> {
//数据
T data;
//指针
Node<T> next;
public Node(Node<T> next) {
this.next = next;
}
public Node(T data, Node<T> next) {
this.data = data;
this.next = next;
}
}
public class SingLinkList<T> {
// 头指针
private Node<T> head;
//单链表的长度
private int length;
/**
* 单链表初始化
*/
public SingLinkList() {
length=0;
head = new Node<T>(null);
}
...
}
在SingLinkList类中有两个成员变量。一个是指向头结点的指针head,习惯称head为头指针;另一个是length,用来存放单链表的长度。类中的基本方法和顺序表中的基本方法实现的功能是一样的,但具体实现有所区别。
在无参构造方法中,设置length值为0即初始化线性表为空。通过new创建的结点对象调用了Node(Node
单链表的插入是指在单链表的第pos-1个结点和第pos个结点之间插入一个新的结点,要实现结点的插入,需修改插入位置之前的结点和当前插入结点的指针指向,过程如下图:

具体实现代码如下:
/**
* 单链表的插入,需要把插入位置的上一个节点和下一个节点先找出来,然后插入 时间复杂度为O(n)
* @param obj 需要插入的元素
* @param pos 需要插入的位置
* @return
*/
public boolean add(T obj,int pos){
if (pos < 1 || pos > length+1) {
throw new LinkException("pos值不合法");
}
int num =1;
// 当前节点, 需要从头开始查找
Node<T> p = head;
// 下一个结点
Node<T> q = head.next;
// 从头结点开始一个个找到需要删除的结点
while (num<pos){
// 保留下一个结点
p =q;
//获取下一个结点
q=q.next;
num++;
}
// 插入一个新节点
p.next=new Node<>(obj,q);
length ++;
return true;
}
从代码可知,链表的插入操作首先需要检查参数pos的合法性,当1≤pos≤length时,初始化num为1,变量引用单链表中头结点之后的第一个结点,之后q每后移一个位置q=q.next,num就加1,循环num-1次后,就可以找到第pos个结点。要删除的第pos个结点,通过q引用,被删除结点的前一个结点,通过变量p引用。要把元素x插入到链表中,首先应该构建一个Node对象,数据域data的值为x,定义Node
由于链表不具有随机访问的特点,所以插入操作之前,要从单链表的头结点开始,顺序扫描每个结点并计数,从而找到插入位置,即第pos个结点,时间主要用来查找插入位置,该算法的时间复杂度为O(n)。
单链表的删除是指删除单链表的第pos个结点,要实现该结点的删除,可将删除位置之前的结点,即第pos-1个结点的指针域指向第pos+1个结点。删除过程如下;
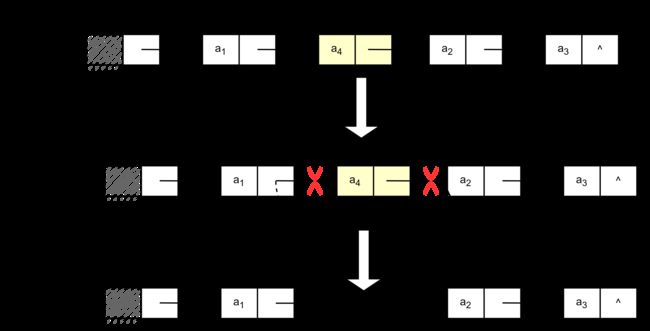
单链表进行插入操作的前提是链表不为空,条件满足之后,分别找到要删除的pos个结点,通过q引用,和被删除结点的前一个结点(通过变量p引用),修改p引用结点指针域的值即可完成删除操作,语句为p.next=q.next,删除操作完成后,链表长度减1,并返回被删除结点数据域的值。删除代码如下:
/**
* 单链表的删除某个结点,需要把插入位置的上一个节点和下一个节点先找出来,然后删除 时间复杂度为O(n)
* @param pos 需要删除的结点
* @return
*/
public T remove(int pos){
if (isEmpty()){
throw new LinkException("链表为空");
}else {
if (pos < 1 || pos > length) {
throw new LinkException("pos值不合法");
}
int num =1;
// 当前节点, 需要从头开始查找
Node<T> p = head;
// 下一个结点
Node<T> q = head.next;
// 从头结点开始一个个找到需要删除的结点
while (num<pos){
// 保留下一个结点
p =q;
//获取下一个结点
q=q.next;
num++;
}
// 把q节点删除
p.next =q.next;
// 链表长度减少1
length--;
return q.data;
}
}
单链表的查找思路和顺序表类似,值得注意的是:由于构建的是带有头结点的单链表,所以首先变量p引用的是头结点之后的结点,当该结点不存在时链表即为空。通过调用方法equals来判断两个对象的值是否相等,查找成功返回对象obj在单链表中的位序,查找失败返回-1,代码实现如下:
/**
* 单链表的查找 时间复杂度为O(n)
* @param obj 需要查找的值
* @return num 需要查找的值对应的节点位置. -1 表示未找到,
*/
public int find(T obj){
if (isEmpty()){
throw new LinkException("链表为空");
}
int num=1;
// p引用的是头结点之后的节点
Node<T> p=head.next;
//如果单链表不为空
while (p!=null){
//如当前节点的data不等需要查找的值,就继续查找下一个节点
if (!p.data.equals(obj)){
p = p.next;
num++;
}else {
break;
}
}
if (p == null){
return -1;
}
return num;
}
单链表的完整实现如下:
public class SingLinkList<T> {
// 头指针
private Node<T> head;
//单链表的长度
private int length;
/**
* 单链表初始化
*/
public SingLinkList() {
length=0;
head = new Node<T>(null);
}
/**
* 获取单链表头结点的地址
* @return
*/
public Node<T> getHead(){
return head;
}
/**
* 单链表的插入,需要把插入位置的上一个节点和下一个节点先找出来,然后插入 时间复杂度为O(n)
* @param obj 需要插入的元素
* @param pos 需要插入的位置
* @return
*/
public boolean add(T obj,int pos){
if (pos < 1 || pos > length+1) {
throw new LinkException("pos值不合法");
}
int num =1;
// 当前节点, 需要从头开始查找
Node<T> p = head;
// 下一个结点
Node<T> q = head.next;
// 从头结点开始一个个找到需要删除的结点
while (num<pos){
// 保留下一个结点
p =q;
//获取下一个结点
q=q.next;
num++;
}
// 插入一个新节点
p.next=new Node<>(obj,q);
length ++;
return true;
}
/**
* 单链表的删除某个结点,需要把插入位置的上一个节点和下一个节点先找出来,然后删除 时间复杂度为O(n)
* @param pos 需要删除的结点
* @return
*/
public T remove(int pos){
if (isEmpty()){
throw new LinkException("链表为空");
}else {
if (pos < 1 || pos > length) {
throw new LinkException("pos值不合法");
}
int num =1;
// 当前节点, 需要从头开始查找
Node<T> p = head;
// 下一个结点
Node<T> q = head.next;
// 从头结点开始一个个找到需要删除的结点
while (num<pos){
// 保留下一个结点
p =q;
//获取下一个结点
q=q.next;
num++;
}
// 把q节点删除
p.next =q.next;
// 链表长度减少1
length--;
return q.data;
}
}
/**
* 单链表的查找 时间复杂度为O(n)
* @param obj 需要查找的值
* @return num 需要查找的值对应的节点位置. -1 表示未找到,
*/
public int find(T obj){
if (isEmpty()){
throw new LinkException("链表为空");
}
int num=1;
// p引用的是头结点之后的节点
Node<T> p=head.next;
//如果单链表不为空
while (p!=null){
//如当前节点的data不等需要查找的值,就继续查找下一个节点
if (!p.data.equals(obj)){
p = p.next;
num++;
}else {
break;
}
}
if (p == null){
return -1;
}
return num;
}
/**
* 获取单链表第pos个结点的值, 从头节点开始往下查找, 时间复杂度为O(n)
* @param pos 需要查找的结点位置
* @return 需要查找的结点位置对应的值data
*/
public T value(int pos){
if (isEmpty()){
throw new LinkException("链表为空");
}else{
if (pos<1 || pos>length){
throw new LinkException("pos值不合法");
}
//当前节点的位置
int num =1;
Node<T> q =head.next;
while (num<pos){
q= q.next;
num++;
}
return q.data;
}
}
/**
* 更新单链表第pos个结点的值 ,时间复杂度为O(N) ,需要从头节点开始查找
* @param obj 需要更新的值
* @param pos 需要更新的结点的位置
* @return
*/
public boolean modify(T obj,int pos){
if (isEmpty()){
throw new LinkException("链表为空");
}else {
if (pos < 1 || pos > length) {
throw new LinkException("pos值不合法");
}
//当前节点的位置
int num =1;
Node<T> q =head.next;
while (num<pos){
q= q.next;
num++;
}
q.data=obj;
return true;
}
}
/**
* 获取单链表的长度
* @return 单链表的长度
*/
public int size(){
return length;
}
/**
* 清空单链表
*/
public void clear(){
length=0;
head.next= null;
}
/**
* 打印节点的元素
*/
public void show(){
System.out.println("");
System.out.print("打印节点元素:");
//获取头节点的下一个节点
Node<T> p= head.next;
while (p!=null){
System.out.print(p.data+"-->");
//获取下一个节点
p =p.next;
}
}
/**
* 判断单链表是否为空
* @return
*/
public boolean isEmpty(){
return length==0;
}
public static void main(String[] args) {
SingLinkList<Integer> singLinkList = new SingLinkList<>();
int l,i;
int[] a ={10,12,3,8,6,4,9};
l=a.length;
for (i=0;i<l;i++){
singLinkList.add(a[i],i+1);
}
singLinkList.size();
singLinkList.show();
singLinkList.remove(4);
singLinkList.size();
singLinkList.show();
}
}
循环链表是另一种形式的链表,它的特点是表中最后一个结点的指针域不再为空,而是指向表头结点,整个链表形成一个环。
双向链表也是一种形式的链表,相比单链表多了一个指向前驱的指针,找其前驱节点的时间复杂度从O(n)提升到O(1)。双向链表的结点结构如下图所示:

结点描述代码如下:
public class Node<T> {
//数据
T data;
//前指针
Node<T> prior;
//后指针
Node<T> next;
public Node(T data) {
this.data = data;
prior=null;
// next=null;
}
public Node(T data, Node<T> prior, Node<T> next) {
this.data = data;
this.prior = prior;
this.next = next;
}
}
和单链表类似,双向链表也可以有循环表,循环双向链表图示如下:
由于循环单链表、双向链表、循环双向链表不是本文的重点,具体不在赘述。有兴趣的的小伙伴可自行阅读相关数据结构与算法的书籍。


