基于tushare和python的证券市场价格分析

基于tushare和python的证券市场价格分析

证券资产的定价及其价格运动规律的描述长期以来都是一大难题，本文中我们运用相关金融计量和计算机基础知识原理对这一运动规律进行初步拟合和探究。

---

---

前言

本文通过结合运用tushare和python两大技术手段，对沪深两地股票运动规律的描述进行了实证分析和研究。我们在证券市场中筛选出10只具有较好代表性的股票，通过tushare接口导入各股票的日线数据，调用python中相关包绘制出相应的统计直方图，验证了股票收益率符合正态分布，进而验证了股票走势较好符合布朗运动规律、维纳过程和伊藤过程的这一基础理论事实。

提示：以下是本篇文章正文内容，下面案例仅供参考

一、相关理论公式

二、tushare与python的运用

tushare平台是一个免费、开源的python财经数据接口包，能够实现对股票等金融数据从数据采集、清洗加工到数据存储的过程，使金融分析人员更加专注于策略和模型的研究与实现上。Tushare返回的绝大部分数据都是pandas.DataFrame格式，便于在python中采用pandas/NumPy/Matplotlib等工具进行金融量化分析和数据可视化。 在本次研究分析过程中，我们首先根据股票大致分类结果，从股票市场上选取中国平安（601318）、中国银行（601988）、建设银行（601939）、贵州茅台（600519）、科大讯飞（002230）、五粮液（000858）、比亚迪（002594）、太平洋（601099）、宝钢股份（600019）、招商银行（600036）这十只股票进行研究。

import tushare as ts
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import config
import math

ts.set_token(config.token)
#本代码用于从tushare上获取10只具有典型代表性的股票日线数据

#获取正态分布曲线
def normfun(x, mu, sigma):
    pdf = np.exp(-((x - mu) ** 2) / (2 * sigma ** 2)) / (sigma * np.sqrt(2 * np.pi))
    return pdf
def predicte(s,u,r,dt):
    return math.exp(math.log(s)+(u-0.5*r**2)*dt)
#将股票代码存至列表，按列表中元素进行依次处理
stock=['601318','601988','601939','600519','002230','000858','002594','601099','600019','600036']

此后，我们通过python调用tushare的pro_bar接口，获取自2016年1月1日到2021年6月4日共计1318个交易日的日线数据，分别取得各交易日的开盘价（open）、最高价（high）、最低价（low）、收盘价（close）、昨收价（pre_close）、涨跌额（change）、涨跌幅（pct_chg）、成交量（vol）、成交额（amount）信息。

for i in stock:
    if int(i)>600000:#区分上证和深证指数
        tscode=str(i)+'.SH'
    else:
        tscode=str(i)+'.SZ'
    df = ts.pro_bar(ts_code=tscode, adj='qfq', start_date='20160101', end_date='20210604')#读取该时间区间的股票数据
    df = df.sort_values(by="trade_date",ascending=True)#按时间升序对原始数据进行排序
    filepath="D:/Documents/finance/"+str(i)
    df.to_csv(filepath+'.csv')#转为.csv表格，便于读取分析

将数据按交易日期升序排序后，通过.to_csv函数保存至csv表格中，并利用pandas工具读入并整理对应项的数据。此后，对数据进行量纲调整、归一化处理，并将其划分至bins或类别中。采用matplotlib包提供的绘图指令，将上述10只股票在1318个交易日内的收益率（pct_chg）按频率统计直方图的形式进行绘制，并根据数据中收益率的均值及方差在图上加入正态曲线拟合。

 	ds = pd.read_csv(filepath+".csv",index_col="ts_code")[["pct_chg","close"]]#按特定项读入数据
    mean=ds['pct_chg'].mean()#求取收益率的平均值
    std=ds['pct_chg'].std()#求取收益率的方差
    maxd=int(max(-ds['pct_chg'].min(),ds['pct_chg'].max()))#求取收益率的极值的绝对值
    x = np.arange(-maxd-2, maxd+2,maxd/30)#设定绘图自变量区间，使可视化效果更佳
    y = normfun(x, mean, std)*len(ds)#拟合正态曲线，同时逆均一化
    plt.plot(x, y)#绘制正态曲线图
    n, bins, patches = plt.hist(ds['pct_chg'], bins=int(13+maxd), facecolor='green', alpha=0.75)#绘制频率直方图
    plt.xlabel('pct_chg')
    plt.title('Stock:'+i+'\'s distribution map')
    plt.text(-maxd-2,n.max(),"mean="+str(mean),fontsize=8)
    plt.text(-maxd-2,int(n.max()*29/30),"std="+str(std),fontsize=8)
    plt.text(-maxd-2,int(n.max()*28/30),"max="+str(ds['pct_chg'].max()),fontsize=8)
    plt.text(-maxd-2,int(n.max()*27/30),"mix="+str(ds['pct_chg'].min()),fontsize=8)
    plt.savefig(filepath+".png")
    plt.close()

三、实证结果

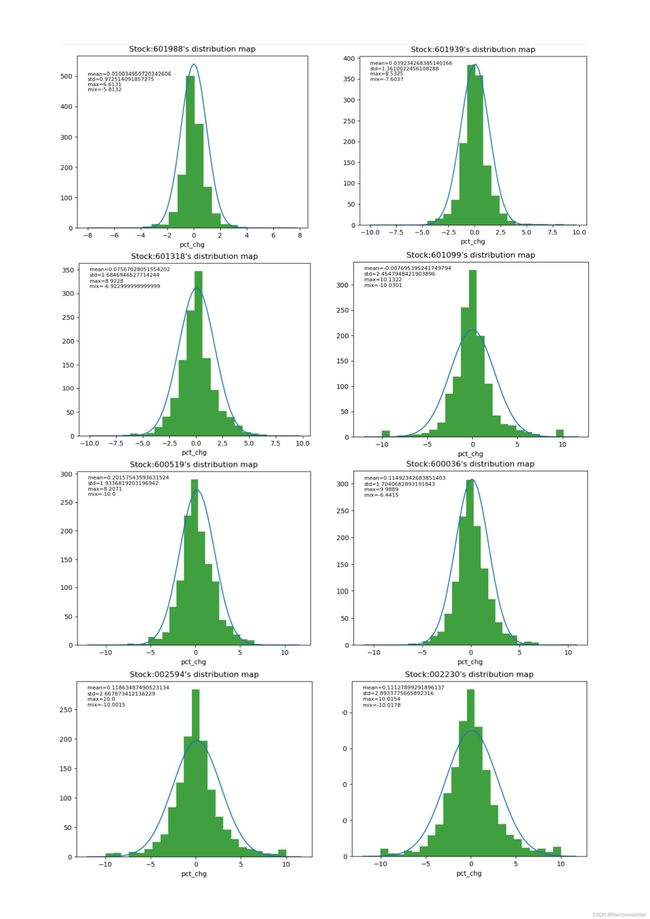
根据上述tushare与python操作，绘制出10只股票收益率的直方图及其对应的正态拟合曲线如下图：

总结

上图可见，10只股票的收益率均能较好地满足正态分布规律，这与金融工程理论课堂上所介绍的标的资产价格的伊藤过程相符合。但仔细观察其直方图可得，其峰度略高于正态分布曲线，表明我国证券市场价格稳定性较优，市场调控机制较为完善。
tushare这一工具的使用也为资本市场证券价格的调研提供了充分便利，能够将资本市场的各类金融数据轻易保存至本地。tushare接口所提供导出的数据格式，也能较好发挥python这一高级编程语言及其配套环境的资源禀赋优势，更好助力金融计量程序员理解和分析相关数据。欢迎各位感兴趣的同仁登录tushare官方网站获取更多信息！