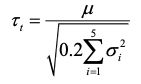机器学习基础知识之多模型性能对比评价方法
文章目录
- 1、交叉验证t检验
- 2、Friedman检验与Nemenyi后续检验
在进行预测或分类对比实验时,通常需要比较两个或两个以上的模型性能,因此,下面将介绍两个常用的多模型性能对比评价方法,一种是交叉验证t检验,该方法主要用于同一个数据集上两个模型的性能比较,另一种是Friedman检验与Nemenyi后续检验,这一方法主要用于同一组数据集上两个以上模型的性能比较。
1、交叉验证t检验
之前介绍过k折交叉验证方法,该方法将同一个数据集随机平均分成k份,然后让每一份依次作为测试数据集,余下数据作为训练数据集,使模型在训练数据集上训练后在测试数据集上进行测试以获得该模型在每份数据集上的误差,最后将误差值进行平均即为模型在此数据集上的最终误差值。而交叉验证t检验则是专门针对两个不同的模型在同一个数据集上进行k折交叉验证后的性能比较方法。
假设对于两个不同的模型A与模型B,在同一个数据集上进行k折交叉验证后得到的每份数据集上的误差分别如下:
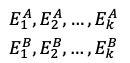
则需要将这两个模型在k份测试数据集上的误差进行一对一的比较,而当这两个模型的性能相同时,则这两个模型在同一份测试数据集上误差应该相同,即:
![]()
i为1到k之间的任意正数。
其具体的比较过程为首先对两个模型在k份测试数据集上的误差进行一对一的比较,求取它们之间的差值,计算公式如下:
![]()
然后对求得的差值∆_1,∆_2,…,∆_k进行均值与方差的计算,计算获得的均值与方差分别为μ和σ^2,在显著度α下,倘若变量
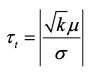
小于临界值t_(α/2,k-1),则可以视作这两个模型的性能没有显著差别。若大于该临界值,则这两个模型的性能存在显著差别,其中平均误差较小的模型的性能更好。上述临界值t_(α/2,k-1)是自由度为k-1的t分布上尾部累积分布为α/2的临界值。
由于是在同一份数据集上进行交叉验证,因此当数据量较少时容易使得不同训练数据集之间容易存在一定程度的重叠,进而导致最后容易认为两个模型性能不存在显著差别。为了避免这一问题,一般采用“5×2交叉验证法”。
5×2交叉验证是指在数据量较少时,对两个模型进行5次2折交叉验证,其中在每次2折交叉验证前将数据集进行随机打乱,从而使5次验证过程中数据集的划分均不重复。
在上述2折交叉验证中分别计算获得两个不同的差值:
![]()
为了使误差结果更具有独立性,将第一次交叉验证中这两个不同的差值的平均值μ作为判断依据,在对方差进行求取时则是对每次交叉验证的差值结果进行计算,计算公式如下:
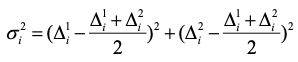
小于临界值t_(α/2,5),即服从自由度为5的t分布时,这两个模型的的性能没有显著差别,否则存在显著差别,其中平均误差较小的模型的性能更好。在此计算公式下,当α取值为0.05时,临界值t_(α/2,5)为2.5706,当α取值为0.1时,临界值t_(α/2,5)为2.015。
2、Friedman检验与Nemenyi后续检验
上述交叉验证t检验是在一个数据集上对两个不同的模型性能进行比较,而当需要在一组数据集上对多个模型的性能进行比较时,则需要使用Friedman检验。Friedman检验是一种基于模型性能排序的检验方法,它在同一个数据集上依据某些性能评价指标对多个模型的性能好坏进行排序,进而获得多个模型在一组数据集上的性能排序结果,依照此结果平均计算得到在这组数据集上的平均性能排序,倘若不同模型的性能相同时,它们的平均性能排序应该相同。
假设使用三个不同的模型A、模型B以及模型C在三个不同数据集D_1、D_2、D_3上进行预测实验,通过使用上一小节中提到的预测性能评价指标均方误差对它们的预测性能进行评价,倘若在数据集D_1上三个模型的均方误差值大小排序依次为模型A、模型B和模型C,那么将对模型A、模型B和模型C分别赋予序值1,2,3。按照此方法,对这三个模型在另外两个数据集上的均方误差值大小进行排序,可获得模型性能排序表如下所示。
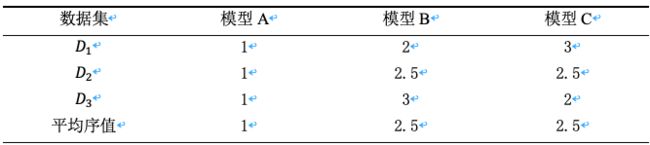
上表中在数据集D_2上,当两个模型的均方误差值相同时,则对它们的序值进行平分,即出现模型B与模型C的序值均为2.5的情况。最后一行则是通过对这三个模型在三个不同数据集上的性能序值求平均而得到平均序值,当不同模型的平均序值相同时,可以视作这两个模型的性能相同。
为了方便判断,直接通过计算变量
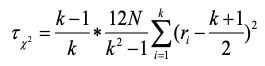
来确定模型的性能是否相同,上式中r_i表示第i个模型性能的平均序值,N为数据集的个数,k为模型的个数,抛开平均序值的考虑时,(k+1)/2为符合正太分布的r_i的均值,方差为(k^2-1)/12N。
当k与N都较大时,该变量服从自由度为k-1的χ^2分布。
上述变量的计算方式较为保守,现在通常使用变量
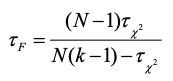
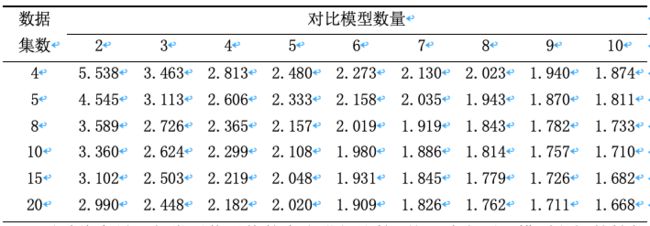
来进行判断,其中τ_F服从自由度为k-1和(k-1)(N-1)的F分布,当计算之后变量τ_F小于临界值时,可以视作这几个对比模型的性能没有显著差别,若大于该临界值,则这几个对比模型的性能显著不同。下面两张表分别是显著度为0.05与0.1时的常用临界值。
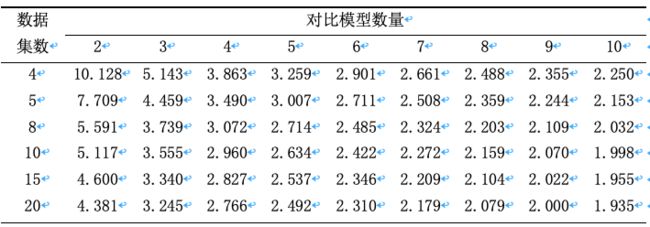
通过将变量τ_F与常用临界值的大小进行比较,从而确定不同模型之间的性能是否显著相同,当确定显著不同时,则需要使用Nemenyi后续检验来对其不同模型的性能做进一步的区分。
在进行Nemenyi后续检验时需要通过下列公式计算得出模型平均序值差别的临界值域,具体的计算公式如下:
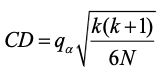
当两个模型的平均序值之差超过了计算得出的临界值域CD,则可以确定两个模型之间存在明显差别。另外对上述结果的比较检验将通过Friedman检验图进行更为清晰的表示,在Friedman检验图中,横轴为平均序值,纵轴表示不同的模型,当代表两个模型的横线之间不存在交叠时,则说明两个模型之间存在显著差别,否则它们之间不存在显著差别,常见的Friedman检验图如下图所示。

在上图中,代表模型1的直线的边缘与代表模型2和模型3的直线明显存在交叠,则说明这三个模型之间不存在显著区别,但从它们的平均序值可以看到模型1的平均序值大于模型2与模型3,因此模型1的性能略优于另外两个模型。另外代表模型1的直线与代表模型4与模型5的之间之间不存在交叠,则说明模型1与另外两个模型之间存在显著区别,且其平均序值最大,即模型1的性能明显优于模型4与模型5。结合上述比较结果可以得知,模型1的性能在这五个模型中表现最好。
在对Friedman检验与Nemenyi后续检验可以得知,此方法主要用于在一组数据集上对多个模型的性能进行比较,而在实际应用过程中,可以将此方法进行扩展,例如在群智能优化算法的性能进行比较时,可以使用此方法比较多种不同的算法在一组测试函数上的性能;当对一个数据集上的多种预测模型性能进行比较时,可以计算得出模型的多种性能指标结果,然后比较多种性能指标上的模型性能情况。