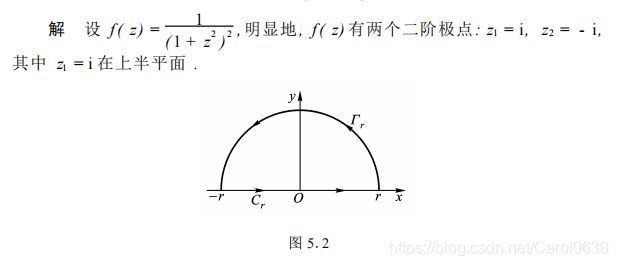
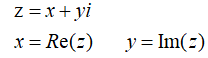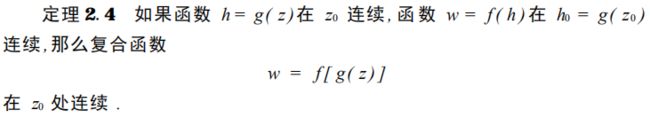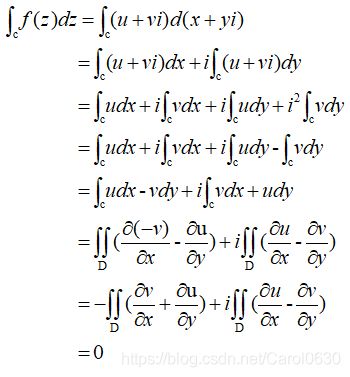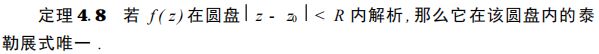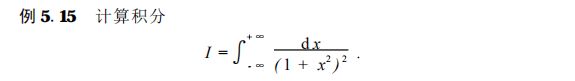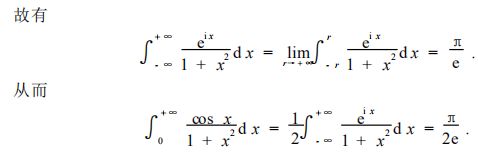【算法】复变函数

前言

• 复变函数是由一个复数域映射到另一个复数域的关系。判断复变函数是否可导可导：u( x , y ) 和 v ( x , y ) 在点 ( x, y ) 可微, 并且在该点 满足柯西—黎曼方程。解析函数是复变函数在一个区域内可导。可用定义法计算复变函数在一点的导数 或 利用常见初等函数的导数以及导数的运算法则求导。
• 柯西定理：已知一复变函数的原函数，可求其积分。柯西定理证明了若一正向封闭区域内（逆时针），若所积函数解析，则其积分为零。
  
• 柯西积分公式：当复变函数在封闭区域内解析，则在该封闭区域内任一点的值由f(z)/z-z₀在边界上的积分所决定。
  
  如果一个函数在某点解析,那么它的各阶导函数在该点仍解析 。设 f ( z)在简单正向闭曲线 C 及其所围区域 D 内处处解析, z₀ 为 D 内任一点, 那么:
  
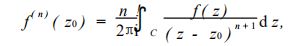
  由此，一般解析初等函数可以展开为对应泰勒级数。且部分函数可展开为含负幂次项的洛朗级数。
  根据展开函数的级数在某一点或无穷远点的负幂次项的个数，可将奇点类型分为：可去奇点、极点、本性奇点。同时，根据留数定理可求出对应展开级数的C_-1项的系数从而求出某封闭曲线上的积分。留数对一些特殊的定积分的计算。

复数

1. 复数的代数运算：

2. 复数四则运算的几何意义：

①两个复数乘积的模等于它们模的乘 积;两个复数乘积的幅角等于它们幅角的和
②两个复数商的模等于它们模的商; 两个复数商的幅角等于被 除数与除数的幅角差
③复数的加减：

3. 复数的幂乘和方根

①幂乘
②方根(这里 w≠0 , n≥2 )的复数 w 为该方程的 n 次方根

复变函数

复数域上初等函数的定义：

1. 指数函数

性质：e^z+2kπ=e^z,故指数函数e^z是一个以2π为周期的周期函数。

故e^z在复平面上处处可导，解析。

2. 对数函数

性质：w 是 z 的对数函数,记为 w = Ln z .其为多值函数。单值函数为多值函数 Ln z的主值,记作 ln z .

3. 幂函数

4. 三角函数与反三角函数

①正弦与余弦函数

由上面的定义,我们可以容易地推出正弦函数和余弦函数的下述性质:(*)
②其他三角函数
③反三角函数

5. 双曲函数与反双曲函数

导数

1. 复变函数极限

①复变函数极限概念：

②复变函数极限判断定理：

2. 复变函数的连续性

①复变函数连续概念：

②复变函数连续性定理：

3. 导数

①定义：（可导必连续，连续不一定可导）

例1 求zⁿ的导数

例2 证明

例3 证明f(z)=|z|²的可导性


②导数的运算法则：


③函数可导的充分必要条件：

4. 解析函数

①定义：（区域内所有点可导）

由定义知,函数在区域 D 内解析与在区域 D 内可导是等价的 .但函数在 一点解析与在该点可导是绝对不等价的 .前者比后者条件强的多, 函数在某点 解析意味着函数在该点及其某邻域内处处可导;而函数在某点可导, 在该点邻 域内函数也可能可导,也可能不可导 .
②判断定理：

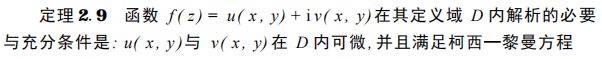
由导数的运算法则可知,在某区域上解析的函数经过加、减、乘、除 (分母 不为零)运算得到的函数在该区域上仍解析 .两个及两个以上的解析函数经过 有限次复合运算后得到的函数仍为解析函数 .解析函数的单值反函数仍为解 析函数

5. 调和函数

积分

1.积分的概念、性质、计算

将实数域上有关积分的概念、性质推广到复数域上
1.原函数：

2.不定积分：

3. 常见公式：

4. 定积分：


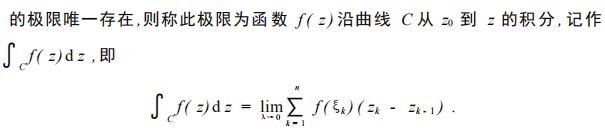
定积分性质：

5.计算：

2. 柯西定理及其推广

3.柯西积分公式

定理：推导前提：

4. 解析函数的导数

级数

1.收敛序列和收敛级数

①收敛序列：

②收敛数项级数：



③函数项级数：

2. 幂级数

定义：

幂级数的收敛半径：
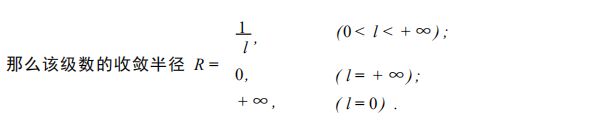
幂级数的和函数的性质：

在高等数学中,我们将一个具有 n + 1 阶导数的函数展为泰勒级数或麦 克劳林级数 .在下一节我们将解析函数 ( 具有任意阶导数 ) 展为泰勒级数或麦 克劳林级数,也就是解析函数展为幂级数 .

3.泰勒级数

例1

4.洛朗级数

有些函数虽然不能表示为泰勒级数, 但是却能用含有负指数幂 的级数在某个圆环内表示,这种含有负指数幂的级数就是下面要讨论的罗朗 级数

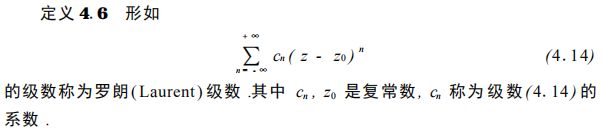
留数

1.解析函数的孤立奇点

1.可去奇点、极点、本性奇点

• 可去奇点、极点、本性奇点
  分别对应罗郎展开式中无负次幂，只有有限个负次幂和无限个负次幂。

2.零点定义





3.解析函数在无穷远点的性质

2.留数的一般理论

1.留数的定义


2.极点处留数的求法（既求拆开的对应c_-1的系数）

3.留数对定积分的计算

在高等数学以及实际问题中,常常需要求出一些定积分或广义积分的值, 而这些积分中被积函数的原函数,不能用初等函数表示出来, 或即使可以求出 原函数,计算也往往比较复杂 .利用留数定理, 要计算某些类型的定积分或广 义积分, 只须计算某些解析函数在孤立奇点的留数, 从而把问题大大简化, 下 面通过具体例子,说明如何利用留数计算几种特殊类型的积分 .

1.含sinx，cosx的有理分式积分


2.

3.

保形映射

解析函数对平面向量场的应用