WorldWind源码剖析系列：四元数类Quaternion

PluginSDK中的Quaternion4d类可能是感觉Microsoft.DirectX. Quaternion类不太实用或不够用，自己有重新写的。

四元数是英国数学家哈密顿(W.R.Hamilton)在1843年发现的，由于矩阵论的不断丰富和不断完善，人们更乐意采用矩阵来解决实际工程中的问题，这导致四元数在相当长的时间里没有被人们重视，更没有得到实际的应用。随着计算机图形学的发展，人们发现利用四元数可以很好地处理解决旋转运算等问题，这一理论又开始被人们重视，并在许多领域逐渐得到应用。

四元数将三维中旋转的概念扩展到四维中的旋转，在DirectX 中提供了Quaternion类用于定义四元数对象和四元数计算，该结构描述一个四维向量（x,y,z,w），通过四元数可将一个对象绕向量(x,y,z)旋转一个角度theta，其中w=cos(theta/2)。四元数运算在这个计算中比用矩阵计算效率更高。对于一个旋转轴Axis （Axis.x, Axis.y, Axis.z）（将轴分量单位化），  theta为要绕轴旋转（以逆时针旋转）的角度，则可以用一个四元数q(x,y,z,w)来表示，其各元素值为：

q.X = sin(theta/2) * Axis.x

q.Y = sin(theta/2) * Axis.y

q.Z = sin(theta/2) * Axis.z

q.W = cos(theta/2)

Quaternion4d类的类图如下所示。

 

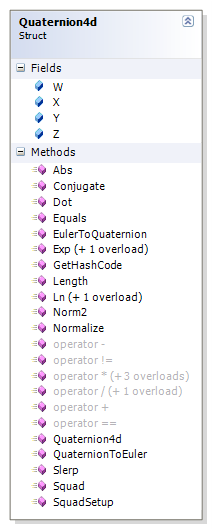
　　静态方法static Quaternion4dEulerToQuaternion(double yaw, double pitch, double roll)用于将航偏角yaw、倾斜角pitch和横滚角roll等欧拉角转换为四元数对象。

　　静态方法static Point3d QuaternionToEuler(Quaternion4d q) 用于将表示旋转的四元数对象转换为航偏角yaw、倾斜角pitch和横滚角roll等欧拉角。

重载了加、减、乘、除、等于、不等于等运算符用于点对象运算。

　　Conjugate、Norm2、Abs、Dot、Normalize、Length、Slerp、Ln、Exp、Squad、Squad、SquadSetup等定义了关于四元数的基本操作。具体含义请查阅相关文献。