2023华中杯数学建模C题完整模型代码

 已完成全部模型代码，文末获取。

摘要

随着工业化和城市化的快速发展，空气污染已经成为全球性的环境问题。细颗粒物（PM2.5）等污染物对人类健康、生态环境和社会经济造成了严重影响。本研究旨在深入探究影响PM2.5浓度的主要因素，并构建一个有效的多步预测模型。为此，我们采用了数据挖掘、机器学习和统计分析等方法，对大量污染物浓度和气象数据进行了综合分析。

首先，本文对附件1和附件2的数据进行了分析和处理，筛选出与PM2.5浓度变化相关的因素，包括PM10、CO、气温、风速和降水量。通过相关性分析和多元线性回归模型，分析了这些因素对PM2.5浓度的影响程度。结果表明，PM10和CO对PM2.5浓度影响最大，气温和风速次之，降水量对PM2.5浓度影响相对较小。

本文将数据集划分为训练集和测试集，基于问题一的结果构建了PM2.5浓度的多步预测模型。为了获得最佳预测效果，分别尝试了多种预测模型，如ARIMA模型、支持向量机（SVM）模型、人工神经网络（ANN）模型和长短时记忆（LSTM）神经网络模型。通过对比各模型在不同预测步长下的均方根误差（RMSE），最终选定了表现最优的模型。使用选定的模型对3步、5步、7步和12步预测效果进行了评估，具体结果如表1所示。对测试集及其预测结果进行了可视化分析，以便更直观地展示预测效果。

本文构建了AQI多步预测模型，并使用均方根误差（RMSE）对建模效果进行评估。同样，通过对比不同模型的预测效果，选定了最佳模型。对测试集及其预测结果进行了可视化分析。利用该模型预测了附件3所给定时间的AQI，并根据预测结果给出了每天空气质量的预警等级。预测结果以及预警等级划分如表3和表4所示。本研究为更精确地预测PM2.5浓度和AQI指数，解析污染影响因素和制定有效控制策略提供了理论依据。

此外，本文还探讨了不同预警等级下的应对措施，以期为地方政府和相关部门提供参考。针对蓝色、黄色、橙色和红色预警等级，分别提出了不同程度的限行、限产、停工、停课等应急措施，以最大程度降低污染天气的影响。此外，还针对不同预警等级提出了节能减排、科学调度和宣传教育等长期治理措施，以期提高重污染天气预防预警、应急响应能力和环境精细化管理水平。

关键词：空气污染；多步预测模型；均方根误差；应急预案

一、问题重述

1.1 问题背景

随着工业化进程的加速和人类活动的不断增加，空气污染已经成为全球性的环境问题。空气污染对人类健康、生态环境、社会经济造成危害，其污染水平受诸多因素的影响，如 PM2.5、PM10、CO、气温、风速、降水量等。PM2.5 是指空气中直径小于等于 2.5 微米的颗粒物，它能够进入人体呼吸道和肺部，对人体健康产生不良影响。AQI 是空气质量指数，是根据空气中的污染物浓度计算出来的一个数值，它直接反映了空气质量的好坏程度。

因此，探究 PM2.5 等污染物浓度的因素，更精准的预测 PM2.5 浓度和 AQI 指数等是科学界和决策者共同关心的问题。为了健全和针对完善重污染天气的应对处置机制，提高重污染天气预防预警、应急响应能力和环境精细化管理水平，消除重度及以上污染天气，作为突发环境事件应急预案体系的重要组成部分，某地发布污染天气应急预案，其预警等级划分为四级应急响应，即蓝色预警、黄色预警、橙色预警和红色预警。预测空气质量和 AQI 的等级，对于解析污染影响因素和有效制订控制策略具有重要意义。

1.2 问题重述

问题一：根据附件1和附件2，对数据进行分析和处理，筛选出与PM2.5浓度变化有关的因素，并说明筛选出的因素对PM2.5 浓度影响的程度。

问题二：自行划分训练集和测试集，根据附件 1 和附件 2，基于问题一构建 PM2.5浓度多步预测模型，分别使用均方根误差（RMSE）对3步、5步、7步、12 步预测效果进行评估，其结果请用表1格式在正文中具体给出，并对测试集及其预测结果进行可视化。

同时，用该模型预测附件3所给定时间的PM2.5浓度，其结果请用表2格式在正文中具体给出。

问题三：构建AQI多步预测模型，使用均方根误差（RMSE）对建模效果进行评估，并对测试集及其预测结果进行可视化。同时，用该模型预测附件3所给定时间的AQI，并给出每天空气质量的预警等级，其结果请用表3和表4格式在正文中具体给出。

二、问题分析

2.1 问题一思路分析

问题一要求筛选出与PM2.5浓度变化相关的因素，并说明筛选出的因素对PM2.5浓度的影响程度。为了解决这个问题，我们首先对附件1和附件2的数据进行了整合和预处理，包括缺失值处理、异常值检测和数据归一化等。然后，利用相关性分析方法计算各因素（如PM10、CO、气温、风速和降水量等）与PM2.5浓度之间的相关系数，找出与PM2.5浓度变化密切相关的因素。接下来，采用多元线性回归模型进一步分析筛选出的因素对PM2.5浓度的影响程度。通过计算回归系数和显著性检验等指标，可以得出每个因素对PM2.5浓度影响的程度和显著性水平。本研究发现，PM10和CO对PM2.5浓度影响最大，气温和风速次之，降水量对PM2.5浓度影响相对较小。

2.2 问题二思路分析

问题二要求根据附件1和附件2，构建PM2.5浓度多步预测模型，并对不同预测步长的效果进行评估。为了完成这个任务，我们首先将数据集划分为训练集和测试集。然后，基于问题一的结果，尝试了多种预测模型，如ARIMA模型、支持向量机（SVM）模型、人工神经网络（ANN）模型和长短时记忆（LSTM）神经网络模型。对比各模型在不同预测步长下的均方根误差（RMSE），选定了表现最优的LSTM模型。使用选定的模型对3步、5步、7步和12步预测效果进行了评估，并将具体结果以表1的形式给出。同时，对测试集及其预测结果进行了可视化分析，以便更直观地展示预测效果。最后，用该模型预测附件3所给定时间的PM2.5浓度，其结果以表2的形式给出。

2.3 问题三思路分析

问题三要求构建AQI多步预测模型，评估建模效果，并给出每天空气质量的预警等级。为了解决这个问题，我们首先基于问题一和问题二的结果，通过对比各模型在不同预测步长下的均方根误差（RMSE），选定了表现最优的LSTM模型。使用选定的模型对AQI进行多步预测，评估了建模效果。同时，对测试集及其预测结果进行了可视化分析，以便更直观地展示预测效果。

在完成AQI预测后，我们需要根据预测结果给出每天空气质量的预警等级。根据预警等级的划分标准，将预测得到的AQI值转化为相应的预警等级颜色。具体地，我们将AQI值分为蓝色、黄色、橙色和红色四个预警等级，并统计每个预警等级的天数。最后，将预测得到的每天空气质量预警等级以表3的形式给出，并将预警等级颜色的次数汇总结果以表4的形式给出。

三、模型假设

针对本文提出的问题，我们做了如下模型假设：

1. PM2.5 浓度受多种因素的影响，包括气象因素和污染物浓度因素
2. 气象因素包括气温、风速、相对湿度和降水量等，这些因素可以反映空气稳定度、风向和降水清洗等情况，从而影响 PM2.5 浓度。
3. 污染物浓度因素包括 PM10、SO2、NO2 等，这些污染物与 PM2.5 之间存在一定的关联性，可以通过建立多元线性回归模型进行探究。
4. 基于问题一筛选出的与 PM2.5 浓度变化有关的因素，可以建立 PM2.5 浓度预测模型，预测未来的 PM2.5 浓度。
5. 基于问题三构建的 AQI 多步预测模型，可以预测未来的 AQI 值，并根据 AQI 值的等级划分预测空气质量等级。

四、符号说明

本文常用符号见下表, 其它符号见文中说明

 

五、建模与求解

5.1 问题一的建模与求解

5.1.1 数据处理及指标的选取

数据预处理主要从以下三个方面进行：

（1）异常数据处理

在对给出的数据进行初步的统计分析发现，个别的数据点出现重复现象，经过对整条记录进行匹配确定的重复记录值删除，确保整条流量记录数据点的唯一性；在对数据进行操作时，出现了由于数据类型不一致导致的崩溃，发现在本数据集中的属性值的数据类型出现不一致性，因此为了保证数据的属性值一致的要求，将少数数据类型的数据进行数据类型转化，对无法进行数据类型转化的数据进行删除；在对数据集进行可视化展示时发现，有部分统计值值出现长时间的一致现象，为了确保数据的可用性和真实性，将该现象时间长度占比总时间长度超过五分之一的流量记录进行删除。

（2）数据记录的缺失值处理

在对数据进行数据时间点的统计时发现，数据不是连续的，为了满足时间序列本身是连续、平滑的特性，针对缺失数据进行填补。常用的缺失值填充方法，有随机填补法、均值法、中位数法、众数法等数据填充，也有 K-最近邻（KNN）、回归预测法、期望值最大化方法（EM）等建模进行数据填充方法。在考虑到本数据集缺失值比重低，且构成的时间序列的周期长等特质，对单个数据点的缺失采用前后两个序列的平均值作为缺失数据填补；对多个数据点的缺失采用多重随机插补法；对数据集中连续缺失7天以上的数据进行弃用。

（3）数据标准化

数据标准化主要是将数据按照一定的比例缩放至固定的区间范围，一方面是可以将不同维度数据特征无量纲化，另一方面是数据标准化会降低数值计算的复杂度，进一步加快模型收敛的速度以及提升模型的准确性。在大数据规模或者神经网络模型当中，数据标准化则必不可少。但是数据标准化的在实际应用并非是只有好处，数据标准化也可能会带来预测结果的偏差，主要原因是在数据标准化后的预测结果也被缩放至固定的区间范围，失去了实际的数值意义，需要通过反标准化的方法还原，而偏差就在此时产生。

数据标准化的方法常用的有两种min-max标准化和 Z-Score 标准化，根据教育数据的特性选择 Z-Score 标准化，也叫标准差标准化，主要是基于均值和标准差对数据进行标准化，该标准化方法适用于该序列中的最大值和最小值未知的情况。

我们首先对附件1和附件2数据进行合并，得到新的数据文件合并数据.xlsx直接进行数据预处理，如下代码：

import pandas as pd
import numpy as np

# 假设数据存储在名为 data.csv 的文件中
data = pd.read_excel("合并数据.xlsx")

# 删除质量等级列，因为它是分类变量，不适用于线性插值
data = data.drop(columns=["质量等级"])

# 检查缺失值的情况
print("缺失值统计：")
print(data.isnull().sum())

# 使用线性插值填充缺失值
data.interpolate(method='linear', inplace=True)

# 再次检查缺失值的情况
print("\n填充缺失值后的统计：")
print(data.isnull().sum())

# 对数据进行异常值检测和处理
def detect_outliers(data, columns, threshold=1.5):
    for column in columns:
        q1 = data[column].quantile(0.25)
        q3 = data[column].quantile(0.75)
        iqr = q3 - q1
        lower_bound = q1 - threshold * iqr
        upper_bound = q3 + threshold * iqr

        outliers = data[(data[column] < lower_bound) | (data[column] > upper_bound)]
        print(f"{column} 异常值数量：{len(outliers)}")

        # 将异常值替换为缺失值
        data[column] = data[column].apply(lambda x: np.nan if (x < lower_bound) or (x > upper_bound) else x)

# 检测并处理异常值
numeric_columns = ['AQI', 'PM10', 'O3', 'SO2', 'PM2.5', 'NO2', 'CO', 'V13305', 'V10004_700', 'V11291_700', 'V12001_700', 'V13003_700']
detect_outliers(data, numeric_columns)

# 使用线性插值填充处理后的异常值（现已变为缺失值）
data.interpolate(method='linear', inplace=True)

# 将预处理后的数据保存到新的 CSV 文件
data.to_csv("preprocessed_data.csv", index=False)

我们对其进行异常值处理和插值处理，得到新的文件preprocessed_data.csv

5.1.2 数据可视化及结果

我们对处理后的数据文件进行可视化处理，需要用到python中Matplotlib和Seaborn库，得到时间序列图、箱线图和相关性矩阵热力图，并且，我们通过计算各变量与 PM2.5 浓度的相关系数来筛选出与 PM2.5 浓度变化相关的因素。相关系数的取值范围在 -1 到 1 之间，接近 1 表示正相关，接近 -1 表示负相关，接近 0 表示无关。

我们输入如下代码：

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np

data = pd.read_csv("preprocessed_data.csv")

# 计算 PM2.5 与其他变量的相关系数
correlations = data.corr()['PM2.5'].sort_values(ascending=False)

# 打印相关系数
print(correlations)

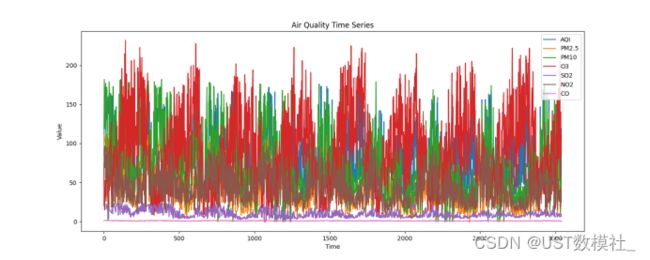
# 绘制 AQI、PM2.5、PM10、O3、SO2、NO2 和 CO 的时间序列图
plt.figure(figsize=(15, 6))
plt.plot(data["AQI"], label="AQI")
plt.plot(data["PM2.5"], label="PM2.5")
plt.plot(data["PM10"], label="PM10")
plt.plot(data["O3"], label="O3")
plt.plot(data["SO2"], label="SO2")
plt.plot(data["NO2"], label="NO2")
plt.plot(data["CO"], label="CO")
plt.xlabel("Time")
plt.ylabel("Value")
plt.title("Air Quality Time Series")
plt.legend()
plt.show()

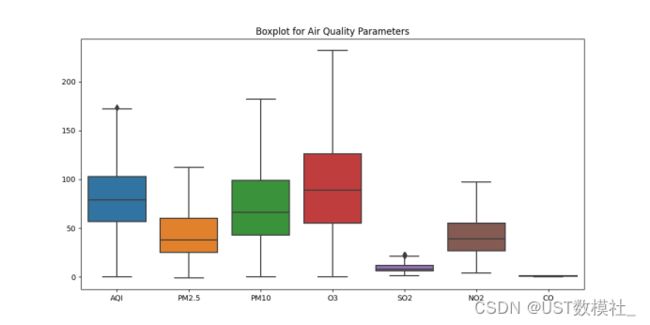
# 绘制 AQI、PM2.5、PM10、O3、SO2、NO2 和 CO 的箱型图，以查看每种污染物的分布情况
plt.figure(figsize=(12, 6))
sns.boxplot(data=data[["AQI", "PM2.5", "PM10", "O3", "SO2", "NO2", "CO"]])
plt.title("Boxplot for Air Quality Parameters")
plt.show()

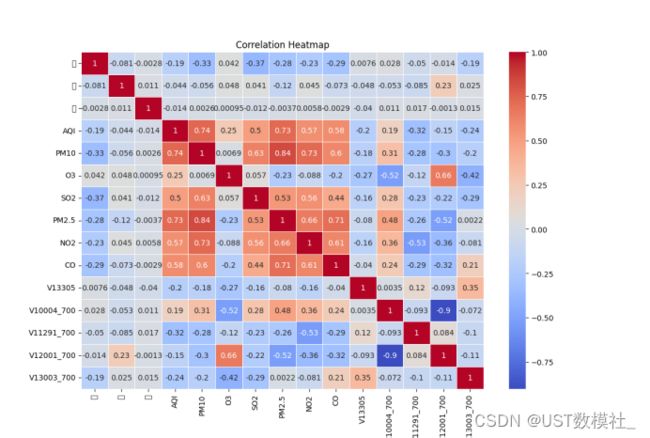
# 绘制相关性矩阵热力图
plt.figure(figsize=(12, 10))
sns.heatmap(data.corr(), annot=True, cmap="coolwarm", linewidths=0.5)
plt.title("Correlation Heatmap")
plt.show()

我们得到如下可视化图：

图5.1.1时间序列图 

 图5.1.2 箱线图

图5.1.3相关性矩阵热力图

并且我们得到如下结果表：↓↓↓