22.实战:Kaggle房价预测
1. 下载和缓存数据集
这里我们实现几个函数来方便下载数据。 首先,我们建立字典DATA_HUB, 它可以将数据集名称的字符串映射到数据集相关的二元组上, 这个二元组包含数据集的url和验证文件完整性的sha-1密钥。 所有类似的数据集都托管在地址为DATA_URL的站点上。
import hashlib
import os
import tarfile
import zipfile
import requests
#@save
DATA_HUB = dict()
DATA_URL = 'http://d2l-data.s3-accelerate.amazonaws.com/'
下面的download函数用来下载数据集, 将数据集缓存在本地目录(默认情况下为…/data)中, 并返回下载文件的名称。 如果缓存目录中已经存在此数据集文件,并且其sha-1与存储在DATA_HUB中的相匹配, 我们将使用缓存的文件,以避免重复的下载。
def download(name, cache_dir=os.path.join('.', 'data')): #@save
"""下载一个DATA_HUB中的文件,返回本地文件名"""
assert name in DATA_HUB, f"{name} 不存在于 {DATA_HUB}"
url, sha1_hash = DATA_HUB[name]
os.makedirs(cache_dir, exist_ok=True)
fname = os.path.join(cache_dir, url.split('/')[-1])
if os.path.exists(fname):
sha1 = hashlib.sha1()
with open(fname, 'rb') as f:
while True:
data = f.read(1048576)
if not data:
break
sha1.update(data)
if sha1.hexdigest() == sha1_hash:
return fname # 命中缓存
print(f'正在从{url}下载{fname}...')
r = requests.get(url, stream=True, verify=True)
with open(fname, 'wb') as f:
f.write(r.content)
return fname
我们还需实现两个实用函数: 一个将下载并解压缩一个zip或tar文件, 另一个是将本书中使用的所有数据集从DATA_HUB下载到缓存目录中。
def download_extract(name, folder=None): #@save
"""下载并解压zip/tar文件"""
fname = download(name)
base_dir = os.path.dirname(fname)
data_dir, ext = os.path.splitext(fname)
if ext == '.zip':
fp = zipfile.ZipFile(fname, 'r')
elif ext in ('.tar', '.gz'):
fp = tarfile.open(fname, 'r')
else:
assert False, '只有zip/tar文件可以被解压缩'
fp.extractall(base_dir)
return os.path.join(base_dir, folder) if folder else data_dir
def download_all(): #@save
"""下载DATA_HUB中的所有文件"""
for name in DATA_HUB:
download(name)
2.访问和读取数据集
注意,竞赛数据分为训练集和测试集。 每条记录都包括房屋的属性值和属性,如街道类型、施工年份、屋顶类型、地下室状况等。 这些特征由各种数据类型组成。 例如,建筑年份由整数表示,屋顶类型由离散类别表示,其他特征由浮点数表示。 这就是现实让事情变得复杂的地方:例如,一些数据完全丢失了,缺失值被简单地标记为“NA”。 每套房子的价格只出现在训练集中(毕竟这是一场比赛)。 我们将希望划分训练集以创建验证集,但是在将预测结果上传到Kaggle之后, 我们只能在官方测试集中评估我们的模型。
开始之前,我们将使用pandas读入并处理数据。 因此,在继续操作之前,我们需要确保已安装pandas。
# 如果没有安装pandas,请取消下一行的注释
# !pip install pandas
%matplotlib inline
import numpy as np
import pandas as pd
import torch
from torch import nn
from d2l import torch as d2l
为方便起见,我们可以使用上面定义的脚本下载并缓存Kaggle房屋数据集。
DATA_HUB['kaggle_house_train'] = ( #@save
DATA_URL + 'kaggle_house_pred_train.csv',
'585e9cc93e70b39160e7921475f9bcd7d31219ce')
DATA_HUB['kaggle_house_test'] = ( #@save
DATA_URL + 'kaggle_house_pred_test.csv',
'fa19780a7b011d9b009e8bff8e99922a8ee2eb90')
我们使用pandas分别加载包含训练数据和测试数据的两个CSV文件。
train_data = pd.read_csv(download('kaggle_house_train'))
test_data = pd.read_csv(download('kaggle_house_test'))
训练数据集包括1460个样本,每个样本80个特征和1个标签, 而测试数据集包含1459个样本,每个样本80个特征。
print(train_data.shape)
print(test_data.shape)
让我们看看前四个和最后两个特征,以及相应标签(房价)。
print(train_data.iloc[0:4, [0, 1, 2, 3, -3, -2, -1]])
我们可以看到,在每个样本中,第一个特征是ID, 这有助于模型识别每个训练样本。 虽然这很方便,但它不携带任何用于预测的信息。 因此,在将数据提供给模型之前,我们将其从数据集中删除。
# 去掉train_data的第一列(id)和最后一列(标号)和test_data的第一列(id)
# 获取到所有特征
# 一行是一个样本,每一列是特征值
all_features = pd.concat((train_data.iloc[:, 1:-1], test_data.iloc[:, 1:]))
concat函数
3. 数据预处理
如上所述,我们有各种各样的数据类型。 在开始建模之前,我们需要对数据进行预处理。
3.1 处置数值特征以及na
首先,我们将所有缺失的值替换为相应特征的平均值。然后,为了将所有特征放在一个共同的尺度上, 我们通过将特征重新缩放到零均值和单位方差来标准化数据:
# 如果all_features.dtypes != 'object',如果不是object,那么就是数值
# pandas中的object是python中的str
# 就得到数值的index
numeric_features = all_features.dtypes[all_features.dtypes != 'object'].index
# 对数值特征apply操作:(一列中每个数据 - 这一列数据的均值)/ 这一列数据的标准差
# 我们之前使用了concat把训练数据和测试数据纵向拼接了,所以这里对这两个数据集都进行了处理
# 但是在实际应用中,归一化(normalization)应该统一用 train set的均值和方差
# 实际中应该把train set的均值和方差用到测试集上
# 归一化不应该用训练集和测试集的期望和方差,这里只不过是把官方的训练和测试集统一变成了训练集
all_features[numeric_features] = all_features[numeric_features].apply(
lambda x: (x-x.mean()) / (x.std())) # 均值方差归一化 :把所有数据归一到均值为0方差为1 的分布中
# 把not a number改成0,因为均值为0,所以这里把na变成0也就是变成了均值
all_features[numeric_features] = all_features[numeric_features].fillna(0)
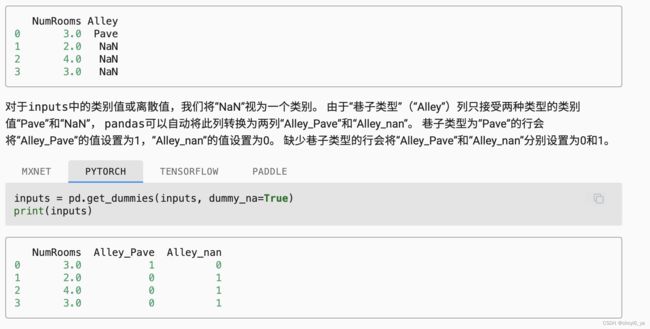
2. 处理离散值。
这包括诸如“MSZoning”之类的特征。 我们用独热编码替换它们, 方法与前面将多类别标签转换为向量的方式相同 。 例如,“MSZoning”包含值“RL”和“Rm”。 我们将创建两个新的指示器特征“MSZoning_RL”和“MSZoning_RM”,其值为0或1。 根据独热编码,如果“MSZoning”的原始值为“RL”, 则:“MSZoning_RL”为1,“MSZoning_RM”为0。 pandas软件包会自动为我们实现这一点。
all_features = pd.get_dummies(all_features,dummy_na = True)
all_features.shape
从运行结果可以看出特征变多了,从之前79变成331,原因是把离散值做成了one-hot encoding:
![]()
如果处理字符串该怎么办呢?
答:使用one-hot encoding,假设一列中有5个不同的值,就创建5个feature,也就是把一列等价于变成5列,然后对应的列置为1,其余的四列为0。具体,可以看 这篇文章:pandas.get_dummies 的用法
4. 转换为张量格式
最后,通过values属性,我们可以 从pandas格式中提取NumPy格式,并将其转换为张量表示用于训练。
n_train = train_data.shape[0] # 获得训练样本的数量
# 通过切片操作,把训练特征选出来
train_features = torch.tensor(all_features[:n_train].values,
dtype = torch.float32)
# 把测试特征选出来
test_features = torch.tensor(all_features[n_train:].values,
dtype = torch.float32)
# 把标签转成一个列向量
train_labels = torch.tensor(train_data.SalePrice.values.reshape(-1,1),
dtype = torch.float32)
5. 训练
首先,我们训练一个带有损失平方的线性模型。 显然线性模型很难让我们在竞赛中获胜,但线性模型提供了一种健全性检查, 以查看数据中是否存在有意义的信息。 如果我们在这里不能做得比随机猜测更好,那么我们很可能存在数据处理错误。 如果一切顺利,线性模型将作为基线(baseline)模型, 让我们直观地知道最好的模型有超出简单的模型多少。
loss = nn.MSELoss() # 平方损失
# 对于二维张量,shape[0]代表行数,shape[1]代表列数
in_features = train_features.shape[1] # 获取到了训练特征的列数(311)
def get_net():
# 单层的线性回归,w矩阵有311行,1列
net = nn.Sequential(nn.Linear(in_features,1))
return net

ps:一般y取log以后会更接近正态分布,用回归性质会比较好
def log_rmse(net,features,labels):
# clamp的作用是限幅。将input的值限制在[1, inf]之间,并返回结果
# 为了在取对数时进一步稳定该值,将小于1的值设置为1
# net(features)就是令输入经过net得到的输出,clamp对输出进行了限幅
clipped_preds = torch.clamp(net(features),1,float('inf'))
# 计算相对误差:
# 将预测的输出和真实label 做了log计算后
# 再丢到MSE中,再开根号
rmse = torch.sqrt(loss(torch.log(clipped_preds),torch.log(labels)))
# .item():将Tensor变量转换为python标量(int float等)
return rmse.item()
PyTorch:torch.clamp()用法详解
与前面的部分不同,我们的训练函数将借助Adam优化器 (我们将在后面章节更详细地描述它)。 Adam优化器的主要吸引力在于它对初始学习率不那么敏感。
通过下面的train函数,是训练参数模型w和b。
def train(net,train_features,train_labels,test_features,test_labels,
num_epochs,learning_rate,weight_decay,batch_size):
train_ls,test_ls = [],[]
# 把真实数据features和labels做成tuple,传入到函数
train_iter = d2l.load_array((features,labels),batch_size)
optimizer = torch.optim.Adam(net.parameters(),lr = learning_rate,
weight_decay = weight_decay)
for epoch in range(num_epochs):
# 一次for循环,就是从训练数据迭代器中取batch_size数据来学习参数w和b
for X,y in train_iter:
optimizer.zero_grad()
l = loss(net(X),y)
l.backward()
optimizer.step()
# 学习到了w和b之后,再把训练数据放入net中,计算预测数据以及真实标签的相对误差
train_ls.append(log_rmse(net,train_features,train_labels))
if test_labels is not None:
# 学习到了w和b之后,再把测试数据放入net中,计算预测数据以及真实标签的相对误差
test_ls.append(log_rmse(net,test_features,test_labels))
return train_ls, test_ls
6. K折交叉验证(选择超参数)
它有助于模型选择和超参数调整。
我们首先需要定义一个函数,在K折交叉验证过程中返回第i折的数据。 具体地说,它选择第i个切片作为验证数据,其余部分作为训练数据。 注意,这并不是处理数据的最有效方法,如果我们的数据集大得多,会有其他解决办法。
def get_k_fold_data(k,i,X,y):
assert k>1 # 如果k>1,则程序向下执行,否则会抛出AssertionError错误
# 每一折的样本数量
fold_size = X.shape[0] // k
X_train,y_train = None,None
for j in range(k):
# slice()中输入2个参数,分别为起始位置和终止位置,左闭右开
# 第一轮j=0,返回数组[0,..,fold_size-1]
# 第二轮j=1,返回[fold_size,fold_size*2-1],以此类推
idx = slice(j*fold_size,(j+1)*fold_size)
# X[idx,:] 把对应的样本取出来,y[idx]把对应的标签取出来
X_part,y_part = X[idx,:],y[idx]
# i表示当前第i折
if j == i:
X_valid,y_valid = X_part,y_part
# 如果X_train是None,就表示之前还没存数据,就存下来作为训练集
elif X_train is None:
X_train,y_train = X_part,y_part
# 之前X_train就存了数据的话,就concat当前这一part
else:
# 将两个张量(tensor)按指定维度拼接在一起
X_train = torch.cat([X_train,X_part],dim=0)
y_train = torch.cat([y_train,y_part],dim=0)
return X_train,y_train,X_valid,y_valid
当我们在K折交叉验证中训练K次后,返回训练和验证误差的平均值。
def k_fold(k,X_train,y_train,num_epochs,learning_rate,weight_decay,
batch_size):
train_l_sum,valid_l_sum = 0,0 # 训练损失和,以及,验证损失和
for i in range(k):
# 第i块作为验证数据集
data = get_k_fold_data(k,i,X_train,y_train)
net = get_net # net是单层的线性回归
train_ls,valid_ls = train(net,*data,num_epochs,learning_rate,
weight_decay,batch_size)
# train_ls[-1]返回每一折的最后一次epoch的损失值
train_l_sum += train_ls[-1]
valid_l_sum += valid_ls[-1]
if i == 0:
d2l.plot(list(range(1, num_epochs + 1)), [train_ls, valid_ls],
xlabel='epoch', ylabel='rmse', xlim=[1, num_epochs],
legend=['train', 'valid'], yscale='log')
print(f'折{i + 1},训练log rmse{float(train_ls[-1]):f}, '
f'验证log rmse{float(valid_ls[-1]):f}')
return train_l_sum / k,valid_l_sum / k
7. 模型选择
在本例中,我们选择了一组未调优的超参数,需要进行改进模型。 找到一组调优的超参数可能需要时间,这取决于一个人优化了多少变量。 有了足够大的数据集和合理设置的超参数,K折交叉验证往往对多次测试具有相当的稳定性。 然而,如果我们尝试了不合理的超参数,我们可能会发现验证效果不再代表真正的误差。
k, num_epochs, lr, weight_decay, batch_size = 5, 100, 5, 0, 64
train_l, valid_l = k_fold(k, train_features, train_labels, num_epochs, lr,
weight_decay, batch_size)
print(f'{k}-折验证: 平均训练log rmse: {float(train_l):f}, '
f'平均验证log rmse: {float(valid_l):f}')
请注意,有时一组超参数的训练误差可能非常低,但K折交叉验证的误差要高得多, 这表明模型过拟合了。 在整个训练过程中,我们希望监控训练误差和验证误差这两个数字。 较少的过拟合可能表明现有数据可以支撑一个更强大的模型, 较大的过拟合可能意味着我们可以通过正则化技术来获益。
8. 提交Kaggle预测
def train_and_pred(train_features,test_features,train_labels,test_data,
num_epochs,lr,weight_decay,batch_size):
net = get_net()
train_ls,_ = train(net,train_features,train_labels,None,None,
num_epochs,lr,weight_decay,batch_size)
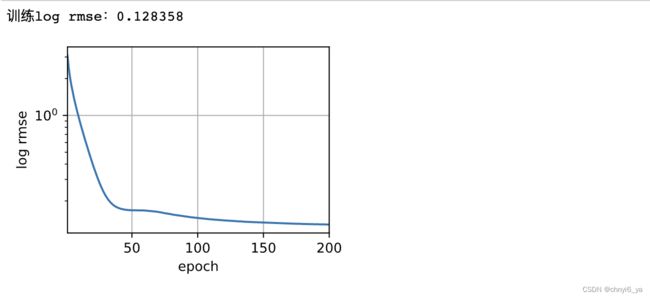
d2l.plot(np.arange(1, num_epochs + 1), [train_ls], xlabel='epoch',
ylabel='log rmse', xlim=[1, num_epochs], yscale='log')
print(f'训练log rmse:{float(train_ls[-1]):f}')
# 将网络应用于测试集。
preds = net(test_features).detach().numpy()
# 将其重新格式化以导出到Kaggle
test_data['SalePrice'] = pd.Series(preds.reshape(1, -1)[0])
submission = pd.concat([test_data['Id'], test_data['SalePrice']], axis=1)
submission.to_csv('submission.csv', index=False)
如果测试集上的预测与K倍交叉验证过程中的预测相似, 那就是时候把它们上传到Kaggle了。 下面的代码将生成一个名为submission.csv的文件。
train_and_pred(train_features, test_features, train_labels, test_data,
num_epochs, lr, weight_decay, batch_size)