计算机图形学与opengl C++版 学习笔记 第13章 几何着色器
目录
- 13.1 OpenGL中的逐个图元处理
- 13.2 修改图元
- 13.3 删除图元
- 13.4 添加图元
- 13.5 更改图元类型
- 补充说明
在OpenGL管线中,紧跟着曲面细分阶段的是几何阶段。在这一阶段中,程序员可以选择包含几何着色器。这个阶段实际上在曲面细分阶段出现之前就已经存在,它在3.2版本(2009年)成为OpenGL核心的一部分。
与曲面细分一样,几何着色器使程序员能够以顶点着色器中无法实现的方式操纵顶点组。在某些情况下,可以使用曲面细分着色器或者几何着色器完成同样的任务,因为它们的功能在某些方面重叠。
13.1 OpenGL中的逐个图元处理
几何着色器阶段位于曲面细分和光栅化之间,位于用于图元处理的管线段内(见图2.2)。顶点着色器允许一次操作一个顶点,而片段着色器一次可以操作一个片段(实际上是一个像素),但几何着色器却可以一次操作一个图元。
回想一下,图元是OpenGL中绘制对象的基本元件。只有少数几种类型的图元;我们将主要关注操纵三角形图元的几何着色器。因此,当我们说几何着色器可以一次操作一个图元时,我们通常意味着着色器一次可以访问三角形的3个顶点。几何着色器允许一次性访问图元中的所有顶点,然后:
- 输出相同的图元保持不变;
- 输出修改了顶点位置的相同类型图元;
- 输出不同类型的图元;
- 输出更多的其他图元;
- 删除图元(根本不输出)。
与曲面细分评估着色器类似,可以在几何着色器中将传入的顶点属性作为数组进行访问。但是,在几何着色器中,传入属性数组仅索引到图元尺寸那么大。例如,如果图元是三角形,则可用索引为0、1、2。使用预先定义的数组gl_in访问顶点数据本身,如下所示。
gl_in[2].gl_Position // 第三个顶点的位置
与曲面细分评估着色器类似,几何着色器输出的顶点属性都是标量。也就是说,输出是形成图元的各个顶点(它们的位置和其他属性变量,如果有的话)的流。
有一个布局修饰符用于设置图元输入/输出类型和输出大小。特殊的GLSL命令EmitVertex()指定了将要输出一个顶点。特殊的GLSL命令EndPrimitive()表示一个特定的图元构建完成。
有一个内置变量gl_PrimitiveIDIn,它保存当前图元的ID。ID从0开始,并计数到图元总数减1。
我们将探讨四种常见的操作类型:
- 修改图元;
- 删除图元;
- 添加图元;
- 更改图元类型。
13.2 修改图元
当通过对图元(通常为三角形)的单独更改就可以影响对象形状的改变时,使用几何着色器就很方便。
例如,考虑我们之前在图7.12中呈现的环面。假设环面代表内部的空间(例如当表示轮胎时),而我们想要给它“充气”。简单地在 C++/OpenGL代码中应用比例缩放因子将无法实现这一点,因为它的基本形状不会改变。想要让其显示出“充气”的外观,还需要在环面伸入空的中心空间时使内孔变小。
解决这个问题的一种方法是将表面法向量添加到每个顶点。虽然这可以在顶点着色器中完成,但是我们在几何着色器中进行练习。程序13.1显示了GLSL几何着色器的代码。其他模块与程序7.3相同,只有一些小改动:片段着色器输入名称现在需要反映几何着色器的输出(例如,varyingNormal变为varyingNormalG),C++/OpenGL应用程序需要编译几何着色器并在链接之前将其附加到着色器程序。新着色器被指定为几何着色器,如下所示。
GLuint gShader = glCreateShader(GL_GEOMETRY_SHADER);
在程序13.1中需要注意,与顶点着色器的输出变量对应的输入变量被声明为数组。这为程序员提供了一种机制,可以使用索引0、1和2访问三角形图元中的每个顶点及其属性。我们希望沿着它们的表面法向量向外移动这些顶点。在顶点着色器中,顶点和法向量都已经被转换到视图空间。我们为每个传入的顶点位(gl_in[i].gl_Position)添加法向量的一小部分,然后将投影矩阵应用于结果,生成每个输出gl_Position。
值得注意的是,使用GLSL调用EmitVertex()来指定我们何时完成了计算输出gl_Position及其相关的顶点属性并准备输出顶点。 EndPrimitive()调用指定我们已经完成了组成图元(在本例中为三角形)的一组顶点的定义。结果如图13.1所示。
几何着色器包括两个布局限定符。第一个指定输入图元类型,并且必须与C++端glDrawArrays()或glDrawElements()调用中的图元类型兼容。选项如表13.1所示。
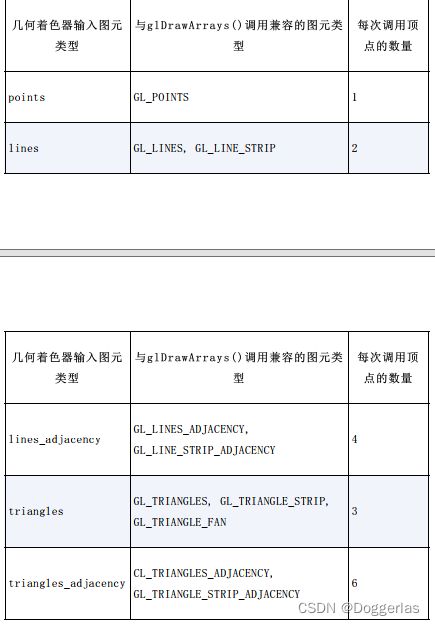
各种OpenGL图元类型(包括“strip”和“fan”类型)在第4章中讲过。“相邻”类型在OpenGL中用来与几何着色器一起使用,并且它们可以访问与图元相邻的顶点。我们在本书中不使用它们,但为了完整性,依然列出它们。
输出图元类型必须是points、line_strip或triangle_strip。请注意,输出布局限定符也会指定着色器在每次调用中输出的最大顶点数。
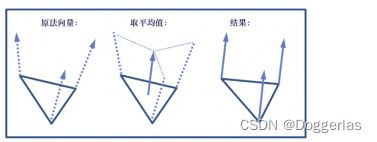
在顶点着色器中可以更容易地对环面进行这种特定的改变。然而,假设不是沿着自己的表面法向量向外移动每个顶点,而是希望将每个三角形沿其表面法向量向外移动,实际上是将环面的组成三角形向外“爆炸”。顶点着色器做不到这一点,因为计算三角形的法向量
需要对3个三角形顶点的顶点法向量进行平均,并且顶点着色器一次只能访问三角形中一个顶点的顶点属性。但是,我们可以在几何着色器中执行此操作,因为几何着色器可以访问每个三角形中的所有3个顶点。我们平均它们的法向量来计算三角形的曲面法向量,然后将该平 均法向量加给三角形图元中的每个顶点。图13.2、图13.3和图13.4分 别显示了曲面法向量的平均值、修改后的几何着色器main()代码和输 出的结果。
通过确保环面的内部也是可见的(通常这些三角形会被OpenGL剔除,因为它们是“背面”),可以改善“爆炸”环面的外观。一种解决方式是使环面被渲染两次,一次以正常方式进行,一次使缠绕顺序反转(使缠绕顺序反转实际上相当于切换哪些面朝向前方,哪些面朝向后方)。我们还向着色器(通过统一变量)发送一个标志,以禁用背向三角形上的漫反射和镜面光,以使它们不那么突出。代码的更改如下。
对display()函数的修改:
对片段着色器的修改:
13.3 删除图元
几何着色器的一个常见用途是通过合理地删除一些图元来从简单的对象构建丰富的装饰对象。例如,从我们的环面中移除一些三角形可以将其变成一种复杂的格子结构,而从零开始建模这个结构是更加困难的。执行此操作的几何着色器显示在程序13.2中,输出如图13.6所示。

程序13.2 几何着色器:删除图元

不需要对代码进行其他更改。请注意这里使用了mod函数——所有顶点,除了每3个图元中的第一个图元的顶点被忽略之外,都被传递。 在这里,渲染背向三角形也可以提高真实感,如图13.7所示。

13.4 添加图元
也许几何着色器最有趣和最有用的用途是为正在渲染的模型添加额外的顶点和/或图元。这使得可以进行诸如增加对象中的细节以改善高度贴图,或者完全改变对象的形状之类的事情。
考虑以下示例,我们将环面中的每个三角形更改为一个微小的三角形金字塔。
我们的策略类似于我们之前的“爆炸”环面示例,如图13.8所示。传入三角形图元的顶点用于定义金字塔的基座。金字塔的壁由那些顶点和通过平均原始顶点的法向量计算的新点(称为“尖峰点”)构成。然后通过从尖峰点到基座的两个向量的叉积计算金字塔的3个“边”中的每一个的新法向量。
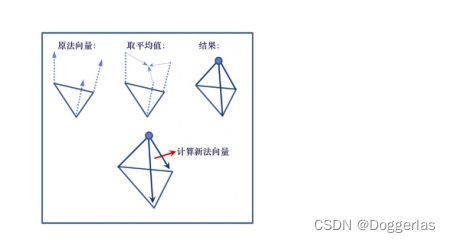
程序13.3中的几何着色器为环面中的每个三角形图元执行此操作。对于每个输入三角形,它输出3个三角形图元,总共9个顶点。每个新三角形都在函数makeNewTriangle()中构建,该函数被调用3次。 它计算指定三角形的法向量,然后调用函数setOutputValues()为发出的每个顶点分配适当的输出顶点属性。在发出所有3个顶点之后,它调用EndPrimitive()。为了确保准确地执行光照,为每个新创建的顶点计算光照方向向量的新值。
结果输出如图13.9所示。如果尖峰长度(sLen)变量增加,则添加的表面“金字塔”将更高。然而,在没有阴影的情况下,它们可能看起来并不真实。将阴影贴图添加到程序13.3留作练习。
仔细应用这种技术可以模拟尖峰、荆棘和其他精细表面突起,或者反向的压痕、凹坑(参考资料[DV14, TR13, KS16])等。
13.5 更改图元类型
OpenGL允许在几何着色器中更改图元类型。此功能的一个常见用途是将输入三角形转换为一个或多个输出线段,来模拟毛发或头发。 虽然生成令人信服的头发仍然是更难的现实世界项目之一,但几何着色器可以在许多情况下帮助实现实时渲染。
程序13.4显示了一个几何着色器,它将每个输入的3个顶点的三角形转换为一个向外的两个顶点的线段。它首先通过平均三角形顶点位置生成三角形的质心,来计算头发束的起点。然后它使用和程序13.3中相同的“尖峰点”作为头发的终点。输出图元被指定为具有两个顶点的线段,第一个顶点是起点,第二个顶点是终点。结果显示在图13.10中,用于实例化维数为72个切片的环面。
当然,这仅仅是产生完全逼真头发的起点。使头发弯曲或移动将需要若干修改,例如为线条生成更多顶点并沿曲线计算它们的位置和/或结合随机性。由于线段没有明显的表面法向量,光照会很复杂;在这个例子中,我们简单地指定法向量与原始三角形的表面法向量相同。
程序13.4 几何着色器:改变图元类型
补充说明
几何着色器吸引人的一点在于它们相对容易使用。虽然几何着色器的许多应用可以使用曲面细分来实现,但几何着色器的机制通常使它们更容易实现和调试。当然,几何与曲面细分的相对适用范围取决于特定的应用。
生成令人信服的真实头发或毛发具有挑战性,并且根据应用场景需要采用多种技术。在某些情况下,简单的纹理就足够了,或者可以使用曲面细分或几何着色器,例如本章所示的基本技术。当需要更真实的效果时,移动(动画)和光照变得棘手。头发和毛发生成的两个专用工具是HairWorks和TressFX。HairWorks是NVIDIA GameWorks套件[GW18]的一部分,而TressFX是由AMD开发的[TR18]。前者适用于OpenGL和DirectX,而后者仅适用于DirectX。使用TressFX的例子可以在[GP14]中找到。