计算机图形学与opengl C++版 学习笔记 第14章 其他技术

在本章中，我们将使用在本书中学到的工具来探索各种技术。有些我们会完全讲解，而其他一些我们将只会粗略描述。图形编程是一 个巨大的领域，本章绝不是全面的，而是介绍了多年来发展的一些创造性效果。

14.1 雾

通常当人们想到雾时，他们会想到有雾的早晨，能见度很低。事实上，大气雾霾（如雾）比我们大多数人认为的更常见。大多数时候，空气中都会有一定程度的雾霾，我们已经习惯于看到它，通常不会意识到它的存在，所以我们可以通过引入雾来增强我们室外场景的真实感——即使只是少量。

雾也可以增强深度感。近处物体比远处物体具有更高的清晰度，对于我们的大脑是可以用来破译3D场景的地形结构的另一个视觉提示。

模拟雾的方法有很多种，从非常简单的模型到包含光散射效应的复杂模型。即使非常简单的方法也是有效的。有一种方法是基于物体距眼睛的距离将实际像素颜色与另一种颜色（“雾”的颜色通常是灰色或蓝灰色——也用于背景颜色）混合。

图14.1（见彩插）说明了这个概念。眼睛（相机）显示在左侧，两个红色物体放置在视锥体中。圆柱体更靠近眼睛，所以它主要是原始颜色（红色）；立方体远离眼睛，所以它主要是雾色。对于这个简单的实现，几乎所有的计算都可以在片段着色器中执行。

图14.1 雾：基于距离的混合

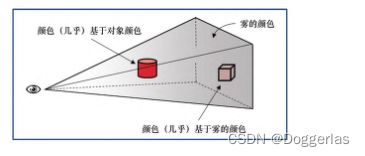
程序14.1显示了一个非常简单的雾算法的相关代码，该算法按照从相机到像素的距离，使用从对象颜色到雾颜色的线性混合。具体来说，此示例将雾添加到程序10.4中的高度贴图示例。

程序14.1 简单的雾生成

变量fogColor指定雾的颜色。变量fogStart和fogEnd指定输出颜色从对象颜色过渡到雾色的范围（在视觉空间中），并且可以调整以满足场景的需要。在对象颜色中混合的雾的百分比在变量fogFactor中计算，该变量是顶点与fogEnd的接近程度与过渡区域的总长度之比。 GLSL的clamp()函数用于将此比率限制在值0.0和1.0之间。然后，GLSL 的mix()函数根据fogFactor的值返回雾颜色和对象颜色的加权平均值。图14.2（见彩插）展示了向具有高度贴图地形的场景添加雾（[LU16]的岩石纹理也已应用）。

图14.2 雾的例子

14.2 复合、混合、透明度

我们已经看到了一些混合的例子，比如第7章的补充说明以及我们刚才实现的雾。但是，我们还没有看到如何在像素操作期间利用片段着色器之后的混合（或合成）功能（回想一下图2.2所示的管线序列）。透明度在那个步骤被处理，我们现在来了解一下。

在本书中，我们经常使用vec4数据类型来表示齐次坐标系中的3D点和向量。您可能已经注意到我们还经常使用vec4来存储颜色信息，其中前3个值由红色、绿色和蓝色组成，那么第四个元素是什么？

颜色中的第四个元素称为Alpha通道，用来指定颜色的不透明度。 不透明度是衡量像素颜色不透明程度的指标。Alpha值为0表示“无不 透明度”或完全透明。Alpha值为1表示“不透明度满值”，也就是完全不透明。在某种意义上，颜色的“透明度”是1−α，其中α是Alpha通道的值。

回忆一下第2章，像素操作利用Z缓冲区，当发现另一个对象在该像素的位置更近时，通过替换现有的像素颜色来实现隐藏面消除。我们实际上可以更好地控制这个过程——可以选择混合两个像素。

当渲染一个像素时，它被称为“源”像素。已经在帧缓冲器中的像素（可能是从先前的对象渲染得来）被称为“目标”像素。OpenGL 提供了许多选项，用于决定最终将两个像素中的哪一个或者它们的组合，放置在帧缓冲区中。请注意，像素操作步骤不是可编程阶段——因此用于配置所需合成的OpenGL工具可在C++应用程序中（而不是在着 色器中）找到。

用于控制合成的两个OpenGL函数是glBlendEquation(mode)和glBlendFunc(srcFactor, destFactor)。图14.3显示了合成过程的概述。

图14.3 OpenGL合成概述

合成过程的工作过程如下。

（1）源像素和目标像素分别乘以源因子和目标因子。源和目标因子在blendFunc()函数调用中指定。

（2）然后使用指定的blendEquation来组合修改后的源像素和目标像素以生成新的目标颜色。混合方程在glBlendEquation()调用中指定。

glBlendFunc()参数的常见选项（即srcFactor和destFactor）如表14.1所示。

表14 .1 glB lend Func()参数的常见选项

那些用到blendColor（GL_CONSTANT_COLOR等）的选项需要额外调用glBlendColor()来指定将用于计算混合函数结果的常量颜色。 还有一些其他混合函数未在表14.1中显示。

glBlendEquation()参数（混合模式）的可能选项如表14.2所示。

表14 .2 glB lend E quation()参数的可能选项

glBlendFunc()默认设置srcFactor为GL_ONE（1.0），destFactor 为GL_ZERO（0.0）。glBlendEquation()的默认值为GL_FUNC_ADD。因此，在默认情况下，源像素不变（乘以1），目标像素被按比例缩小到0，并且两者相加意味着源像素变为帧缓冲区的颜色。

还有命令glEnable(GL_BLEND)和glDisable(GL_BLEND)，它们可用于告诉OpenGL应用指定的混合，或忽略它。

我们不会在这里说明所有选项的效果，但我们将介绍一些说明性示例。假设我们在C++/OpenGL应用程序中指定以下设置：

glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA)
glBlendEquation(GL_FUNC_ADD)

合成将如下进行。

（1）源像素按其Alpha值缩放。
（2）目标像素按1−srcAlpha（源透明度）缩放。
（3）像素值加在一起。

例如，如果源像素为红色，具有75%不透明度，即[1,0,0,0.75]， 并且目标像素包含完全不透明的绿色，即[0,1,0,1]，则结果放在帧缓冲区将是：

srcPixel * srcAlpha = [0.75, 0, 0, 0.5625]
destPixel * (1-srcAlpha) = [0, 0.25, 0, 0.25]
resulting pixel = [0.75, 0.25, 0, 0.8125]

也就是说，主要是红色，有些是绿色的，而且基本上是实色。这个设置的总体效果是让目标像素以与源像素的透明度相对应的量显示。在此示例中，帧缓冲区中的像素为绿色，输入像素为红色，透明 度为25%（不透明度为75%）。因此允许一些绿色通过红色显示。

事实证明，混合函数和混合方程的这些设置在许多情况下都能很 好地工作。我们将它们应用到包含两个3D模型的场景中的实际示例中去：一个环面和环面前的金字塔。图14.4显示了这样一个场景，左边是一个不透明的金字塔，右边是金字塔的Alpha值设置为0.8。光照已经添加。

对于许多应用——例如创建平面“窗口”作为房屋模型的一部分，这种简单的透明度实现可能就足够了。但是，在图14.4所示的示例中，存在相当明显的不足之处。尽管金字塔模型现在实际上是透明的，但实际透明的金字塔不仅应该显示其背后的对象，还应该显示其自身的背面。

图14.4 金字塔的Alpha = 1.0（左），Alpha = 0.8（右）

实际上，金字塔的背面没有出现的原因是因为我们启用了背面剔除。一个合理的想法可能是在绘制金字塔时禁用背面剔除。但是，这通常会产生其他伪影，如图14.5左图所示。简单地禁用背面剔除的问题在于混合的效果取决于渲染表面的顺序（因为这决定了源像素和目标像素），并且我们不总是能够控制渲染顺序。通常有利的是首先渲染不透明对象，以及在后面的对象（例如环面），最后再渲染透明对象。这也适用于金字塔的表面，并且在这种情况下，包括金字塔底部的两个三角形看起来不同的原因是它们中的一个在金字塔的前面之前被渲染而一个在之后被渲染。诸如此类的伪影有时被称为“顺序”伪影，并且它们可以在透明模型中显示，因为我们不总是能预测其三角形将被渲染的顺序。

我们可以通过从背面开始分别渲染正面和背面来解决金字塔示例中的问题。程序14.2显示了执行此操作的代码。我们通过统一变量来指定金字塔的Alpha值并传递给着色器程序，然后通过将指定的Alpha替换为计算的输出颜色将其应用于片段着色器中。

另请注意，要使光照正常工作，我们必须在渲染背面时翻转法向量。我们通过向顶点着色器发送一个标志来完成此操作，然后我们在其中翻转法向量。

程序14.2 透明度的两遍混合

这种“两遍”解决方案的结果如图14.5右图所示。

图14.5 透明度和背面：排序伪影（左）和两遍校正（右）

虽然它在这里运行良好，但程序14.2中显示的两遍解决方案并不总是足够的。例如，一些更复杂的模型可能具有面向前方的隐藏表面，并且如果这样的对象变得透明，我们的算法将无法渲染模型的那 些隐藏的前向部分。Alec Jacobson描述了一个适用于大量案例的五遍序列[JA12]。

14.3 用户定义剪裁平面

OpenGL 不仅可以应用于视锥体，还包括了指定剪裁平面的功能。 用户定义的剪裁平面的一个用途是对模型切片。这样就可以通过从简单的模型开始并从中切片来创建复杂的形状。

剪裁平面使用平面的标准数学定义来定义：

其中a、b、c和d是用来定义有X、Y和Z轴的3D空间中特定平面的参数。参数表示垂直于平面的向量(a,b,c)以及从原点到平面的距离d。可以使用vec4在顶点着色器中指定这样的平面，如下所示：

这对应于平面：

然后，通过使用内置的GLSL变量gl_ClipDistance[ ]，可以在顶点着色器中实现裁剪，如下例所示：

gl_ClipDistance [0] = dot(clip_plane.xyz, vertPos) + clip_plane.w;

在此示例中，vertPos指的是在顶点属性（例如来自VBO）中进入顶点着色器的顶点位置，clip_plane定义如上。然后我们计算从裁剪平面到传入顶点的带符号距离（如第3章所示），如果顶点在平面上，则为0，或者取决于顶点在平面的哪一侧而为负或正。 gl_ClipDistance数组的下标允许定义多个裁剪距离（即多个平面）。 可以定义的最大用户裁剪平面数量取决于图形卡的OpenGL实现。

然后必须在C++/OpenGL应用程序中启用用户定义的裁剪。内置OpenGL标识符GL_CLIP_DISTANCE0、GL_CLIP_DISTANCE1等，对应于每个gl_ClipDistance[ ]数组元素。例如，启用第0个用户定义剪裁平面，如下所示。

glEnable(GL_CLIP_DISTANCE0);

将前面的步骤应用到我们的发光环面会产生如图14.6所示的输出，其中环面的前半部分已经被剪裁了（还应用了旋转以提供更清晰的视图）。

可能看起来好像环面的底部也被修剪了，但这是因为环面的内表面没有被渲染。当裁剪会显示形状的内部表面时，也就需要渲染它们，否则模型将显示得不完整（如图14.6所示）。

图14.6 剪裁一个环面

渲染内表面需要再次调用gl_DrawArrays()，并颠倒缠绕顺序。此外，在渲染背向三角形时，必须反转曲面法向量（如上一节所述）。 C++应用程序和顶点着色器的相关修改如程序14.3所示，输出如图14.7所示。

图14.7 带背面的剪裁

程序14.3 带背面的剪裁

14.4 3D纹理

2D纹理包含由两个变量索引的图像数据，而3D纹理包含相同类型的图像数据，但是处在由3个变量索引的3D结构中。前两个维度仍然代表纹理贴图中的宽度和高度，第三个维度代表深度。

因为3D纹理中的数据以与2D纹理类似的方式存储，所以很容易将 3D纹理视为一种3D“图像”。但是，我们通常不将3D纹理源数据称为3D图像，因为对于这种结构没有常用的图像文件格式（即没有类似的3D版JPEG，至少没有真正三维的图像）。相反，我们建议将3D纹理视为一种物质，我们将其浸没（或“浸入”）被纹理化的对象，从而使对象的表面点从纹理中的相应位置获得颜色。或者可以想象这个物体被从3D纹理“立方体”中“雕刻”出来，就像雕塑家用一块坚固的大理石雕刻出一个人物一样。

OpenGL支持3D纹理对象。为了使用它们，我们需要学习如何构建 3D纹理以及如何使用它来纹理化对象。

与可以从标准图像文件构建的2D纹理不同，3D纹理通常是在程序 上生成的。正如之前对2D纹理所做的那样，我们决定分辨率，即每个维度中的纹素数量。根据纹理中的颜色，我们可以构建包含这些颜色 的三维数组。如果纹理包含可以与各种颜色一起使用的“图案”，我们可能会建立一个保存图案的数组，例如0和1。

例如，我们可以通过填充对应于所需条纹图案的0和1的数组来构建表示水平条纹的3D纹理。假设纹理的所需分辨率是200×200×200纹 素，并且纹理由交替的条纹组成，每个条纹高10纹素。通过在嵌套循环中使用适当的0和1填充数组来构建此类结构的简单函数（假设在这种情况下，宽度、高度和深度变量均设置为200）将如下所示。

存储在tex3Dpattern数组中的图案如图14.8所示（见彩插），0呈蓝色，1呈黄色。

图14.8 条纹3D纹理图案

使用条纹图案对对象进行纹理处理，如图14.8所示，需要执行以下步骤

1. 生成如上所示的图案
2. 使用图案填充所需颜色的字节数组
3. 将字节数组加载到纹理对象中
4. 确定对象顶点的适当3D纹理坐标
5. 在片段着色器中使用适当的采样器来纹理化对象。

3D纹理的纹理坐标范围为［0…1］，与2D纹理的方式相同。有趣的是，步骤（4）（确定3D纹理坐标）通常比最初怀疑的要简单得多。事实上，它通常比2D纹理更简单！这是因为（在2D纹理的情况下）3D对象被2D图像纹理化，我们需要决定如何“展平”3D对象的顶点（例如通过UV映射）来创建纹理坐标。但是当3D纹理化时，对象和纹理都具有相同的维度。在大多数情况下，我们希望对象反映纹理图案，就像它被“雕刻”出来一样（或浸入其中）。所以顶点位置本身就是纹理坐标！通常所需的只是应用一些简单的缩放以确保对象的顶点的位置坐标映射到3D纹理坐标的范围[0,1]。

由于我们通过程序来生成3D纹理，所以我们需要一种从生成的数据中构造OpenGL纹理贴图的方法。将数据加载到纹理中的过程与我们之前在第5.12节中看到的类似。在这种情况下，我们用颜色值填充3D数组，然后将它们复制到纹理对象中。

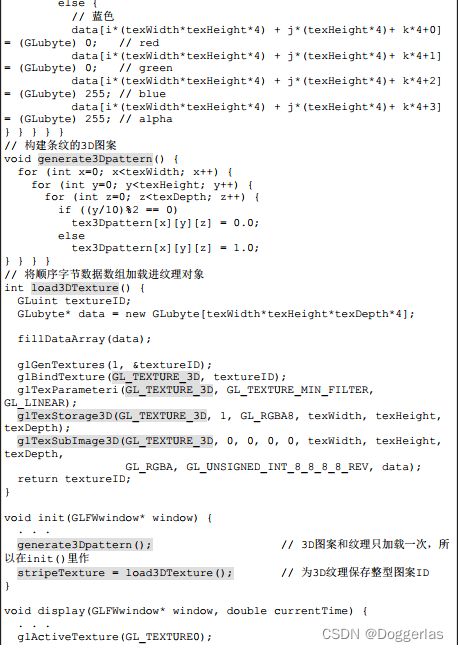
程序14.4展示出了用于实现所有先前步骤的各种组件，以便使用程序构建的3D纹理来纹理化具有蓝色和黄色水平条纹的对象。所需的图案在generate3Dpattern()函数中构建，该函数将图案存储在名为 “tex3Dpattern”的数组中。然后在函数fillDataArray()中构建“图像”数据，按照图案，该函数使用与RGB颜色R、G、B和A相对应的字节数据填充3D数组，每个数据在[0,255]范围内。然后将这些值复制到 load3DTexture()函数中的纹理对象中。

程序14.4 3D纹理：条纹图案

在C++/OpenGL应用程序中，load3Dtexture()函数将生成的数据加载到3D纹理中。它不使用SOIL2来加载纹理，而是直接进行相关的 OpenGL调用，其方式类似于前面5.12节中所述的方式。图像数据应该被格式化为对应于RGBA颜色分量的字节序列。函数fillDataArray()执行此操作，应用黄色和蓝色的RGB值，依据由generate3Dpattern()函数构建并保存在tex3Dpattern数组中的条带图案。另请注意display()函数中指定了纹理类型GL_TEXTURE_3D。

由于我们希望将对象的顶点位置用作纹理坐标，我们将它们从顶点着色器传递到片段着色器。片段着色器缩放它们，以便它们按照纹理坐标的标准，被映射到范围[0, 1]。最后，通过sampler3D统一变量 访问3D纹理，该统一变量采用3个参数而不是两个参数。我们使用顶点的原始X、Y和Z坐标，缩放到正确的范围，以访问纹理。结果如图14.9所示（见彩插）。

图14.9 3D条纹纹理的龙对象

通过修改generate3Dpattern()可以生成更复杂的图案。图14.10显示了将条带图案转换为3D棋盘的简单更改，产生的效果如图14.11所示。值得注意的是，如果龙的表面采用2D棋盘纹理图案进行纹理处理，效果与情况则大不相同。

图14.10 生成棋盘3D纹理图案

图14.11 3D棋盘纹理的龙

14.5 噪声

可以使用随机性或噪声来模拟许多自然现象。一种常见的技术是 Perlin噪声[PE85]，它以Ken Perlin命名。Ken Perlin在1997年因开发生成和使用2D和3D噪声的实用方法而获得奥斯卡奖。[1]这里描述的程序基于Perlin的方法。

图形场景中存在许多噪声应用。一些常见的例子是云、地形、木纹、矿产（如大理石中的矿脉）、烟雾、燃烧、火焰、行星表面和随机运动。在本节中，我们将重点关注生成包含噪声的3D纹理，然后使 用噪声数据生成复杂材质（如大理石和木材），并模拟动画云纹理以用于立方体贴图或天幕。包含噪声的空间数据（例如2D或3D）的集合有时被称为噪声图。

我们首先从随机数据中构建3D纹理贴图。这可以使用上一节中显 示的函数完成，只需进行一些修改。首先，我们使用以下更简单的generateNoise()函数替换程序14.4中的generate3Dpattern()函数：

接下来，修改程序14.4中的fillDataArray()函数，以便将噪声数据复制到字节数组中，以便加载到纹理对象中，如下所示。

程序14.4的其余部分，用于将数据加载到纹理对象并将其应用于模型，依然保持不变。我们可以通过将它应用于我们的简单立方体模型来查看这个3D噪声图，如图14.12所示。在此示例中，noiseHeight= noiseWidth = noiseDepth = 256。

图14.12 3D噪声数据纹理的立方体

这是一个3D噪声图，虽然它不是非常有用（因为它太嘈杂了，很难有很多实际应用）。为了制作更实用、更可调的噪声模式，我们将使用不同的噪声生成过程替换fillDataArray()函数。

假设我们使用整数除法作为索引，通过“放大”，填充数据数组 到图14.12所示的噪声图的一小部分。对fillDataArray()函数的修改如下所示。根据用于除法索引的“缩放”因子，可以使得到的3D纹理 更多或少地呈现“块状”。在图14.13中，纹理显示了放大的结果，将索引分别除以缩放因子8、16和32（从左到右）。

图14.13 不同“缩放”因子的“块状”3D噪声图

通过从每个离散灰度颜色值插值到下一个灰度颜色值，我们可以平滑特定的噪声图内的“块效应”。也就是说，对于给定3D纹理内的每个小“块”，我们通过从其颜色到其相邻块的颜色进行插值来设置块内的每个纹素的颜色。插值代码在下面所示的函数smoothNoise()中，还有修改后的fillDataArray()函数。图14.14所示的是得到的“平滑”纹理（分别是缩放因子2、4、8、16、32和64——从左到右，从上到下）。请注意，缩放因子现在是一个double类型量，因为我们需要小数分量来确定每个纹素的插值灰度值。

图14.14 在各种缩放级别平滑3D纹理

smoothNoise()函数通过计算相应原始“块状”噪声图中纹素周围的8个灰度值的加权平均值来计算给定噪声图的平滑版本中的每个纹素的灰度值。也就是说，它平均纹素所在的小“块”的8个顶点处的颜色值。这些“邻居”颜色中的每一个的权重基于纹素与其每个邻居的距离，并归一化到范围[0…1]。

接下来，组合各种缩放因子的平滑噪声图。创建一个新的噪 图，其中每个纹素由另一个加权平均值形成，这次基于每个“平滑”噪声图中相同位置的纹素的总和，其中缩放因子用作权重。这种效应被Perlin [PE85]称为“湍流”，尽管它与通过求和各种波形产生的谐波实际上更为密切相关。新的turbulence()函数和fillDataArray()的修改版本指定了一个噪声图，该图对缩放级别1～32（2的各次幂）进行求和，如下所示。其中还显示了以此产生的噪声图在立方体上贴图 的结果。

3D噪声图（如图14.15所示）可用于各种富有想象力的应用。在接下来的部分中，我们将使用它们来生成大理石、木材和云。可以通过放大级别的不同组合来调整噪声的分布。

图14.15 “湍流”噪声的3D纹理贴图

14.6 噪声应用——大理石

通过修改噪声图并使用适当的ADS材料添加Phong照明，我们可以使龙模型看起来像一块大理石般的石头，如图7.3所示。

我们首先生成一个条纹图案，有点类似于本章前面的“条纹”示例——新条纹与之前的条纹不同，首先是因为它们是对角线，还因为它们是由正弦波产生的，因此边缘是模糊的。然后，我们使用噪声图 来扰动这些线，将它们存储为灰度值。fillDataArray()函数的更改如下：

变量veinFrequency用于调整条纹数量，turbSize调整生成湍流时 使用的缩放系数，turbPower调整条纹中的扰动量（将其设置为0，使条纹不受干扰）。由于相同的正弦波值用于所有3个（RGB）颜色分量，所以存储在图像数据阵列中的最终颜色是灰度级的。图14.16显示了各种turbPower值（0.0、5.5、1.0和1.5，从左到右）的结果纹理贴图。

图14.16 构建3D“大理石”噪声图

由于我们希望大理石具有闪亮的外观，我们采用Phong着色使得“大理石”纹理物体看起来令人信服。程序14.5总结了生成大理石龙的代码。除了我们还传递了原始顶点坐标以用作3D纹理坐标（如前所述），顶点和片段着色器与用于Phong着色的相同。片段着色器使用前 面7.6节中描述的技术将噪声结果与光照结果结合。

程序14.5 构建大理石龙

有多种方法可以模拟不同颜色的大理石（或其他石材）。改变大理石中“矿脉”颜色的一种方法是修改fillDataArray()函数中Color 变量的定义，例如，通过增加绿色成分：

float redPortion = 255.0f * (float)sineValue;
float greenPortion = 255.0f * (float)min(sineValue*1.5 - 0.25,
1.0);
float bluePortion = 255.0f * (float)sineValue;

我们还可以引入ADS材料值［即在init()中指定］来模拟完全不同类型的石头，例如“玉石”。

图14.17（见彩插）显示了4个示例，前3个使用程序14.5所示的设置，第四个示例包含前面图7.3所示的“jade”ADS材料值。

图14.17 3D噪声图纹理的龙——3个大理石和1个玉质

创建“木材”纹理可以采用与之前“大理石”示例中类似的方式。树木按照年轮生长，正是这些年轮成了我们在用木头制成的物体中看到的“木纹”。随着树木的生长，环境压力会在年轮中产生变化，我们也会在木纹中看到这种变化。

我们首先构建一个程序性的“年轮”3D纹理贴图，类似于本章前面的“棋盘格”。然后，我们使用噪声图来扰动这些年轮，将深色和浅棕色插入年轮纹理贴图中。通过调整年轮的数量以及扰动年轮的程 度，我们可以用各种类型的木纹模拟木材。棕色的色调可以通过组合相似数量的红色和绿色、少量蓝色来制作。然后，我们应用具有低 “光泽”的Phong着色。

我们可以通过修改fillDataArray()函数来生成环绕我们3D纹理贴图中Z轴的年轮，使用三角函数指定与Z轴等距的X和Y值。我们使用正弦波循环重复此过程，根据此正弦波均匀地升高和降低红色和绿色成分，以产生不同的棕色调。变量sineValue保持精确的色调，可以通过稍微偏移一个分量或另一个分量来调整（在这种情况下，将红色增加80，将绿色增加30）。我们可以通过调整xyPeriod的值来创建更多（或更少）的年轮。得到的纹理如图14.18所示（见彩插）。

图14.18 为3D木材纹理创建年轮

图14.18中的木质年轮环是一个很好的开始，但它们看起来不太逼真——它们太完美了。为了改善这一点，我们使用噪声图（更具体地说，是湍流）来扰动distanceFromZ变量，使得环具有轻微的变化。计算修改如下：

同样，变量turbPower调整应用了多少湍流（将其设置为0.0，产生图14.18所示的未受干扰的版本），并且maxZoom指定缩放值（在此 示例中为32）。图14.19显示了turbPower值0.05、1.0和2.0（从左到 右）得到的木材纹理。

图14.19 “木材”3D纹理贴图与噪声地图扰动的年轮

我们现在可以将3D木材纹理贴图应用于模型。通过对用于纹理坐标的originalPosition顶点位置应用旋转，可以进一步增强纹理的真实感，这是因为用木头雕刻的大多数物品与年轮的方向不完全对齐。 为此，我们向着色器发送一个额外的旋转矩阵，以旋转纹理坐标。我们还添加了Phong着色，具有适当的木色ADS值和适度的光泽度。创建 “木质海豚”的完整代码补充和更改见程序14.6。

程序14.6 构建木质海豚

3D材质的木质海豚如图14.20所示。

图14.20 “木材”3D噪声图纹理的海豚

片段着色器中还有一个值得注意的细节。由于我们在3D纹理内旋转模型，所以有时可能会导致顶点位置因旋转而移动超出所需的[0… 1]纹理坐标范围。如果发生这种情况，我们可以通过将原始顶点位置除以更大的数字（例如4.0而不是2.0）来调整这种可能性，然后添加稍大一些的数字（例如0.6）以使其在纹理空间中居中。

14.8 噪声应用——云

前面图14.15中构建的“湍流”噪声图看起来有点像云。当然，它不是正确的颜色，所以我们首先将它从灰度变为适当的浅蓝色和白色混合。一种直接的方法是为蓝色分量指定一个最大值为1.0的颜色，为红色和绿色分量指定0.0～1.0的变化（但相等的）值，具体取决于噪声图中的值。新的fillDataArray()函数如下：

生成的蓝色版本的噪声图现在可用于纹理化天幕。回想一下，天幕是一个球体或半球体，在禁用深度测试的情况下被纹理化和渲染，并放置使其围绕相机（类似于天空盒）。

构建天幕的一种方法是使用顶点坐标作为纹理坐标，以与我们对其他3D纹理相同的方式对其进行纹理化。然而，在这种情况下，事实证明使用天幕的2D纹理坐标会产生看起来更像云的图案，因为球面扭曲会略微拉伸纹理贴图。我们可以通过将GLSL的texture()调用中的第三维设置为常量值来从噪声图中获取2D切片。假设天幕的纹理坐标已经以标准方式发送到顶点属性中的OpenGL管线，下面的片段着色器使用噪声图的2D切片对其进行纹理化：

得到的纹理化天幕如图14.21所示（见彩插）。虽然相机通常被放 置在天幕内，但我们在外面使用相机进行渲染，因此可以看到圆顶本 身的效果。当前的噪声图导致云“看起来模糊不清”。

图14.21 云雾缭绕纹理的天幕

虽然我们的朦胧云看起来不错，但我们希望能够塑造它们——也就是说，让它们更多或更少朦胧。一种方法是修改turbulence()函数，使其使用指数（如logistic函数），[2]让云看起来更“明显”。 修改后的turbulence()函数以及相关的logistic()函数如程序14.7所 示。完整的程序14.7还包含前面描述的smooth()、fillDataArray()和 generateNoise()函数。

程序14.7 云纹理生成

Logistic函数使颜色更倾向于白色或蓝色，而不是介于两者之间的值，从而产生具有更多不同云边界的视觉效果。变量cloudQuant调整噪声图中白色（相对于蓝色）的相对量，这反过来导致当应用 logistic函数时产生更多（或更少）的白色区域（即不同的云）。由 此产生的天幕现在具有更明显的云层，如图14.22所示（见彩插）。

图14.22 指数云纹理的天幕

最后，真正的云不是静态的。为了增强云的真实感，我们应该通过以下方式使它们变得生动：

1. 使它们随着时间的推移而移动或 “漂移”；
2. 随着它们漂移逐渐改变它们的形状。

使云“漂移”的一种简单方法是缓慢旋转天幕。这不是一个完美的解决方案，因为真实的云往往会沿着直线方向漂移，而不是围绕观察者旋转。但是，如果旋转缓慢且云只是用于装饰场景，则效果可能是足够的。

随着云的漂移，云逐渐变化，起初可能看起来很棘手。然而，考虑到我们用于纹理云的3D噪声图，实际上有一种非常简单而聪明的方法来实现这种效果。回想一下，虽然我们为云构建了一个3D纹理噪声图，但到目前为止我们只使用了它的一个“切片”，跟天幕的2D纹理坐标相交（我们将纹理查找的Z坐标设置为一个常量值）。到目前为
止，3D纹理的其余部分尚未使用。

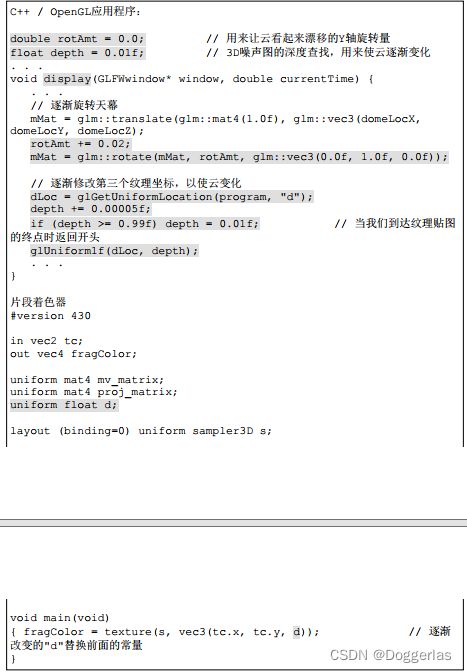
我们的技巧是将纹理查找的常量Z坐标替换为随时间逐渐变化的变量。也就是说，当我们旋转天幕时，我们逐渐增加深度变量，导致纹理查找使用不同的切片。回想一下，当我们构建3D纹理贴图时，我们将平滑应用于沿3个轴的颜色变化。因此，纹理贴图中的相邻切片非常相似，但略有不同。因此，通过逐渐改变texture()调用中的Z值，云的外观将逐渐改变。 代码更改导致云缓慢移动并随时间变化，如程序14.8所示。
程序14.8 动画云纹理

虽然我们无法在单个静止图像中显示逐渐改变漂移和动画的云的 效果，但图14.23显示了3D生成云的一系列快照中的这些变化，因为它们从右到左漂移在天幕上，并在漂移时缓慢改变形状。

图14.23 3D云在漂移时改变

14.9 噪声应用——特殊效果

噪声纹理可用于各种特殊效果。事实上，有许多可能的用途，其适用性仅受到想象力的限制。

我们将在此展示的一个非常简单的特殊效应是溶解效应。我们使物体看起来逐渐溶解成小颗粒，直到它最终消失。给定3D噪声纹理， 可以使用非常少的附加代码实现此效果。

为了促进溶解效果，我们引入了GLSL的discard命令。此命令仅在片段着色器中是合法的，并且在执行时，它会导致片段着色器丢弃当前片段（意味着不渲染它）。

我们的策略很简单。在C++/OpenGL应用程序中，我们创建了一个与图14.12所示相同的细粒度噪声纹理贴图，以及随时间逐渐增加的浮点变量计数器。然后，此变量在着色器管线中以统一变量发送，并且噪声图也放置在具有关联采样器的纹理贴图中。然后片段着色器使用采样器访问噪声纹理——在这种情况下，我们使用返回的噪声值来确 定是否丢弃该片段。我们通过将灰度噪声值与计数器进行比较来实现这一点，计数器用作一种“阈值”值。因为阈值随着时间的推移逐渐变化，我们可以将其设置为逐渐丢弃越来越多的片段。结果是物体似乎逐渐溶解。程序14.9显示了相关的代码部分，它们被添加到程序6.1中的地球渲染球体中。生成的输出如图14.24所示。

程序14.9 使用discard命令的溶解效果

图14.24 使用discard着色器的溶解效果

如果可能，丢弃命令应该谨慎使用，因为它可能会导致性能损失。这是因为它的存在使OpenGL更难以优化Z缓冲深度测试。

补充说明

在本章中，我们使用Perlin噪声生成云、模拟木材和大理石般的石头，并且用它们渲染龙。人们发现了Perlin噪音的许多其他用途。 例如，它可用于创建火焰和烟雾[CC16，AF14]，构建逼真的凹凸贴图[GR05]，并已在电子游戏Minecraft [PE11]中用于生成地形。

本章生成的噪声图基于Lode Vandevenne [VA04]描述的程序。我们的3D云生成仍存在一些不足之处。纹理不是无缝的，所以在360°点有一条明显的垂直线（这也是我们在程序14.8中以0.01而不是0.0开始深度变量的原因，以避免在噪声图的Z维中遇到接缝）。如果需要，也有用于去除接缝[AS04]的简单方法。另一个问题是在天幕的北峰处，天幕中的球形畸变会产生枕形效应。

我们在本章中实现的云也无法模拟真实云的一些重要方面，例如它们散射太阳光的方式。真正的云也往往在顶部更白，在底部更灰暗。我们的云也没有达到许多实际云所具有的3D“蓬松”外观。

类似地，存在用于产生雾的更全面的模型，例如Kilgard和 Fernando [KF03]描述的模型。

在阅读OpenGL文档时，读者可能会注意到GLSL包含一些名为 noise1()、noise2()、noise3()和noise4()的噪声函数，它们被描述为采用输入种子并产生类似高斯的随机输出。我们在本章中没有使用这些函数，因为在撰写本文时，大多数供应商都没有实现它们。例如，无论输入种子如何，许多NVIDIA显卡目前只会为这些函数返回0值。