幻方加密代码——自动生成幻方密钥方法，罗伯法单偶数阶的解法代码基于python

前导：

罗伯法的口诀：

1、奇数阶幻方

2、双偶阶幻方

3、单偶阶幻方

自动生成幻方密钥：

---

前导：

        幻方加密是基于罗伯法的填数自动生成阶级数阵来作为密钥，要明白幻方加密，首先就要先了解罗伯法的规律，编写代码时幻方加密的情况分为了3种情况，基数阶的填数，单偶与双偶阶，本篇实现幻方加密代码是基于python编写

先了解一下什么是幻方阶

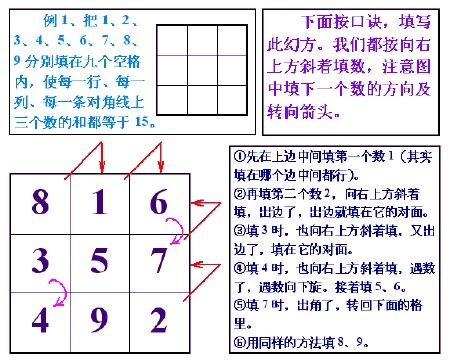
        阶幻方，每一行、每一列、两对角线上的数之和相等。当n为奇数时，我们称幻方为奇阶幻方。法国人罗伯总结出了构造奇数阶连续自然数幻方的简单易行的方法“罗伯法”。图1就是一个用罗伯法排好的5阶幻方

罗伯法的口诀：

（初学者可先画出一个N×N的方格阵）

1 居上行正中央——数字 1 放在首行最中间的格子中

依次斜填切莫忘——向右上角斜行，依次填入数字

上出框界往下写——如果右上方向出了上边界，就以出框后的虚拟方格位置为基准，将数字竖直降落至底行对应的格子中

右出框时左边放——同上，向右出了边界，就以出框后的虚拟方格位置为基准，将数字平移至最左列对应的格子中

重复便在下格填——如果数字{N} 右上的格子已被其它数字占领，就将{N+1} 填写在{N}下面的格子中

右上重复一个样——如果朝右上角出界，和“重复”的情况做同样处理

1、奇数阶幻方

        n为奇数 【n=3，5，7，9，11……】 【n=2×k+1，k=1，2，3，4，5……)】
奇数阶幻方最经典的填法是罗伯特法【也有人称之为楼梯法】

填写方法是这样：
把1(或最小的数)放在第一行正中； 按以下规律排列剩下的n×n-1个数：

(1)每一个数放在前一个数的右上一格；
(2)如果这个数所要放的格已经超出了顶行那么就把它放在底行，仍然要放在右一列；
(3)如果这个数所要放的格已经超出了最右列那么就把它放在最左列，仍然要放在上一行；
(4)如果这个数所要放的格已经超出了顶行且超出了最右列，那么就把它放在前一个数的下一行同一列的格内；
(5)如果这个数所要放的格已经有数填入，处理方法同(4)。
这种写法总是先向“右上”的方向，象是在爬楼梯。

2、双偶阶幻方

        n为偶数，且能被4整除 【n=4，8，12，16，20…】 【n=4k，k=1，2，3，4，5…】
先说明一个定义。互补：如果两个数字的和，等于幻方最大数和最小数的和，即 n*n+1，称为互补。
        先看看4阶幻方的填法：将数字从左到右、从上到下按顺序填写：

        这个方阵的对角线，已经用颜色标出。将对角线上的数字，换成与它互补（同色）的数字。
这里，n×n+1 = 4×4+1 = 17；把1换成17-1 = 16；把6换成17-6 = 11；把11换成17-11 = 6……换完后就是一个四阶幻方。
        对于n=4k阶幻方，我们先把数字按顺序填写。写好后，按4*4把它划分成k*k个方阵。因为n是4的倍数，一定能用4*4的小方阵分割。然后把每个小方阵的对角线，象制作4阶幻方的方法一样，对角线上的数字换成互补的数字，就构成幻方。
 

3、单偶阶幻方

        n为偶数，且不能被4整除 【n=6，10，14，18，22…】 【n=4k+2，k=1，2，3，4，5…】
这是三种里面最复杂的幻方。
以n=10为例。这时，k=2

(1) 把方阵分为A，B，C，D四个象限，这样每一个象限肯定是奇数阶。用楼梯法，依次在A象限，D象限，B象限，C象限按奇数阶幻方的填法填数。

(2) 在A象限的中间行、中间格开始，按自左向右的方向，标出k格。A象限的其它行则标出最左边的k格。将这些格，和C象限相对位置上的数，互换位置。

(3) 在B象限任一行的中间格，自右向左，标出k-1列。(注：6阶幻方由于k-1=0，所以不用再作B、D象限的数据交换)，将B象限标出的这些数，和D象限相对位置上的数进行交换，就形成幻方。

自动生成幻方密钥：

        复制代码前，先把文件创建好，把代码的路径设置好，如果只需要输出幻方，可以把文件部分直接改成输出即可。

import numpy as np

#列表循环向左移offset位
def shift_left(lst, offset):
    return [lst[(i+offset)%len(lst)] for i in range(len(lst))]

#列表循环向右移offset位
def shift_right(lst, offset):
    return [lst[i-offset] for i in range(len(lst))]

#构造奇数阶幻方函数
def magic_of_odd_order(n):
    p = (int)((n-1)/2)

    #创建矩阵1
    initial_lst1 = list(range(p+1,n))+list(range(p+1))
    initial_mat1 = []
    for i in range(n):
        initial_mat1.append(shift_left(initial_lst1, i))
    mat1 = np.array(initial_mat1)

    #创建矩阵2
    initial_lst2 = list(range(p,-1,-1))+list(range(2*p,p,-1))
    initial_mat2 = []
    for i in range(n):
        initial_mat2.append(shift_right(initial_lst2, i))
    mat2 = np.array(initial_mat2)

    #创建矩阵3,即元素全为1的矩阵
    mat3= np.ones((n,n),dtype=np.int_)

    #构造幻方
    magic = n*mat2+mat1+mat3
    return magic

#构造4n阶幻方函数
def magic_of_4n_order(n):
    mat = np.array(range(1,n*n+1)).reshape(n,n)
    for i in range((int)(n/4)):
        for j in range((int)(n/4)):
            for k in range(4): #将每个4*4小方块的对角线换成互补元素
                mat[k+4*j][k+4*i] = n*n+1-mat[k+4*j][k+4*i]
                mat[k+4*j][3-k+4*i] = n*n+1-mat[k+4*j][3-k+4*i]

    return mat

#构造4n+2阶幻方函数
def magic_of_4n2_order(n):
    p = (int)(n/2)
    matA = magic_of_odd_order(p)
    matD = matA+p**2
    matB = matD+p**2
    matC = matB+p**2

    #交换矩阵块A与矩阵块C中特定元素的位置
    row = (int)((p-1)/2)
    for i in range(p):
        if i != row:
            for k in range((int)((n-2)/4)):
                matA[i][k],matC[i][k] = matC[i][k],matA[i][k]
        else:
            for k in range((int)((n-2)/4)):
                matA[i][row+k],matC[i][row+k] = matC[i][row+k],matA[i][row+k]

   
    col = (int)((p-1)/2)
    for j in range(col+2-(int)((n-2)/4),col+1):
        for i in range(p):
            matB[i][j],matD[i][j] = matD[i][j],matB[i][j]

    
    magic = np.row_stack((np.column_stack((matA,matB)),np.column_stack((matC,matD))))
    return magic
n1=[]
def main():
    order = eval(input('输入幻方阶数(>=3): '))

    if order%2 ==1:
        magic = magic_of_odd_order(order)
    elif order%4 == 0:
        magic = magic_of_4n_order(order)
    else:
        magic = magic_of_4n2_order(order)
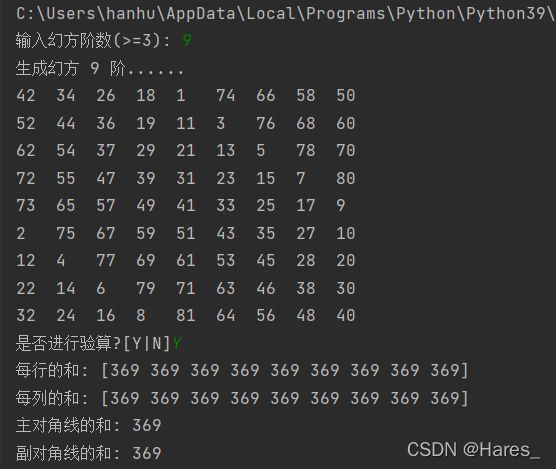
    print('生成幻方 %d 阶......'%order)

    for row in magic:
        for col in row:
            n1.append(col)
            print(col, end='\t')
        print()

    #验证生成的magic是否为幻方 
    val = input(("是否进行验算?[Y|N]"))
    if val == 'Y' or val == 'y':
        print('每行的和:', np.sum(magic, axis=0))
        print('每列的和:', np.sum(magic, axis=1))
        print('主对角线的和:', sum([magic[i][i] for i in range(order)]))
        print('副对角线的和:', sum([magic[i][order-1-i] for i in range(order)]))
    
main()

f = open(r"C:\Users\hanhu\Desktop\加密解密\明文.txt", "r")
a=f.read().split()
f.close()
#a=str(a)
#a=input().split()
b=list(map(int,n1))
k=dict.fromkeys(b,' ')
for i in range(len(n1)-len(a)):
    a.append(' ')
for i in range(len(k)):
    k[b[i]]=a[i]
l=""
for i in range(len(k)):
    l+=k[i+1]+' '
l=l[:-1]
f = open(r"C:\Users\hanhu\Desktop\加密解密\幻方密文.txt", "w")
f.write(l)
f.close()

 

执行：