java中方法的使用和递归(三个维度讲递归)+递归练习【详解篇5】
文章目录
-
- 方法
-
- 什么是方法?
- 方法定义的语法
- 方法调用的执行过程
- 实参和形参的关系
- 没有返回值的方法
- 方法的重载
-
- 重载的规则
- 递归
-
- 从第一个维度来看递归:当n=3时
- 从第二个维度来看递归:当n=4时
- 从第三个维度来看递归:当n=4时:
- 递归练习题
-
- 练习1:递归求 N 的阶乘
- 练习2:按顺序打印一个数字的每一位
- 练习3:递归求 1 + 2 + 3 + ... + 10
- 练习4:写一个递归方法,输入一个非负整数,返回组成它的数字之和.
- 练习5:求斐波那契数列的第N项
- 练习6:青蛙跳台阶问题
- 练习7:汉诺塔问题
方法
什么是方法?
方法就是一个代码片段. 类似于 C 语言中的 “函数”.
把一些重复的功能抽象出来当用的上它的时候就把它拿过来用,在这里我们叫调用。
方法存在的意义:
1.是能够模块化的组织代码(当代码规模比较复杂的时候)。
2.做到代码被重复使用, 一份代码可以在多个位置使用。
3.让代码更好理解更简单。
4.直接调用现有方法开发, 不必重复造轮子。
代码示例1:计算1!+2!+3!+4!+5!
public class Method1 {
public static void main(String[] args) {
int sum=0;
int i=0;
for(i=1;i<=5;i++){
int tmp=1;
for(int j=1;j<=i;j++){
tmp*=j;
}
sum=sum+tmp;
}
System.out.println("sum="+sum);//运行结果:153
}上面这个代码中使用双重循环, 比较容易写错.接下来我们可以使用方法来优化这个代码,通过这个代码先让我们对方法有一个初步的认识。
代码示例2:使用方法,计算1!+2!+3!+4!+5!
public static int facSum(int n){
int sum=0;
for(int i=1;i<=n;i++){//求n的阶乘的和
sum+=fac(i);
}
return sum;//3.返回值只能返回一个数据;4.return 的后面不能再写任何代码了,因为编译器认为return代表函数的结束
}
public static int fac(int n){
int ret=1;
for(int i=1;i<=n;i++){//求n的阶乘
ret*=i;
}
return ret;
}
public static void main(String[] args) {
int ret=facSum(5);//1.返回值类型要匹配;2.参数的个数和参数的类型都要匹配
System.out.println(ret);//运行结果:153
}注意:
1.返回值类型要匹配;
2.参数的个数和参数的类型都要匹配
3.返回值只能返回一个数据;
4.return 的后面不能再写任何代码了,因为编译器认为return代表函数的结束
方法定义的语法
基本语法
//方法定义
public static 方法返回值 方法名称([参数类型 形参 ...]){形式参数列表可以是多个参数
方法体代码;
[return 返回值];
}
//方法调用
返回值变量 = 方法名称(实参...);代码示例3:实现一个方法实现两个整数相加
public static void main(String[] args) {
int a=20;
int b=1;
//方法的调用
int sum=add1(a,b);//实参
System.out.println("sum="+sum);//运行结果:21
}
//方法的定义
public static int add1(int x,int y){//形参
return x+y;
}注意:
- public 和 static 两个关键字在此处具有特定含义, 在这里呢我们先暂时不讨论, 学到后面再详细介绍.
- 方法定义时, 参数可以没有,但如果有参数每个参数要指定类型
- 方法定义时, 返回值也可以没有, 如果没有返回值, 则返回值类型应写成 void
- 方法定义时的参数称为 “形参”, 方法调用时的参数称为 “实参”.
- 方法的定义必须在类之中, 代码书写在调用位置的上方或者下方均可.
- Java 中没有 “函数声明” 这样的概念,和C不一样,并没有什么函数在使用前要声明的要求
方法调用的执行过程
基本规则:
1.定义方法的时候, 不会执行方法的代码. 只有调用的时候才会执行.
2.当方法被调用的时候, 会将实参赋值给形参.
3.参数传递完毕后, 就会执行到方法体代码.
4.当方法执行完毕之后(遇到 return 语句), 就执行完毕, 回到方法调用位置继续往下执行.
5.一个方法可以被多次调用,如示例4。
代码示例4:计算两个整数相加。
public static void main3(String[] args) {
int a=99;
int b=1;
System.out.println("第一次调用方法之前");
int sum=add2(a,b);
System.out.println("第一次调用方法之后");
System.out.println("sum="+sum);
System.out.println("第二次调用方法之前");
sum=add2(30,50);
System.out.println("第二次调用方法之后");
System.out.println("sum="+sum);
}
public static int add2(int x,int y){
System.out.println("调用方法中 x="+x+" "+"y="+y);
return x+y;
}打印结果如下:
代码示例5:使用方法计算1!+2!+3!+4!+5!
public static void main(String[] args) {
int sum=0;
for(int i=1;i<=5;i++){//计算n的阶乘的和
sum+=fuc(i);
}
System.out.println("sum="+sum);
}
public static int fuc(int n){//计算n的阶乘
System.out.println("计算 n 的阶乘中! n = " + n);
int tmp=1;
for(int j=1;j<=n;j++){
tmp*=j;
}
return tmp;
}打印结果:验证基本规则
实参和形参的关系
在了解实参和形参的关系之前我们先来了解一下函数调用的原理。
一个函数要想被调用那么它有哪些原理呢?
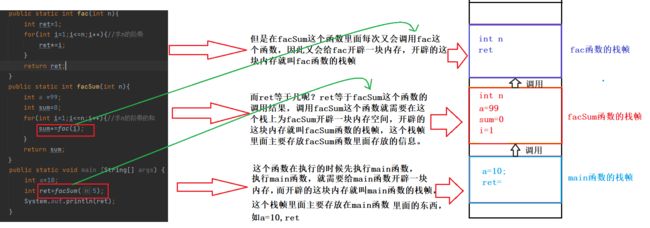
首先,所有的函数在执行的时候,都是需要在栈上开辟内存的,而这个内存就是指栈帧。
下图就是函数开辟栈帧的过程及函数调用的原理。
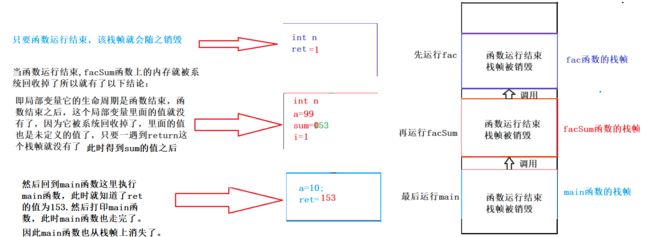
函数运行结束,函数栈帧消失的过程如下:
以上就是函数调用的原理,总结成一句话就是:函数的调用需要在栈上开辟栈帧,当函数调用结束之后,该栈帧就会被系统回收,栈帧里面的值就会被销毁了。
明白了函数调用的原理,就明白了为什么局部变量的作用域是在函数体内了。
也可以明白下面这个代码中两个变量a,b 的值是不一样的,因为他们在不同的栈帧,因此代表着不同的意义。
public static void func(int a,int b){
}
public static void main(String[] args) {
int a=10;
int b=20;
}
}代码示例6:交换两个整型变量
public static void main(String[] args) {
int a=10;
int b=20;
//交换之前打印
System.out.println("a="+a+","+"b="+b);//a=10,b=20
swap(a,b);
System.out.println("============================");
//交换之前打印
System.out.println("a="+a+","+"b="+b);//a=10,b=20
}
public static void swap(int a,int b){
int tmp=a;
a=b;
b=tmp;
}运行结果是:a=10,b=20,但其实我们想要的运行结果是a=20,b=10,为什么没有达到我们想要的结果呢?
原因分析:刚才的代码,没有完成数据的交换,只交换了形参,没有交换实参。
对于基础类型来说,形参相当于实参的拷贝,即传值调用,不同于C语言中的传址调用。
那如何把地址传过去呢?即传址调用
1.在java里面是没有指针的
2.在java里面是拿不到栈上变量的地址的,也就是说在栈上的地址是拿不到的,在java里面是没有所谓的取地址这一说的
代码示例7如下: 对 x 和 y 的修改, 不影响 a 和 b.
public static void main6(String[] args) {
int a=99;
int b=1;
int x=a;
int y=b;
int tmp=x;
x=y;
y=tmp;
System.out.println("a="+a+","+"b="+b);
System.out.println("x="+x+","+"y="+y);
}解决办法: 传引用类型参数 (例如数组来解决这个问题),这个代码的运行过程, 后面学习数组的时候再详细解释。
代码示例8:解决上述没有完成数据的交换的问题
public static void main7(String[] args) {
int[] arr={10,20};
System.out.println("交换前:"+"a="+arr[0]+","+"b="+arr[1]);
swap1(arr);
System.out.println("交换后:"+"a="+arr[0]+","+"b="+arr[1]);
}
public static void swap1(int[] arr){
int tmp=arr[0];
arr[0]=arr[1];
arr[1]=tmp;
}没有返回值的方法
方法的返回值是可选的,有些时候是可以没有的,如果没有返回值, 则返回值类型应写成 void。
代码示例9:如果没有返回值, 则返回值类型应写成 void
public static void main8(String[] args) {
int a=999;
int b=888;
print(a,b);
}
public static void print(int x,int y){
System.out.println("x="+x+","+"y="+y);
}方法的重载
有些时候我们需要用一个函数同时兼容多种参数的情况,就可以使用方法的重载。
重载要解决的问题
代码示例10:重载错误演示
public static void main9(String[] args) {
int a=20;
int b=10;
int ret=add(a,b);
System.out.println("ret="+ret);
double a1=11.5;
double b1=12.5;
// double ret1=add(a1,b1);// 报错
//System.out.println("retq="+ret1);
}
public static int add(int x,int y){
return x+y;
}运行结果:D:\java代码\2021-07-29\src\TestDemo1.java:161:23
java: 不兼容的类型: 从double转换到int可能会有损失:161行
错误原因:由于参数类型不匹配, 所以不能直接使用现有的 add 方法.
解决方法:代码示例11
public static void main10(String[] args) {
int a=20;
int b=10;
int ret=addInt(a,b);
System.out.println("ret="+ret);
double a1=11.5;
double b1=12.5;
double ret1=addDouble(a1,b1);
System.out.println("retq="+ret1);
}
public static int addInt(int x,int y) {
return x + y;
}
public static double addDouble(double x,double y){
return x+y;
}这样的写法是对的(例如 Go 语言就是这么做的), 但是 Java 认为 addInt 这样的名字不友好, 不如直接就叫 add,java支持方法(函数)名一样。
代码示例12:方法名一样的例子
public static void main(String[] args) {
int a1 = 10;
int b1 = 20;
int ret1 = adds(a1, b1);
System.out.println("ret1 = " + ret1);
double a2 = 10.5;
double b2 = 20.5;
double ret2 = adds(a2, b2);
System.out.println("ret2 = " + ret2);
float a3 = 10.5f;
float b3 = 10.5f;
float c3 = 20.5f;
float ret3 = adds(a3, b3, c3);
System.out.println("ret3 = " + ret3);
}
public static int adds(int x, int y) {
return x + y;
}
public static double adds(double x, double y) {
return x + y;
}
public static float adds(float x, float y, float z) {
return x + y + z;
}运行结果:
方法的名字都叫 adds. 但是有的 adds 是计算 int 相加, 有的是 double 相加;有的是 float 相加; 有的计算两个数字相加, 有的是计算三个数字相加。
总结:同一个方法名字, 提供不同版本的实现, 称为方法重载
重载的规则
- 针对同一个类:
1.方法名相同
2.方法的参数不同(参数个数或者参数类型)
3.方法的返回值类型不影响重载
4.重载不是必须要在一个类当中 - 什么是方法的重写?学了继承才知道,以后再说。
递归
递归的概念:一个方法在执行过程中调用自身(即自己调用自己), 就称为 “递归”.它有一个趋近于终止的条件。
- 递归相当于数学上的 “数学归纳法”, 有一个起始条件, 然后有一个递推公式,因此想要学好递归就需要大量的练习和思考!
- 递归是横向思考,纵向执行,每一个代码都有一个递推公式,写代码的核心就是找出递推公式,找到公式代码就会好些很多。
下面我们先根据这个代码从三个维度来看看递归是怎么做的,它的执行过程是怎样的?原理是什么?
public static void main1(String[] args) {
Scanner s = new Scanner(System.in);
int num = s.nextInt();
int ret = factor(num);
System.out.println("ret=" + ret);
}
public static int factor(int n) {
if (n == 1) {
return 1;
}
int ret = n * factor(n - 1);//factor调用函数自身
return ret;
}从第一个维度来看递归:当n=3时
递归的程序的执行过程不太容易理解, 要想理解清楚递归, 必须先理解清楚 “方法的执行过程”, 尤其是 "方法执行结束之后,回到调用位置继续往下执行。
总结:
(1)代码在往下递归的时候,并不是一下子就得出最终结果的,而是经过一次一次的函数计算并递归下去才知道了返回值是几,从而才能得到它的返回值。
(2)纵向执行代码意思就是将代码展开,如上面画的图,但它不适用于计算较大的数;因此我们需要横向思考,通过推导出递推公式,来将大问题转化成小问题,这样写代码才会容易的多。
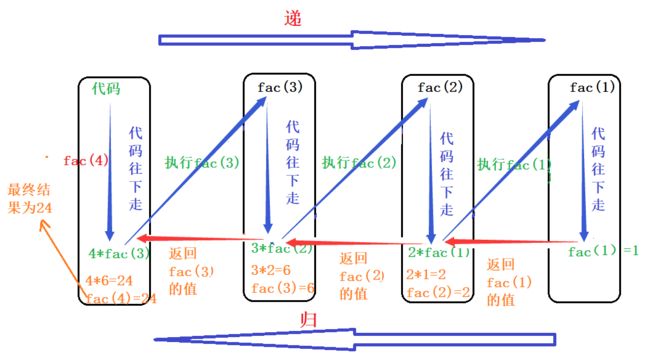
从第二个维度来看递归:当n=4时
总结:
(1)递归,可以把它看成是递和归两个过程,因为递和归都属于动词,所以上面是递的过程,下面是归的过程,以什么样的方式递过去,就以什么样的方式归回来;
(2)上图可以看出递归的过程,即在往下递的时候,
执行fac(4)时,它需要等fac(3)执行完,
执行fac(3)时,它需要等fac(2)执行完,
执行fac(2)时,它需要等fac(1)执行完,
fac(1)执行完得fac(1)=1然后开始返回,fac(1)的值返回计算出fac(2)的值,
然后返回fac(2)的值计算出fac(3)的值,
然后返回fac(3)的值计算出fac(4)的值,直到函数全部执行完毕,得出最终结果。
以上就是从第二个维度上来理解递归。
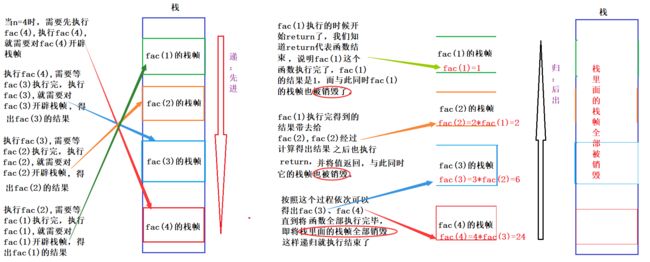
从第三个维度来看递归:当n=4时:
我们知道递归是发生在栈上的,栈的特点是先进后出,而函数调用是需要栈来开辟栈帧的。
- 关于 “调用栈”
方法调用的时候, 会有一个 “栈” 这样的内存空间描述当前的调用关系. 称为调用栈.
每一次的方法调用就称为一个 “栈帧”, 每个栈帧中包含了这次调用的参数是哪些, 返回到哪里继续执行等信息,具体过程如下图所示.
总结:这里的递归过程就是以先递下去再归回来,在递下去归回来时是以原路归回的,也就相当于函数在栈上开辟内存一样,最后一次执行完,依次开始回退。
以上三个维度就是对递归的理解以及它的原理。
递归练习题
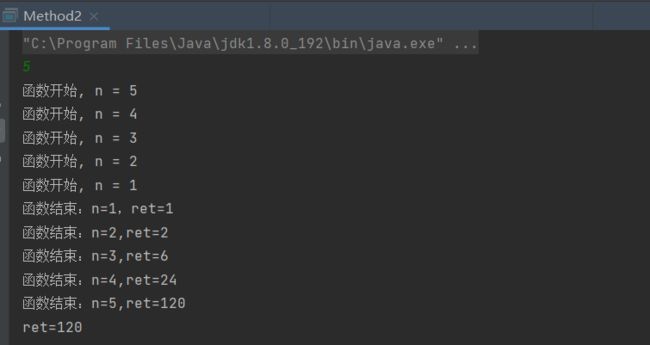
练习1:递归求 N 的阶乘
public static void main1(String[] args) {
Scanner s = new Scanner(System.in);
int num = s.nextInt();
int ret = factor(num);
System.out.println("ret=" + ret);
}
public static int factor(int n) {
System.out.println("函数开始, n = " + n);
if (n == 1) {
System.out.println("函数结束:n=1,ret=1");
return 1;
}
int ret = n * factor(n - 1);//factor调用函数自身
System.out.println("函数结束:n=" + n + "," + "ret=" + ret);
return ret;
}
打印结果:
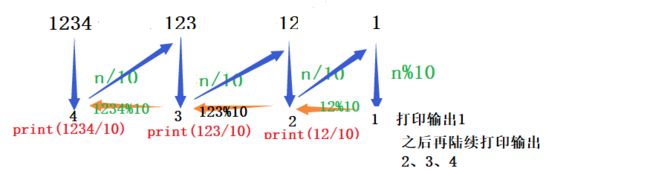
练习2:按顺序打印一个数字的每一位
(例如 1234 打印出 1 2 3 4)。
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int num = scanner.nextInt();
print(num);
}
public static void print(int n) {
if (n > 9) {
print(n / 10);
}
System.out.print(n % 10 + " ");
}打印结果:
画图理解:
练习3:递归求 1 + 2 + 3 + … + 10
分析后得递推公式为:1+sum(n-1)的和
public static void main3(String[] args) {
int num = 10;
System.out.println(sum(num));
}
public static int sum(int num) {
if (num == 1) {
return 1;
}
return num + sum(num - 1);
}打印结果:
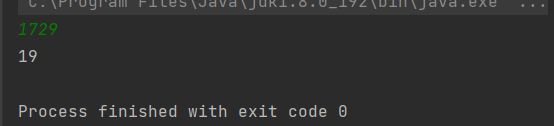
练习4:写一个递归方法,输入一个非负整数,返回组成它的数字之和.
例如,输入 1729, 则应该返回1+7+2+9,它的和是19。
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int num1 = scanner.nextInt();
System.out.println(sum1(num1));
}
public static int sum1(int num1) {
if (num1 < 10) {
return num1;
}
return num1 % 10 + sum1(num1 / 10);
}
//也可写成大于
public static int sum1(int num1) {
if (num1 > 10) {
return sum1(num1 / 10)+num1 % 10;
}
return num1 % 10 ;
}打印结果:
练习5:求斐波那契数列的第N项
介绍斐波那契数列:斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家莱昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,
故又称为“兔子数列”,指的是这样一个数列:0、1、1、2、3、5、8、13、21、34、……
在数学上,斐波那契数列以如下被以递推的方法定义:F(0)=0,F(1)=1, F(n)=F(n - 1)+F(n - 2)(n ≥ 2,n ∈ N*)
在现代物理、准晶体结构、化学等领域,斐波纳契数列都有直接的应用,
为此,美国数学会从 1963 年起出版了以《斐波纳契数列季刊》为名的一份数学杂志,用于专门刊载这方面的研究成果。
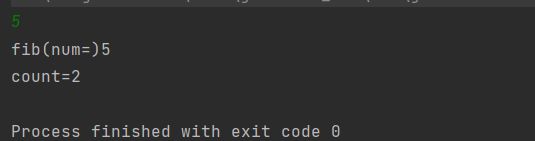
使用递归求斐波那契数列的第N项
public static int count = 0;
public static void main6(String[] args) {
Scanner scanner = new Scanner(System.in);
int num = scanner.nextInt();
System.out.println("fib(num=)" + fib(num));
System.out.println("count=" + count);
}
public static int fib(int n) {
if (n == 1 || n == 2) {
return 1;
}
if (n == 3) {
count++;
}
return fib(n - 1) + fib(n - 2);
}但使用递归求斐波那契数是不好的,因为会有很多重复的计算,因此不建议使用递归求斐波那契数,建议使用迭代(也就是循环)。
使用循环的方式来求斐波那契数列问题, 避免出现冗余运算
public static void main(String[] args) {
Scanner scanner=new Scanner(System.in);
int s=scanner.nextInt();
System.out.println("fib2(s=)"+fib2(s));
}
public static int fib2(int s) {
if(s==1||s==2){
return 1;
}
int num1=1;
int num2=1;
int tmp=0;
for(int i=3;i<=s;i++){
tmp=num1+num2;
num2=num1;
num1=tmp;
}
return tmp;
}
}打印结果:
- 递归是一种重要的编程解决问题的方式.
有些问题天然就是使用递归方式定义的(例如斐波那契数列, 二叉树等), 此时使用递归来解就很容易.
有些问题使用递归和使用非递归(循环)都可以解决. 那么此时更推荐使用循环, 相比于递归, 非递归程序更加高效
练习6:青蛙跳台阶问题
问题描述:一只青蛙一次可以跳上 1 级台阶,也可以跳上2 级。求该青蛙跳上一个n 级的台阶总共有多少种跳法。
public class TestFrog {
public static int jumpFloor(int target){
if(target==1){
return 1;
}
if (target==2){
return 2;
}
return jumpFloor(target-1)+jumpFloor(target-2);
}
public static void main(String[] args) {
Scanner s=new Scanner(System.in);
int target=s.nextByte();
System.out.println(jumpFloor(target));
}
}打印结果:
练习7:汉诺塔问题
问题描述:汉诺塔问题
是一个经典的问题。汉诺塔(Hanoi Tower),又称河内塔,源于印度一个古老传说。
大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。
大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,任何时候,在小圆盘上都不能放大圆盘,且在三根柱子之间一次只能移动一个圆盘。问应该如何操作?
分析:
- 1.只有一个盘子时:将①从A直接挪到C(A->C) 1 2^1-1
- 2.有两个盘子时:将②盘子挪到B,再将①盘子A挪到C,再将②盘子从B挪到C(A->B A->C B->C) 3 2^2-1
- 3.有三个盘子时,将③盘子挪到C,将②盘子挪到B,将③从C挪到B,将①盘子从A挪到C,将③盘子从B挪到A,将②盘子从B挪到C,最后,将①盘子从A挪到C(A->C A->B C->B A->C B->A B->C A->C) 7 2^3-1
- 4.有四个盘子时,…2^4-1
- n.有n个盘子时,n. …2^n-1
public class TestHanoiTower {
public static void move(char pos1,char pos2) {
System.out.print(pos1+"—>"+pos2+" ");
}
/*n:当前盘子的个数
* pos1:起始位置
* pos2:中转位置
* pos3:目的位置*/
public static void hanoiTower(int n,char pos1,char pos2,char pos3){
if(n==1){
move(pos1,pos3);//A->C
}else{
hanoiTower(n-1,pos1,pos3,pos2);//将起始位置在pos1上的盘子通过pos3移到pos2
move(pos1,pos3);//将pos1的盘子移动到pos3上
hanoiTower(n-1,pos2,pos1,pos3);//将起始位置在pos2上的盘子通过pos1移到pos3
}
}
public static void main(String[] args) {
hanoiTower(1,'A','B','C');
System.out.println();
hanoiTower(2,'A','B','C');
System.out.println();
hanoiTower(3,'A','B','C');
System.out.println();
}
}