Task7_KNN(K最近邻分类)算法
KNN(K最近邻分类)算法
如果有一个数据集中,有N类数据。输入没有标分类的数据集后,我们可以将预测集中的数据,和训练集的数据相比较,提取和预测数据最相似(距离最近)的K个数据,选择这K个数据中出现次数最多的标签,作为新数据的分类。
KNN算法的思想非常简洁直观:
1、计算测试数据与各个训练数据之间的距离;
2、按照距离的递增关系进行排序;
3、选取距离最小的K个点;
4、确定前K个点所在类别的出现频率;
5、返回前K个点中出现频率最高的类别作为测试数据的预测分类。
KNN算法的优点:
1、简单,易于实现;
2、因为找的是最近邻的数据点,因此当某些点数量稀少时,划分越准确,适合对稀有点分类;
3、使用多分类问题。
算法实现
我们利用一个案例,按照KNN算法的思想,逐步实现算法。
KNN案例:优化约会网站的配对效果
项目概述
海伦使用约会网站寻找约会对象。经过一段时间之后,她发现曾交往过三种类型的人:
- 1:不喜欢的人
- 2:魅力一般的人
- 3:极具魅力的人
她希望:
- 不喜欢的人则直接排除掉
- 工作日与魅力一般的人约会
- 周末与极具魅力的人约会
现在她收集到了一些约会网站未曾记录的数据信息,这更有助于匹配对象的归类。
开发流程
海伦把这些约会对象的数据存放在文本文件 datingTestSet2.txt 中,总共有 1000 行。海伦约会的对象主要包含以下 3 种特征:
Col1:每年获得的飞行常客里程数Col2:玩视频游戏所耗时间百分比Col3:每周消费的冰淇淋公升数
文本文件数据格式如下:
40920 8.326976 0.953952 3
14488 7.153469 1.673904 2
26052 1.441871 0.805124 1
75136 13.147394 0.428964 1
38344 1.669788 0.134296 1
读取数据
import matplotlib.pyplot as plt
import pandas as pd
data = pd.read_csv('datingTestSet2.txt',sep = '\t',header = None)
X = np.array(data.iloc[:,:-1])
y = np.array(data.iloc[:,-1])
切分数据
我们可以直接调用sklearn的函数将数据集切分为训练集和测试集
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
计算测试集数据和训练集间的距离,进行分类。
我们先用最简单的思想分类:将想要预测的样本,和训练集中每个样本的特征直接相减的绝对值之和作为距离,将距离最近的训练样本的标签标记为预测样本的标签。
class KNN:
def __init__(self):
pass
def train(self,X_train,y_train):
#读取训练集
self.X_train = np.array(X_train)
self.y_train = np.array(y_train)
def predict(self,X_test):
(m,d) = np.shape(X_test) #测试集的数量和特征数
y_pred = np.zeros((m)) #将预测的标签初始化为0
for i in range(m):
distance = np.sum(np.abs(self.Xtrain - X_test[i,:]),axis = 1) #求距离的绝对之和
min_index = np.argmin(distance) #找到最近点的索引
y_pred[i] = self.y_train[min_index] #将最近点的分类给新数据标记
return y_pred
我们可以将这个算法称为“最近邻算法“,直接取找最近的一个数据进行分类标记,我们将这个算法扩展到K近邻算法。
可以扩展的方向:
- 选择不同的距离公式
- 选择不同的K值
选择不同的距离公式:
上一个算法中用的距离公式为曼哈顿距离,将参数特征相减的绝对值求和,即L1距离。我们还可以用L2距离,
曼哈顿距离: d 1 ( I 1 , I 2 ) = ∑ P ∣ I 1 p − I 2 p ∣ d_1(I_1,I_2) = \sum_P|I_1^p - I_2^p| d1(I1,I2)=P∑∣I1p−I2p∣
欧式距离: d 2 ( I 1 , I 2 ) = ∑ P ( I 1 p − I 2 p ) 2 d_2(I_1,I_2) = \sum_P\sqrt{(I_1^p - I_2^p)^2} d2(I1,I2)=P∑(I1p−I2p)2
打个比方来说,当你搜索地图上的两个点,欧式距离就是将两个点用直线相连的空间距离;曼哈顿距离衡量的是你从A点开车到B点的距离,因为你不能穿过大楼和墙壁,所以衡量的是横向路线和纵向路线的的加总距离。
KNN算法中,欧式距离用的更多,因为我们一般衡量变量特征的在多维空间中的距离,这时候不需要“开车绕墙”。
如有兴趣,可自行学习其他距离公式,添加到我们后面的算法中。
选择不同的K值
我们不再是选取排序后距离最近的一个训练数据打标签,而是选择距离最近的前K个训练数据,找到大多数近邻归属的类别,将预测值归为此类。
排序和计数我们可以直接调用argsort函数和Counter函数
按照以上思想,我们重新改写KNN算法:
from collections import Counter
class KNN:
def __init__(self,k=1,metric ='euclidean'): #默认距离算法为欧式距离,默认最近邻
self.metric = metric
self.k = k
def train(self,X_train,y_train):
self.X_train = np.array(X_train)
self.y_train = np.array(y_train)
def predict(self,x_test):
(m,d) = np.shape(x)#测试集的数量和特征数
y_pred = np.zeros((m))#将预测的标签初始化为0
#============================= show me your code =======================
#============================= show me your code =======================
return ypred
可能你会问,如果两个分类刚好数量相等怎么办?可以有多种方法进行处理,如随机分类,如比较两类的距离总长度,我们这里不做更多处理,按Counter函数默认给出的分类。
选择K值
那么到底如何选择K值呢?我们可以选择在测试集中表现最好的K值。
本任务中直接调用sklearn中的kFold函数,将数据集进行k折验证,取每次验证的评分平均值作为此K值的误差评分。(这两个k表示的意思不一样,请留意)
如何定义测试结果的评分呢?可以直观地将分类正确的比例作为衡量指标。定义准确度的函数为:
def score(ypred,ytest):
return sum(ypred == ytest)/len(ytest)
将撰写的分类器中添加评分函数,这就是一个相对完整的分类器了,我们可以将他和sklearn的结果做比较
from collections import Counter
class KNN:
def __init__(self,k,metric ='euclidean'):
pass
self.metric = metric
self.k = k
def train(self,X,y):
self.X_train = np.array(X)
self.y_train = np.array(y)
def predict(self,x_test):
x = np.array(x_test)
(m,d) = np.shape(x)
ypred = np.zeros((m))
#============================= show me your code =======================
#============================= show me your code =======================
return ypred
def score(self,ypred,ytest):
return sum(ypred == ytest)/len(ytest)
和sklearn的KNeighborsClassifier算法做比较
#数据标准化
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
X_ = ss.fit(X)
X_std =ss.transform(X)
from sklearn.model_selection import cross_val_score
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsClassifier
k_range = range(1, 31)
k_error = []
#循环,取k=1到k=31,查看误差效果
for k in k_range:
knn = KNeighborsClassifier(n_neighbors=k)
#cv参数决定数据集划分比例,这里是按照5:1划分训练集和测试集
scores = cross_val_score(knn, X_std, y, cv=5, scoring='accuracy')
k_error.append(1 - scores.mean())
#画图,x轴为k值,y值为误差值
plt.plot(k_range, k_error)
plt.xlabel('Value of K for KNN')
plt.ylabel('Error')
plt.show()
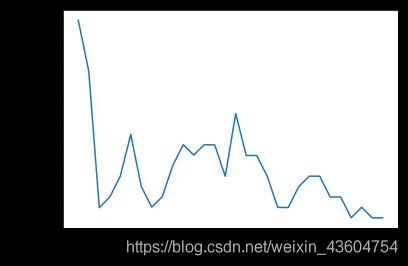
用撰写的K近邻算法测试数据,用同样的作图法输出每个K值的误差结果。
from sklearn.model_selection import KFold
kf = KFold(n_splits=5,shuffle=False) #将数据集分为互斥的5等份,用作测试
k_errors = [] #建立初始的误差列表
for k in k_range:
knn = KNN(k=k)
scores = []
for train , test in kf.split(X_std,y):
knn.train(X_std[train],y[train])
ypred = knn.predict(X_std[test])
score = knn.score(ypred,y[test])
scores.append(1-score)
k_errors.append(np.mean(scores))
plt.plot(k_range, k_errors)
plt.xlabel('Value of K for KNN')
plt.ylabel('Error')
plt.show()
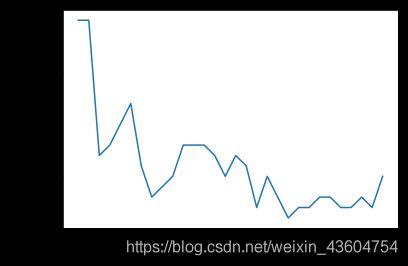
观察到,算法在k=21的时候表现良好,取K值为21,来预测一个新数据
knn = KNN(k=21)
knn.train(X_std,y)
# 定义类别对应的标签
resultList = ['不喜欢的人', '魅力一般的人', '极具魅力的人']
#输入数据
ffMiles = float(input("每年获得的飞行常客里程数?"))
percentTats = float(input("玩视频游戏所耗时间百分比?"))
iceCream = float(input("每周消费的冰淇淋公升数?"))
inArr = np.array([[ffMiles, percentTats, iceCream]])
#用之前的fit的标准化数据来转换数据
x_new = ss.transform(inArr)
#预测数据
ypred = knn.predict(x_new)
print("这个人属于: ", resultList[int(ypred) - 1])
每年获得的飞行常客里程数 38300
玩视频游戏所耗时间百分比 1.6
每周消费的冰淇淋公升数 .13
这个人属于: 不喜欢的人
参考资料
https://www.cnblogs.com/midiyu/p/10786765.html
https://www.cnblogs.com/listenfwind/p/10685192.html
https://blog.csdn.net/m0_38056893/article/details/102990001
http://people.csail.mit.edu/dsontag/courses/ml12/slides/lecture10.pdf
http://cs231n.github.io/classification/
https://www.csd.uwo.ca/courses/CS4442b/L3-ML-knn.pdf
http://cs231n.stanford.edu/slides/2019/cs231n_2019_lecture02.pdf
https://blog.csdn.net/FrankieHello/article/details/79659111
https://www.cnblogs.com/jyroy/p/9427977.html
https://baike.baidu.com/item/%E9%82%BB%E8%BF%91%E7%AE%97%E6%B3%95/1151153?fromtitle=knn&fromid=3479559&fr=aladdin