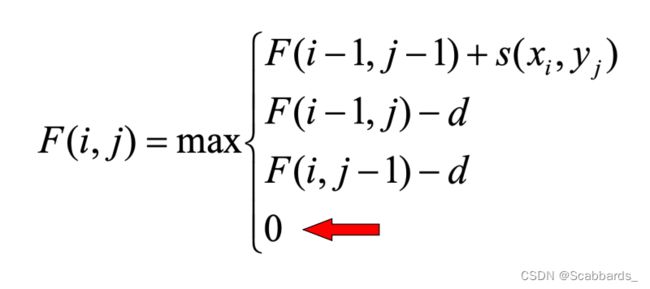INT102 笔记+例题(更新中）

整了点例题，推荐配合INT102 算法笔记_sanmusen_wu的博客-CSDN博客的笔记食用

欸嘿，主打一个题海战术，做到会为止

week1 伪代码与时间复杂度

伪代码（Pseudo Code）

题型1 展示循环中的每一轮

例1

选做1

选做2

题型2 修改代码

例1

题型 3 根据所给条件写代码

时间复杂度（Time complexity）

大小关系

例1 排序

 

 例2 证明

例4 循环证明

week2 评估基础查找与排序算法

线性查找（Linear Search）
二分法查找（Binary Search)
寻找连续子串出现位置 （Search for a pattern)
选择排序 （Selection Sort）

选择排序每次从未排序的部分中选择最小（或最大）的元素，然后将其放到已排序部分的末尾。在最坏情况下，选择排序需要进行 n*(n-1)/2 次比较。

冒泡排序（Bubble Sort）

冒泡排序是一种简单的排序算法，它通过相邻元素的比较和交换来将最大（或最小）的元素逐步“冒泡”到数列的末尾。在最坏情况下，冒泡排序需要进行 n*(n-1)/2 次比较，其中 n 是待排序序列的长度。

插入排序 （Insertion Sort Algorithm）选读

插入排序将待排序序列分为已排序和未排序两部分，每次将未排序部分的第一个元素插入到已排序部分的适当位置。在最坏情况下，插入排序需要进行 n*(n-1)/2 次比较。

快速排序（Quick Sort）

快速排序是一种高效的排序算法，它通过选取一个基准元素将序列分成左右两个子序列，然后对子序列进行递归排序。在最坏情况下，快速排序需要进行 n*(n-1)/2 次比较。

week3 分治思想和基础图论

分而治之（Divide and Conquer）*

步骤：

1）(Divide):将整个问题划分为多个子问题

2）递归求解（Conquer）：递归调用正在设计的算法求解每个子问题

3）合并（Combine）：合并子问题的解，形成原始问题的解

分析过程：

1）简历递归方程T(n）   T(n) = aT(n/b) +f(n)

2) 求解递归方程

可推↓

  例1？

  相信不止我一个人好奇这一步怎么来的.... 不过背下来就ok了

例2

例3?

 例4

例5

归并排序（Merge Sort）（O(nlogn)）

归并排序是一种稳定的排序算法，它采用分治的策略将序列分成较小的子序列，然后将子序列进行合并排序。在最坏情况下，归并排序需要进行 n*log(n) 次比较。

例1

 例2

很遗憾的是这个comparisons并不能像其他几种算法那样直接套公式，只能具体问题具体分析

基础图论
图（Graphs）

分类

simple graph 两个顶点最多一条边

multigraph 两个顶点多条边

pseudograph 允许自环

一些词汇

vertex 顶点

degree 度（degree）是用于描述图中顶点与边相关联的一个概念。

对于一个无向图，度指的是与一个顶点相连的边的数量。例如，如果一个顶点有3条边与其相连，则它的度为3。

而对于有向图，度分为入度（in-degree）和出度（out-degree），分别指的是指向一个顶点的边的数量和从一个顶点出发的边的数量。

adjcency

incidence

例1 

 adjacency：点到点是否有边

 

 incidence：按边来

 

 

树（Tree）
树的遍历

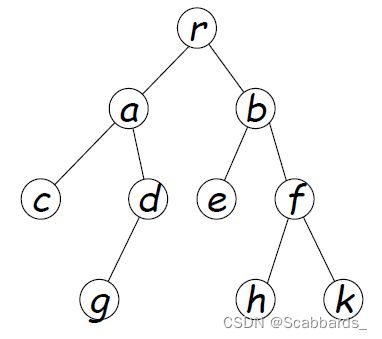
例1

 Preorder(前序）中左右

 inorder 中序 左中右

postorder 后序 左右中

例2

 前序

A - B - D - H - I - E - J - C - F - K - G

中序

H - D - I - B - E - J - A - F - K - C - G

后序

 H - I - D - J - E - B - K - F - G - C - A

欧拉回路（Euler circuit）

包含每条边的路径叫euler path，是回路的叫euler circuit

简单（simple）回路每一个边遍历至多一次，欧拉回路每一个边只能遍历一次

哈密顿图（Hamiltonian circuit / path）

设G是一个无向图。哈密顿回路(路径)是包含G的每个顶点恰好一次的回路(路径)。请注意，哈密顿电路或路径不会访问所有边。

week4 深度优先与广度优先

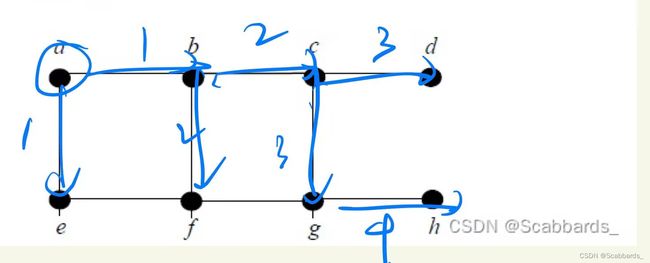
深度优先（Deep First Search)

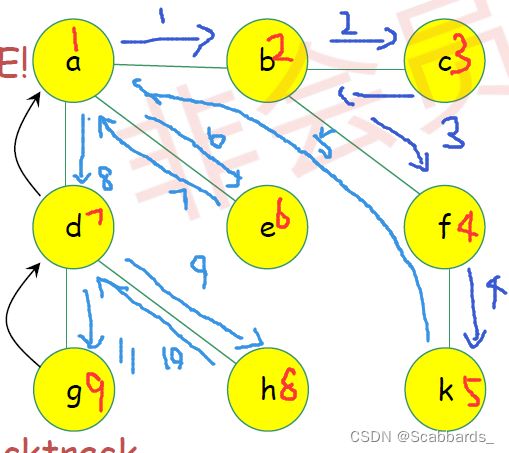
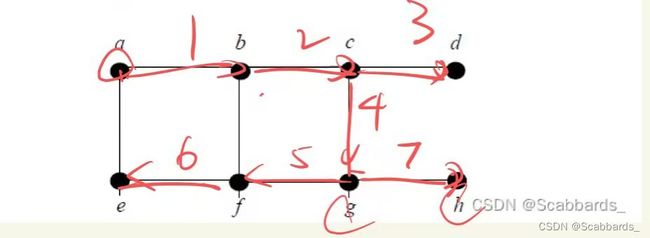
广度优先（Breadth First Search）

week5 贪心算法及最小生成树

贪心算法（Greedy Algorithms）
贪心背包问题（Knapsack Problem）
最小生成树（Minimum Spanning Tree)

简称 MST。给定一个带权的无向连通图， 如何选取一棵生成树，使树上所有边上权的总和为最小，这叫最小生成树

MST和SPT(shortest path tree)是完全不同的两个概念。SPT是source到
其他节点的距离，而MST是graph的一个属性，跟source无关。

最小生成树（MST）问题旨在找到一个连接所有图中顶点的树，使得树上的边权重之和最小。换句话说，MST是一个无环的连通子图，它包含了图中的所有顶点，并且边的权重之和最小。看的是全局最短路径。

最短路径树（SPT）问题则关注从一个源节点到图中其他所有节点的最短路径。我们可以把SPT看作是以源节点为根的一棵树，其中树中的边权重之和最小，覆盖了图中所有其他节点。看的是两个点间的最短路径。

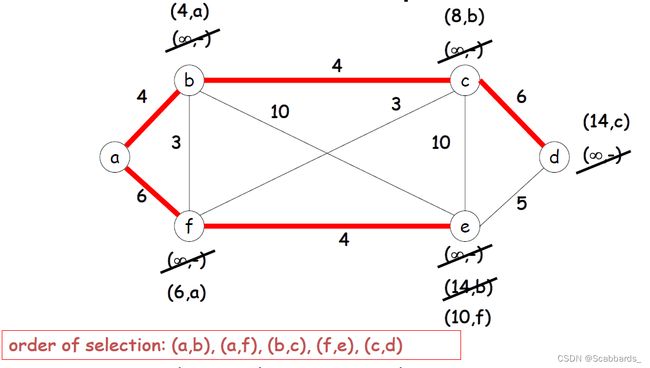
Prim's algorithm（ O(|E|*log|V|) ）

1.选取权值最小边的其中一个顶点作为起始点。
2.找到离当前顶点权值最小的边，并记录该顶点为已选择。
3.重复第二步，直到找到所有顶点，就找到了图的最小生成树。

例1

例2

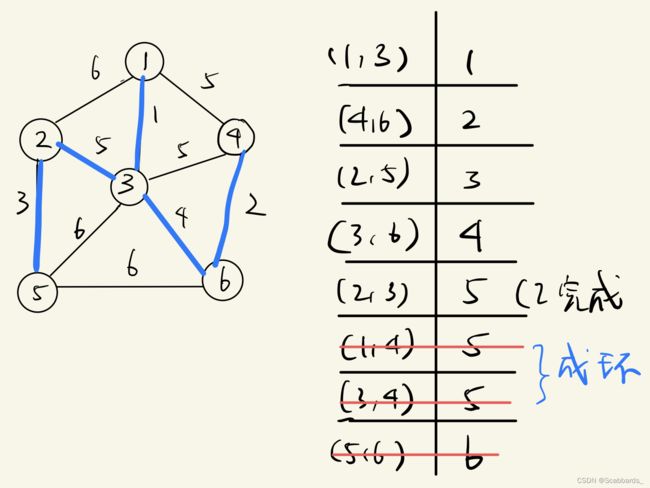
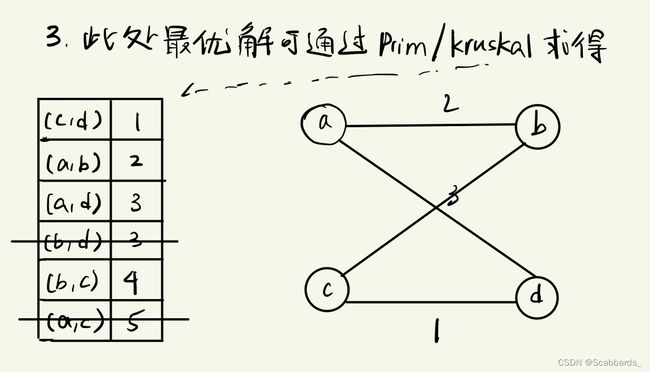
Kruskal's algorithm ( O(|E|*log|V|) ）

基本思想：按照权值从小到大的顺序选择 n-1 条边，并保证这 n-1 条边不构成回路
具体做法：首先构造一个只含 n 个顶点的森林，然后依权值从小到大从连通网中选择边加入到森林
中，并使森林中不产生回路，直至森林变成一棵树为止

例1

例2

例3

Dijkstra’s algorithm ( O(|E|*log|V|) )？

【算法】最短路径查找—Dijkstra算法_哔哩哔哩_bilibili

例1

 

 例2

 这是道综合例题

 Prim

Kruskal

 Dijskra

week6 动态规划

适合运用动态规划的问题：

1.子问题具有重叠性

2.有优化子结构

3.子问题往往不是相互独立的

斐波拉契（Fibonacci numbers）（O(n) )
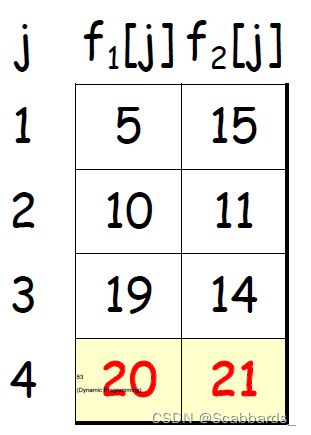
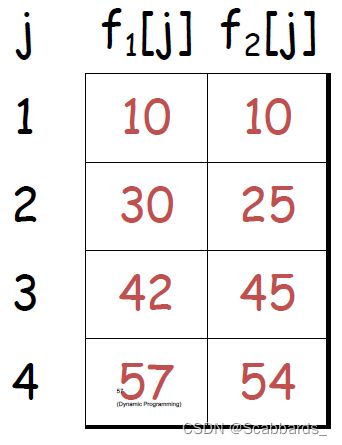
流水线调度（Assembly line scheduling）（O(nm^2^) )

为了使经过n个站的总时间最小，决定要去哪一站

例1

例2

 

week7 时空转换相关算法和图的最短路径

时空转换 （Space-for-time tradeoffs）
计数排序（Counting Sort）（O(n+k)）

排序算法：计数排序【图解+代码】_哔哩哔哩_bilibili

 元素之间没有比较

1. 首先，根据数列的范围设置多个桶，数列元素的范围为多少就设置几个桶。例如，待排序数列中只包含个位数，那么就设置从0~9十个桶。初始时桶内计数都为0。

2. 遍历原始数列，将遍历到的数对应的桶内计数自增1。

3. 遍历桶，更新每个桶的计数=这个桶的计数+前一个桶的计数。遍历结束后各个桶内计数既代表该桶对应元素在排序后数组中最后处于的位置

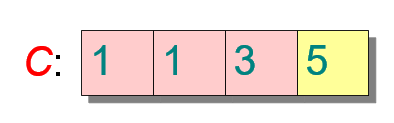
4. 从后向前遍历原始数列，将遍历的元素按照对应桶内的计数作为地址依次放在新数组中，然后该桶计数减1。遍历结束新数组就是排序后的数组

Q1

确认连续子串出现位置Horspool's Algorithm

是一种基于模式预处理的输入增强思想的简单字符串搜索算法，用于字符串匹配的算法，它的思路是基于字符不匹配时的"移位表"来跳过尽可能多的不必要比较。

-预处理模式以生成一个移位表，该表确定在不匹配发生时将模式移位多远

-总是基于文本的字符c与模式中的最后一个字符对齐，根据移位表的c项进行移位

这个教程说的超详细↓

horspool 1 从简单的例子开始_哔哩哔哩_bilibili

 shift数组计算

 Q1

图的最短路径
单起点最短路径（Single-source shortest paths)

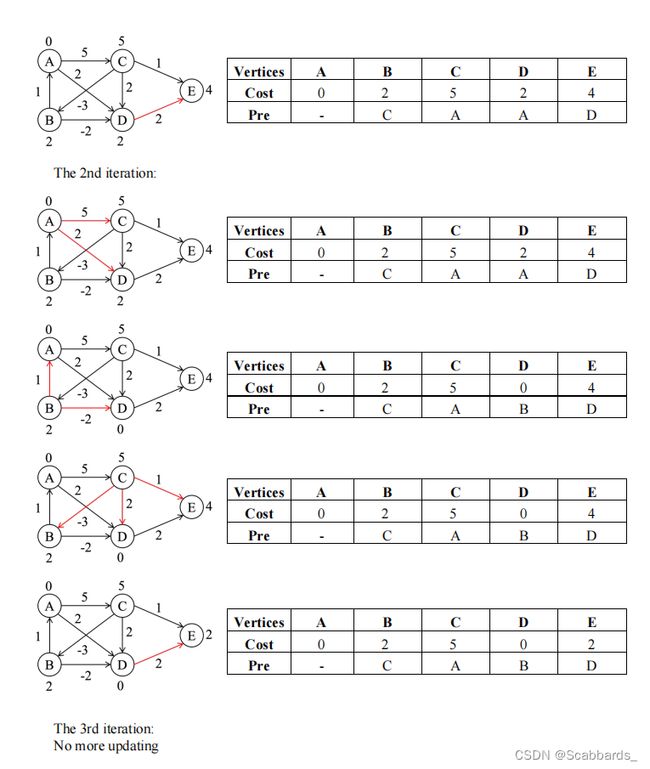
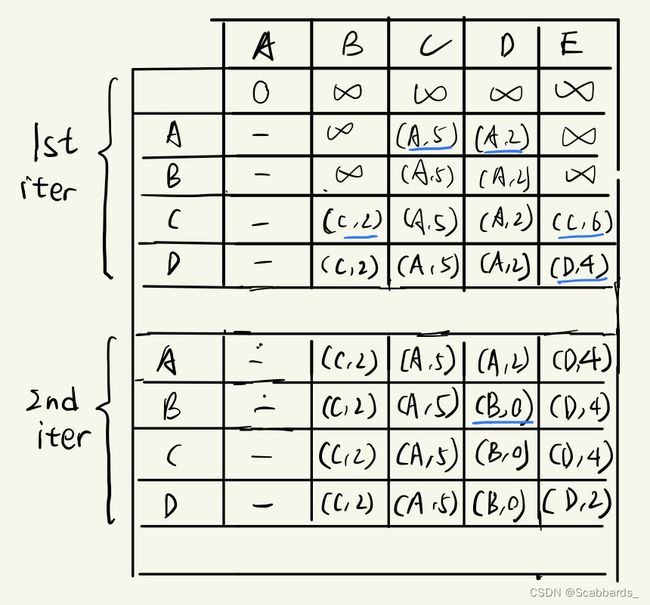
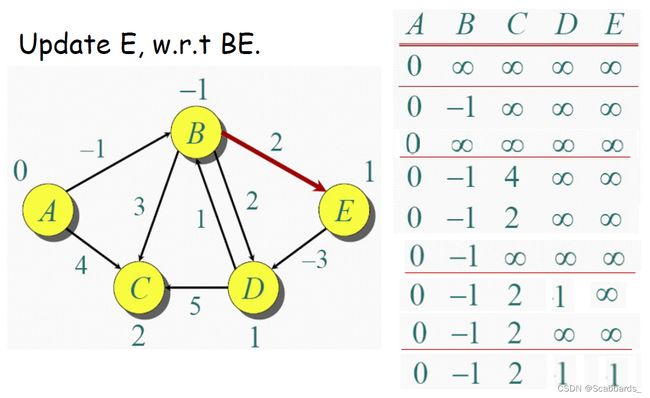
Bellman-Ford Algorithm

例1

例2

多源最短路径

Floyed Algorithom（All-pairs shortest paths）（O(n^3^))

又快又准做对考研真题，从考试的角度出发【弗洛伊德算法】【floyed】【多源最短路径】_哔哩哔哩_bilibili

算法的主要思想是动态规划(dp)

 例1

例2

构建传递闭包
Warshall’s Algorithm（O(n^3^))

week8 查找最长相同子序列

最长公共子序列问题（LCS Intuitive Solution）

 直接看视频就完事↓

最长公共子序列 - 动态规划 Longest Common Subsequence - Dynamic Programming_哔哩哔哩_bilibili

[轻松掌握动态规划]5.最长公共子序列 LCS_哔哩哔哩_bilibili

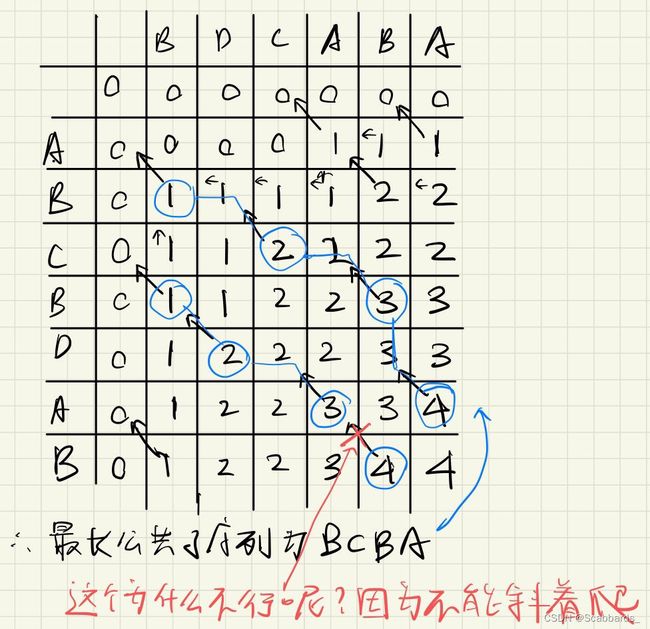
例1

​

例2

​

例3

爆算
dp
双序列比对问题（Pairwise Sequence Alignment Problem）

成对序列比对 Pairwise Sequence Alignment Problem

全局比对/局部比对dp（Global / Local alignment）

全局（global）

max（斜上方+分数，左/上 + 惩罚系数）

局部（local）

Q1

​

Global

 ​ 

​ 

Local

​​

 例2

Global

Local

例3

回溯dp的table

week 10 NP问题

谈谈计算机中的NP，NP-Hard，NP完全以及"NP=P？"问题_哔哩哔哩_bilibili

Circuit-SAT问题
范式（Normal form (NF)）
合取范式 (Conjunctive Normal Form)
析取范式 (Disjunctive Normal Form)
判断问题和最优化问题
判断问题（Decision problems）
最优化问题（Optimisation problems）
解决（solving）问题和判别（verifying）待定解
P和NP复杂类
P复杂类（Complexity Classes P ）
NP复杂类（Complexity Classes NP ）
多项式规约（Polynomial-time reduction）
NP-hard
NP-complete
NP=P?

week11 回溯剪枝DFS算法设计

精确解策略（Exact Solution Strategies）
算法设计（Algorithm Design Techniques）
[n皇后问题（n-Queens Problem）

https://leetcode-cn.com/problems/n-queens/

 

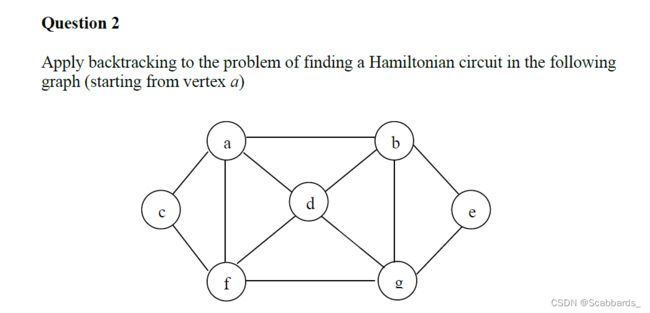
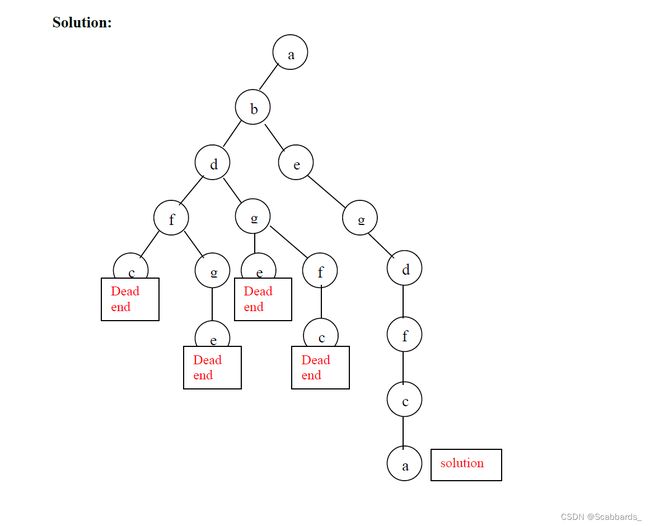
哈密顿电路（Hamiltonian Circuit ）

p.s以下每题的图并不是唯一的，不必纠结，a可以从b,c,d出发都行

例1

 

例2

N数之和问题（Subset-Sum Problem）

https://leetcode-cn.com/problems/4sum/

指派问题（Assignment Problem）

n项任务，对应n个人承担，应指派哪个人完成哪项任务，使完成效率最高

算法条件：

1. 目标函数求最小值

2. 人数和任务数相等

3. 效率非负

本质：

变换系数矩阵，找到n个不同行不同列的0元素，以求解指派问题最优解

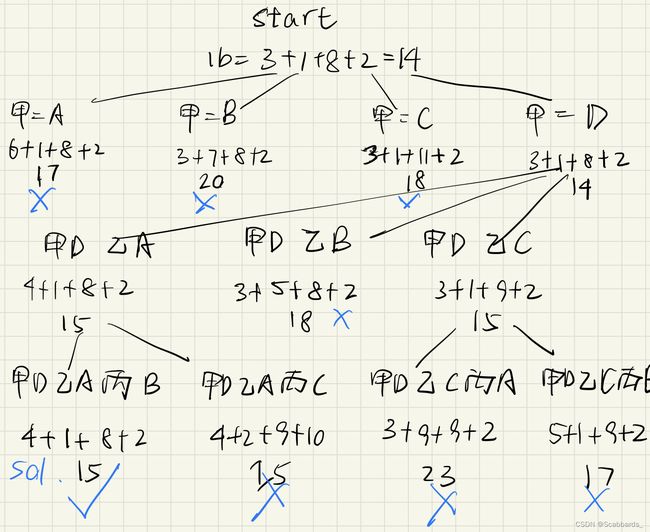
例1

例2

旅行商问题（Traveling Salesman Problem）

例1

例2

例3

 

week12 更多动态规划dp

一维动态规划问题 1-dimensional DP
目标和的加法式数量
贴砖 Troll Tiling
二维动态规划问题 2-dimensional DP
LCS Problem
间隔DP Interval DP
Tree DP
dp背包问题 Knapsack 0-1 Example

0/1背包问题-动态规划 Knapsack_problem Dynamic Programming_哔哩哔哩_bilibili

练习地址 https://alchemist-al.com/algorithms/knapsack-problem

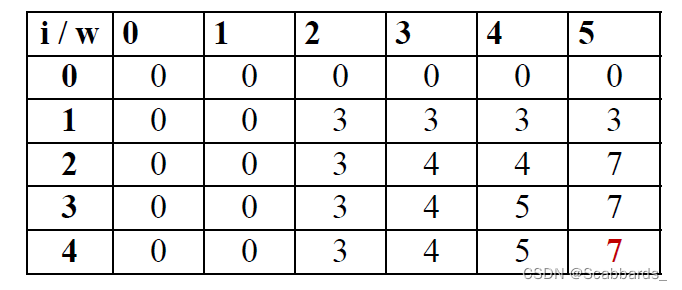
例1

 

 例2

sol

week13 近似求解

爆算 Brute-force algorithms
启发法 Heuristics
近似算法 Approximation algorithms
准确率Accuracy Ratio
c-approximation algorithm
近似解顶点覆盖问题VERTEX-COVER
近似解TSP问题
Nearest-neighbor
Euclidean instances
Multifragment-heuristic

把边按照距离从小到大排列，每次选择一个边加入集合，要求：

1. 新的边不会使集合内的任意一点出现三个度
2. 新的边不会使n-1之内的点形成环

比nearest-neighbor复杂，正确率相同

Twice-Around-the-Tree Algorithm

 1:构造图的最小生成树
(例如，通过Prim或Kruskal的算法)
阶段2:从任意顶点开始，创建一条绕树两圈并返回同一顶点的路径
阶段3:从阶段2中构造的电路创建一个巡回，通过创建快捷方式来避免多次访问中间顶点
注意:对于一般实例，RA =∞，但该算法往往比最近邻算法产生更好的行程

例1

 例2