K-近邻算法实现与应用(KNN)
文章目录
- 距离度量
- 曼哈顿距离
- 欧氏距离
- 最近邻算法
- K-近邻算法
- 算法实现
- 决策规则
- KNN算法实现
- 测试数据
- 丁香花分类
- 加载数据集
- 训练测试数据划分
- 训练模型
- 模型预测
- 准确率计算
- K 值选择
距离度量
曼哈顿距离
曼哈顿距离又称马氏距离,是计算距离最简单的方式之一。公式如下:
d m a n = ∑ i = 1 N ∣ X i − Y i ∣ d_{man}=\sum_{i=1}^{N}\left | X_{i}-Y_{i} \right |dman=i=1∑N∣Xi−Yi∣
其中:
- X XX, Y YY:两个数据点
- N NN:每个数据中有 N NN 个特征值
- X i X_{i}Xi :数据 X XX 的第 i ii 个特征值
公式表示为将两个数据 和 中每一个对应特征值之间差值的绝对值,再求和,便得到曼哈顿距离。
欧氏距离
欧式距离源自 N NN 维欧氏空间中两点之间的距离公式。表达式如下:
d e u c = ∑ i = 1 N ( X i − Y i ) 2 d_{euc}= \sqrt{\sum_{i=1}^{N}(X_{i}-Y_{i})^{2}}deuc=i=1∑N(Xi−Yi)2
- X XX, Y YY :两个数据点
- N NN:每个数据中有 N NN 个特征值
- X i X_{i}Xi :数据 X XX 的第 i ii 个特征值
公式表示为将两个数据 X XX 和 Y YY 中的每一个对应特征值之间差值的平方,再求和,最后开平方,便是欧式距离。
最近邻算法
介绍 K-近邻算法之前,首先说一说最近邻算法。最近邻算法(Nearest Neighbor,简称:NN),其针对未知类别数据 x xx,在训练集中找到与 x xx 最相似的训练样本 y yy,用 y yy 的样本对应的类别作为未知类别数据 x xx 的类别,从而达到分类的效果。
如上图所示,通过计算数据 X u X_{u}Xu (未知样本)和已知类别 ω 1 , ω 2 , ω 3 {\omega_{1},\omega_{2},\omega_{3}}ω1,ω2,ω3 (已知样本)之间的距离,判断 X u X_{u}Xu 与不同训练集的相似度,最终判断 X u X_{u}Xu 的类别。显然,这里将 绿色未知样本 类别判定与 红色已知样本 类别相同较为合适。
K-近邻算法
K-近邻(K-Nearest Neighbors,简称:KNN)算法是最近邻(NN)算法的一个推广,也是机器学习分类算法中最简单的方法之一。KNN 算法的核心思想和最近邻算法思想相似,都是通过寻找和未知样本相似的类别进行分类。但 NN 算法中只依赖 1 个样本进行决策,在分类时过于绝对,会造成分类效果差的情况,为解决 NN 算法的缺陷,KNN 算法采用 K 个相邻样本的方式共同决策未知样本的类别,这样在决策中容错率相对于 NN 算法就要高很多,分类效果也会更好。
算法实现
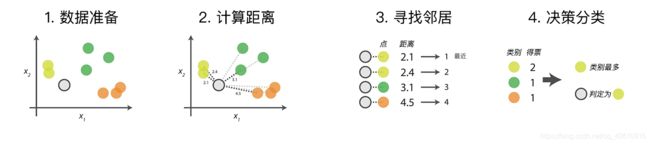
- 数据准备:通过数据清洗,数据处理,将每条数据整理成向量。
- 计算距离:计算测试数据与训练数据之间的距离。
- 寻找邻居:找到与测试数据距离最近的 K 个训练数据样本。
- 决策分类:根据决策规则,从 K 个邻居得到测试数据的类别。
决策规则
在得到测试样本和训练样本之间的相似度后,通过相似度的排名,可以得到每一个测试样本的 K 个相邻的训练样本,那如何通过 K 个邻居来判断测试样本的最终类别呢?可以根据数据特征对决策规则进行选取,不同的决策规则会产生不同的预测结果,最常用的决策规则是:
- 多数表决法:多数表决法类似于投票的过程,也就是在 K 个邻居中选择类别最多的种类作为测试样本的类别。
- 加权表决法:根据距离的远近,对近邻的投票进行加权,距离越近则权重越大,通过权重计算结果最大值的类为测试样本的类别。
KNN算法实现
def knn_regression(train_data, train_labels, test_data, k):
"""
参数:
train_data -- 训练数据特征 numpy.ndarray.2d
train_labels -- 训练数据目标 numpy.ndarray.1d
test_data -- 测试数据特征 numpy.ndarray.2d
k -- k 值
返回:
test_labels -- 测试数据目标 numpy.ndarray.1d
"""
### 代码开始 ### (≈ 10 行代码)
test_labels=np.array([])
for j in test_data: #
distances=np.array([])
for i in train_data: # 欧式距离
temp=np.sqrt(np.square(sum(j-i)))
distances=np.append(distances,temp)
sorted_labels=distances.argsort()
temp_label=train_labels[sorted_labels[:k]]
test_labels=np.append(test_labels, np.mean(temp_label))
### 代码结束 ###
return test_labels
测试数据
import numpy as np
# 训练样本特征
train_data = np.array([[1, 1], [2, 2], [3, 3], [4, 4], [5, 5],
[6, 6], [7, 7], [8, 8], [9, 9], [10, 10]])
# 训练样本目标值
train_labels = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
# 测试样本特征
test_data = np.array([[1.2, 1.3], [3.7, 3.5], [5.5, 6.2], [7.1, 7.9]])
# 测试样本目标值
knn_regression(train_data, train_labels, test_data, k=3)
输出:array([2., 4., 6., 7.])
丁香花分类
加载数据集
import pandas as pd
import matplotlib.pyplot as plt
lilac_data = pd.read_csv(
'https://labfile.oss.aliyuncs.com/courses/1081/course-9-syringa.csv')
lilac_data.head() # 预览前 5 行
训练测试数据划分
from sklearn.model_selection import train_test_split X_train,X_test, y_train, y_test
=train_test_split(train_data,train_target,test_size=0.4, random_state=0)
X_train,X_test,y_train,y_test分别表示,切分后的特征的训练集,特征的测试集,标签的训练集,标签的测试集;其中特征和标签的值是一一对应的。train_data,train_target分别表示为待划分的特征集和待划分的标签集。test_size:测试样本所占比例。random_state:随机数种子,在需要重复实验时,保证在随机数种子一样时能得到一组一样的随机数。
from sklearn.model_selection import train_test_split
# 得到 lilac 数据集中 feature 的全部序列: sepal_length,sepal_width,petal_length,petal_width
feature_data = lilac_data.iloc[:, :-1]
label_data = lilac_data["labels"] # 得到 lilac 数据集中 label 的序列
X_train, X_test, y_train, y_test = train_test_split(
feature_data, label_data, test_size=0.3, random_state=2)
X_test # 输出 lilac_test 查看
训练模型
sklearn.neighbors.KNeighborsClassifier((n_neighbors=5,weights=‘uniform’,algorithm=‘auto’)
n_neighbors:k值,表示邻近个数,默认为5。weights: 决策规则选择,多数表决或加权表决,可用参数('uniform','distance')algorithm: 搜索算法选择(auto,kd_tree,ball_tree),包括逐一搜索,kd树搜索或ball树搜索
from sklearn.neighbors import KNeighborsClassifier
def sklearn_classify(train_data, label_data, test_data, k_num):
# 使用 sklearn 构建 KNN 预测模型
knn = KNeighborsClassifier(n_neighbors=k_num)
# 训练数据集
knn.fit(train_data, label_data)
# 预测
predict_label = knn.predict(test_data)
# 返回预测值
return predict_label
模型预测
# 使用测试数据进行预测
y_predict = sklearn_classify(X_train, y_train, X_test, 3)
y_predict
准确率计算
def get_accuracy(test_labels, pred_labels):
# 准确率计算函数
correct = np.sum(test_labels == pred_labels) # 计算预测正确的数据个数
n = len(test_labels) # 总测试集数据个数
accur = correct/n
return accur
get_accuracy(y_test, y_predict)
K 值选择
当 K 值选取为 3 时,可以看到准确率不高,分类效果不太理想。 K 值的选取一直都是一个热门的话题,至今也没有得到很好的解决方法,根据经验,K 值的选择最好不超过样本数量的平方根。所以可以通过遍历的方式选择合适的 K 值。以下我们从 2 到 10 中画出每一个 K 值的准确率从而获得最佳 K 值。
normal_accuracy = [] # 建立一个空的准确率列表
k_value = range(2, 11)
for k in k_value:
y_predict = sklearn_classify(X_train, y_train, X_test, k)
accuracy = get_accuracy(y_test, y_predict)
normal_accuracy.append(accuracy)
plt.xlabel("k")
plt.ylabel("accuracy")
new_ticks = np.linspace(0.6, 0.9, 10) # 设定 y 轴显示,从 0.6 到 0.9
plt.yticks(new_ticks)
plt.plot(k_value, normal_accuracy, c='r')
plt.grid(True) # 给画布增加网格

从图像中可以得到,当 K=4 和 K=6 时,模型准确率相当。但机器学习选择最优模型时,我们一般会考虑到模型的泛化能力,所以这里选择 K=4,也就是更简单的模型。
文章来源:【机器学习】K-近邻算法实现与应用(KNN)_ccql's Blog-CSDN博客_k近邻算法应用