【论文阅读笔记】Edge-Preserving Decompositions for Multi-Scale Tone and Detail Manipulation

论文小结：

  本文提出了一种可以多尺度提取边缘保留的多尺度图像解耦技术，同时作者表明基于双边滤波的细节解耦技术，在任何尺度上都达不到满意的结果，都是受限的。作者提出的方法是以带权重的最小二乘优化法为框架的，它特别适合图像的渐进式平滑化和多尺度细节提取。

  实际上，本文提出的方法WLS，是一种比BLF效果更好的保边算法，但耗时也要大得多。

论文介绍

  作者认为，双边滤波非常适合去躁和精细尺度上的细节提取。但作者认为其不太合适任意尺度的细节提取，而任意尺度的细节提取对于多尺度解耦是必要的。比如，为了减少HDR图像的动态范围，通常对基础层进行非线性压缩映射，然后与（可能衰减或增强的）细节层重新组合[Pattanaik et al. 1998; Tumblin and Turk 1999; Durand and Dorsey 2002]。Fattal et al. [2007]采用了相似的过程来增强形状和细节，除了他们的重点是增强和/或组合来自多个来源的细节层，而不是压缩整体动态范围。

  在增强的时候，图像被分为基础层和细节层。计算基础层是一个图像粗话过程，必须小心地进行粗化，以避免在单独操作基础层和细节层并重新组合后可能出现的伪影。 [Schlick 1994; Tumblin and Turk 1999; Li et al. 2005]等研究员认为这些伪影是由于将信号分解为基础和细节分量时引入的失真引起的。如下图所示，粗化图像中边缘的模糊和锐化都会导致细节层出现振铃，随后可能表现为光晕和梯度反转。因此，线性过滤和硬分割都不适合计算基本细节分解，研究人员转向了边缘保留过滤器，它提供了这两个极端之间的折衷。

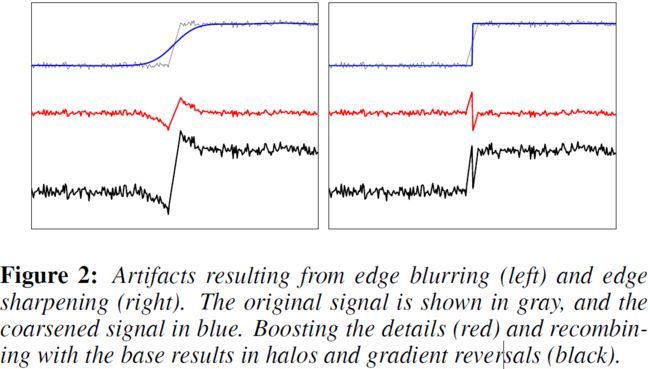
  理想的边缘保留滤波器必须既不模糊也不锐化分离粗尺度图像特征的边缘，同时平滑这些边缘之间的区域。 不幸的是，这样的算子并不存在，因为通常不可能明确地确定应该保留哪些边缘。 此外，为了产生多尺度的基础细节分解，运算符必须允许越来越大的图像特征从基础层迁移到细节层。 换句话说，它必须让越来越大的区域变得越来越平滑。

  作者认为，虽然 BLF 在平滑强度的微小变化同时保留强边缘方面非常有效，但它实现渐进粗化的能力相当有限。如下图所示，左上角是合成示例，拥有几个不同步长幅度的边缘，并且包含两个不同尺度的噪声。为了更清楚的看对比，作者使用彩色图（右上角）来哦可视化图像强度。

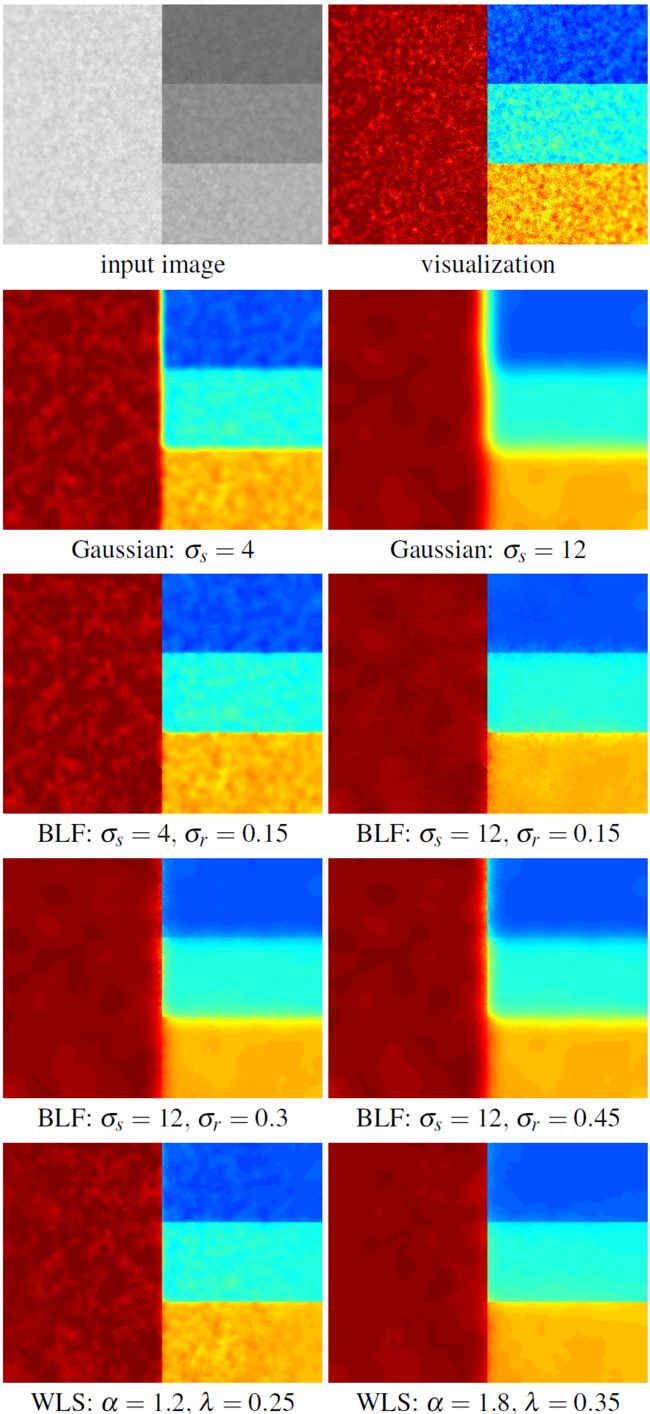
  从上图第二行可以看到使用线性高斯滤波器对图像进行滤波的结果。使用小尺度的空间核（${\sigma }_s=4$）可以去除细粒度的噪声，较大尺度的空间核（${\sigma }_s=12$）可以去除较大尺度的噪声。但也如预期的那样，边缘会变得模糊。为了保证边缘的平滑，人们希望保留边缘，同时在由这些边缘界定的区域中实现类似程度的平滑。

  从上图第三行左，可以看到，使用较小的${\sigma }_s=4$，可以消除大部分细粒度噪声，同时保持大部分边缘清晰。若仅加大${\sigma }_s$来消除大尺度噪声，能取得的进展不大，同时可以看到细粒度噪声又在某些边缘附近重新引入回来了，如上图第三行右所示。

  因此，单纯增加${\sigma }_s$并不能实现更好的平滑，必须还得增加范围支持${\sigma }_r$。但是，增加${\sigma }_r$会削弱双边滤波保护边缘的能力，甚至会引入一些模糊，如上图3第四行所示：在(${\sigma }_r\to \infty$)的约束时，双边滤波会变成一个高斯滤波。

  第三四行展示了双边滤波在边缘保护能力和平滑能力之间是进行权衡的。随着提取细节的比例增加，双边滤波倾向于模糊更多边缘，这可能会产生光晕伪影。相比之下，对同一图像使用WLS平滑，可以实现更精细和更粗糙的平滑，同时保留阶跃边缘，并且不会引入明显的伪像，如上图最后一行。

  可以通过迭代应用双边滤波实现更强的平滑，这样做的基础是在每次迭代时减少${\sigma }_r$。然而，这个过程产生的结果类似于使用均值平移滤波，它趋向于过度锐化强边缘，因此导致强边缘周围的小特征保留在了粗糙图像中。

WLS实现边缘保留平滑

  边缘保留平滑可被视为两个可能相互矛盾目标的折中：给定一张图$g$，想要目标图$u$，其特征是在显著梯度上与$g$相近，而其他地方尽可能平滑。形式上，这可被表示为寻找最小值：$$\sum _p((u_p-g_p{)}^2+\lambda (a_{x,p}(g)(\frac{\partial u}{\partial x}{)}_p^2+a_{y,p}(g)(\frac{\partial u}{\partial y}{)}_p^2))\text{\hspace{1em}(3)}$$  其中$p$是指定像素的空间位置，$a_{x,p}$和$a_{y,p}$是平滑度权重。公式（3）的第二项（正则项）是通过最小化u的偏导数来实现平滑。这样的目标函数，是为了保持强边缘，平滑噪声。平滑度权重$a_{x,p}$和$a_{y,p}$以空间变化的方式强制执行平滑度要求。用矩阵符号的形式，公式（3）可以由下公式表达：$$(u-g{)}^T(u-g)+\lambda (u^T{D}_x^T{A}_x{D}_{x}u+u^T{D}_y^T{A}_y{D}_{y}u)\text{\hspace{1em}(4)}$$  其中，$A_x$和$A_y$是包含平滑权重$a_x(g)$和$a_y(g)$的对角矩阵，$D_x$和$D_y$是离散微分算子。

  最小化公式（4）的向量$u$有唯一线性解：$$(I+\lambda L_g)u=g\text{\hspace{1em}(5)}$$  其中$L_g=D_x^T{A}_x{D}_{x}u+D_y^T{A}_y{D}_{y}u$

  省略公式推导和细节，因为该算法速度不快，暂时应用不上。

多尺度边缘保留分解

  假设图像$g$，目标是构建$k+1$级分解，$u_1,...,u_k$是$g$的各级粗糙版本，以$u_k$作为基础层$b$，$k$个细节层可以被定义为$$d_i=u_{i-1}-u_i，其中i=1,...,k，u_0=g$$

  很容易推理出来，g可以从基础层和细节层中恢复：$$g=b+\sum _{i=1}^k{d}_i$$

  有两种方法可以得到逐级粗糙序列$u_1,...,u_k$。

  方法一是使用公式（5）$k$次，每次使用不断增大的的$\lambda$参数，作者发现这种方法分解的结果很适合HDR压缩和多尺度细节增强（使用$\alpha \in [1.2,1.4]$），如下图的左列。$$u_{i+1}=F_{c^i\lambda }(g)\text{\hspace{1em}(13)}$$

  方法二是将每次的操作进行迭代，即在模糊图上进行进一步模糊。这种方法中，图像被反复平滑，类似于均值漂移滤波和多尺度双边变换，由此产生的粗化图像更强烈地倾向由强边缘分段恒定区域，如上图的右列。在每次迭代中，同样增加$\lambda$以产生更平滑的效果。作者发现这种迭代方案更合适丢弃或削弱某些细节的应用程序，比如图像抽象(使用$\alpha =1.8$或者$2.0$)。$$u_{i+1}=F_{c^i\lambda }(u_i)\text{\hspace{1em}(14)}$$

结果对比

  将基于WSL的多尺度分解和之前的其他方案进行对比。

  如上面所述，为了通过双边滤波实现逐进粗化，有必要同时增加${\sigma }_s$和${\sigma }_r$。之前也有人做过相关工作，比如Chen [2007]使用双边金字塔来进行渐进式视频抽象。虽然这种策略会产生更平滑的区域，但它也可能导致强边缘明显模糊。
  使用图像的一维部分来演示了这一点，下图$5$的一维信号左半部分是一个较大的特征，右半部分是一个小的（狭窄的）特征。蓝色曲线显示了输入信号逐步粗化的结果。
（1）使用双边滤波（左图），大特征和小特征都逐渐变得更平滑，从而在相应的细节信号中产生振铃现象（下图$5$红色曲线所示）。
（2）使用WLS，相同的边缘会被逐渐被腐蚀，但不会显著地扭曲信号的形状。而且，使用WLS时，围绕着边缘的小特征要比大特征要腐蚀地更快，这会导致小特征迁移到细节（detail）层，而不会出现明显的振铃，即使周围边缘很强。
（3）Fattal [2007]提出了另一种渐进粗化策略，是对前一张模糊图进行双边滤波获得的逐级粗化序列。在每次迭代中${\sigma }_r$逐渐减少，以确保在前一级别中保留的边缘在下一级别中仍会保留。该策略如下图的右边所示，它虽然避免了平滑强边缘，但一些小区域（在精细层中围绕边缘周围的）可能永远不会迁移到任何细节（datail）层。因此，细节层操作无法移除、抑制或强调此类细节。 另一个问题是边缘过度锐化，这可能会导致薄的梯度反转伪影（请注意图 5 中的细尖峰和图 10 中的像素宽光晕）。

  下图$6$展示了上述两种策略测行为。（1）在双边金字塔（左列）中，一些强边缘在粗化过程中“坍塌”，在细节层引入可见的振铃。与上面图$4$底行中的基础细节进行对比，图$4$更一致地保留了强边缘。如前所述，细节层中的振铃可能会在操作层并将它们重新组合在一起的应用程序中导致光环伪影。（2）Tumblin [1999] 提出的 LCIS方法对检查产生的分解也很有启发性；（3）Choudhury [2003] 解决了LCIS和BLF公邮的一些缺点。（2）和（3）的两种方法，随着粗化的进行，强边缘和坍塌，而在剩余的强边缘周围，细节层中会出现明显的振铃。（对比图$4$看振铃现象会比较明显）

  上述的光环伪影的表现在Durand [2002]的色调映射算法也有体现，比如他们有时会产生细微但可见的光晕。但基于WLS的分解应用想用的算法产生的结果不会有任何的可见光晕，同时保留了良好的局部对比度（如下图$7$所示）。

  如果细节层得到显著提升，光晕伪影会更加突出，下图$8$显示了一个光晕伪影的示例。基于BLF的细节层（顶部）会导致沿着高对比度边缘出现伪影，而当分解是基于WLS（底部）时，这些伪影是不存在的。在每个图像的右侧部分，中等比例的细节都得到了增强，使用BLF完成时一会产生光晕。

应用和结果

  作者使用本文的多尺度边缘保留分解实现了很多简单的工具（简单地实现），比如摄影色调调整（tone manipulation），HDR色调映射（tone mapping），细节增强和图像抽象。

  本文使用公式(5)求解，该解算器的性能和像素数量呈线性关系，在CPU 2.2 GHz Intel Core 2 Duo 上每百万像素大约需要 3.5 秒。Buatois. [2007]描述了一个更通用的求解器，使用GPU实现，加速了3.2倍。

多尺度色调映射

  本文实现了一个简单的交互式工具，用于在不同比例下操纵细节的色调和对比度。
  给定一张图片，作者首先将其分解为三个层次的分解：在CIELAB亮度通道上，分为粗糙基础层次$b$，以及两个细节层次$d^1$，$d^2$。分解是通过公式（13）那种非迭代的方式完成的，即每次都是在原图上进行的。然后向用户呈现一组滑块，用于控制基础层的曝光$\eta$，基础层的曝光增强因子${\delta }_0$，细节层的增强因子${\delta }_1,{\delta }_2$。映射的结果$\hat{g}$在每个像素点$p$表示如下：$${\hat{g}}_p=\mu +S({\delta }_0,\eta b_p-\mu )+S({\delta }_1,d_p^1)+S({\delta }_2,d_p^2)\text{\hspace{1em}(16)}$$

  其中，$\mu$是亮度范围内的均值，$S$是一个 sigmoid 曲线$S(a,x)=\frac{1}{1+exp(-ax)}$，近似移动和归一化。sigmoid的目标是避免当细节层被显著提升时会发生的硬裁剪（hard clip）。$S({\delta }_0,\eta b_p-u)$这项是为了控制基础层的曝光和对比度，而其余项控制中等和精细尺度细节的增强。需要知道的是，当分解计算完毕，公式(16)能实时评估（这意思是分解的耗时不算，这就能实时）。

  作者发现这个简单的工具可以非常有效地控制不同对比下的局部对比度。该方式的有效操作范围非常广泛，通常需要非常极端的操作才能导致伪影出现。比如上面的图像$1$、图像$8$和下面的图像$9$都是使用$\alpha =1.2$，$\lambda =0.1$用于细粒度滤波，$\alpha =1.4$，$\lambda =0.4$用于中等尺度滤波。作者发现三个金字塔级别足以满足他们所实验过的图像，使用更多级别可以实现更精细的控制，但也需要用户操纵更多滑块。

细节增强

  本文的分解方法也可以用来代替Fattal[2007]使用的基于BLF的多尺度分解，用于多光图像集合的形状和细节增强。
  本文的实验显示：在令人反感的伪影出现之前，本文的分解允许人们比Fattal的方法进一步增强和夸大细节。下图$10$上显示了两种方法增强效果的对比：Fattal使用BLF的方法会导致沿着边缘位置出现一个像素宽的梯度反转，这可能是由于这些边缘在分解过程中过度锐化所致。对比而言，本文提出方法的结果边缘看起来更干净。同时，作者证明了本文方法可以从单个输入图像（而不是Fattal等人使用的三个多光图像）生成高度夸张的细节。

HDR色调映射

  本文的分解很容易被用来执行HDR图像的细节保留压缩。比如将Durand的色调映射算法中的BLF替换为基于WLS的平滑，可以避免有时在其结果中可见的轻微光晕伪像（上图$8$）。

  本文实验的另一种色调映射算法选择是Tumblin提出的，但将其基于LCI的多尺度分解替换为本文提出的基于WLS的分解。具体来说，对亮度通道进行4层级分解（一个基础层，三个细节层），将每个级别乘以某个因子比例，并重建一个新的对数亮度通道。

  上图$11$显示了两种方式生成的两个色调映射结果。（1）在最左边的图像中，我们的目标是获得一个具有夸张局部对比度的相当平坦的图像（与 LCIS 在该图像上产生的典型结果相似，但更极端）。这是通过强烈压缩基础并提升精细比例细节层来实现的。（2）在最右边的图像中，我们追求的是更像照片的外观，但高光部分的深度比 Reinhard 的运算符 [2002] 更深。 我们通过使用较少的基础压缩和适度提升较粗糙的细节层来实现这一结果。

渐进式图像抽象

  图像抽象的表现入下图所示。